Тема 3. Сравнение двух выборных средних арифметических по критерию Стьюдента

Цель работы: научиться рассчитывать критерий Стьюдента и, сравнивая его с постоянной величиной, делать вывод и определять причины достоверных и не достоверных различий между двумя выборочными средними арифметическими

Теоретические знания

Традиционные задания по физической культуре, спорту и реабилитации сложились таким образом, что в их основе лежат идеи выборочного метода. Основное сводится к тому, что исследованию подлежит генеральная совокупность не в полном составе, а своей репрезентативной частью – выборочной совокупностью.

Что касается объёма выборки, то согласно основных положений математичской статистики, выборка тем репрезентативнее, чем она полнее. В каждом конкретном случае количество объектов, что отбираются в выборку, определяется индивидуально.

Основная задача выборочного метода состоит в определении двух показателей – среднего арифметического значения () и среднего квадратического отклонения ().

В практике спорта прийнято выбирать надёжность Р = 0,95 и соответствующий ей уровень значимости L = 0,05, отражающий основную группу исследуемых задач. В отдельных случаях, при необходимости быстрого увеличения, надёжность принимается Р = 0,99 и L = 0,01.

Большинство задач выборочного метода класифицируются как сравнительные. Сравниваются две и более выборочные совокупности. При сравнении устанавливается принадлежность этих выборок к одной и той же генеральной совокупности. Это имеет значение при определении достоверности различий между двумя выборочными средними арифметическими.

Таким образом, при работе с выборочным методом в практике физической культуры, спорта и реабилитации, при изучении небольшого количества исследованных можно найти основные среднестатистические показатели большой группы, а также определить, существенна ли разница между несколькими однотипными группами объектов.

С помощью выборочного метода математической статистики можно оценить:

1. Эффективность учебно-воспитательного, учебно-тренировочного, оздоровительного или реабилитационного процесса.

2. Какая из двух сравниваемых групп лучше (какой из двух исследуемых лучший) по:

- уровню развития физических качеств (быстроты, силы, выносливости, гибкости, ловкости);

- уровню подготовленности (физической, технической, тактической и …);

- состоянию здоровья;

- физическому развитию;

- состоянию системы организма (сердечно-сосудистой, дыхательной и…)…

Примечание: если сравниваются показатели двух исследуемых, то относительно каждого проводится несколько измерений (до 10-ти).

3. Преимущество или идентичность методики:

-обучения двигательным умениям и навыкам;

-развития физическим качествам;

-повышения уровня подготовленности;

-оздоровления;

-реабилитационных мероприятий и …

Выборочный метод математической статистики позволяет сравнивать показатели:

1. Двух групп.

2. Двух спортсменов; лиц, не занимающихся спортом; лиц разных медициских групп (основная, подготовительная и специальная).

3. У одной группы (одного человека) в начале и по окончании учебно-тренировочного, учебно-воспитательного, оздоровительного или реабилитационного процесса.

Примечание: продолжительность процесса зависит от того, через какое время будут иметь место изменения в исследуемых показателях.

Для определения достоверности различий между выборочными средними арифметическими необходимо обработать числа обеих сравниваемых выборок способом вариационных рядов, то есть определить среднее арифметическое значение ( и ), среднее квадратическое отклонение (_х и _у) и ошибку среднего арифметического значения (m_x и m _y).

Достоверность и не достоверность различий определяется при сравнении критерия Стьюдента (t) и постоянной величины (tгр).

Критерий Стьюдента определяется по формуле:

t =	/ – /
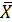	√ mx2 +m y2

t – критерий Стьюдента;

, – среднее арифметическое значение первой и второй выборки;

m_x, m _y – ошибка среднего арифметического значения первой и второй выборки.

Примечание: ошибка среднего арифметического значения (случайная ошибка) имеет так же название – ошибка репрезентативности.

Репрезентативность – выводы, сделанные на выборке можно перенести на всю генеральную совокупность.

Постоянная (граничная) величина (tгр) находится по специальной таблице критерия Стьюдента (смотри таблицу 1), для соответствующей надёжности и объёма выборки.

Чтобы определить t_гр по таблице, необходимо знать k- число степеней свободы, которое рассчитывается по формуле:

1. k = N_x + N_y – 2, если N_x ≠ N_y , δ_х = δ_y или δ_х ≠ δ_y

2. k = 2N – 2, если N_x = N_y, δ_х ≠ δ_y

При сравнении t и t_гр определяется достоверность различий между двумя выборочными средними арифметическими:

1. Если t ≥ t_гр - различия между сравниваемыми выборочными средними арифметическими достоверна (не случайна), существенна и объясняется влиянием определённых факторов.

Причины достоверных различий:

а) лучше одна из групп (один из исследумых);

б) при сравнении двух методик, одна эффективнее, чем другая;

в) при сравнении условий проведения занятий, проводимых по одной методике, одни условия лучше, чем другие;

г) эффективно построенный учебно-тренировочный, учебно-воспитательный, реабилитационный или оздоровительный процесс.

Примечание: для определения лучшей группы, человека (если сравниваются двое людей по одному показателю), методики, условий, необходимо сравнить среднее арифметическое значение первой и второй выборки (,).

2.Если t < t_гр - различия между сравниваемыми выборочными средними арифметическими не достоверны (случайна) и объясняются влиянием случайных факторов.

Причины не достоверных различий:

а) не правильный подбор группы;

б) недостаточная численность выборки;

в) одинаковые показатели обеих групп (двух исследуемых);

г) при сравнении двух методик – методики идентичны (одинаковы);

д) при сравнении условий проведения занятий по одной методике, условия однаковы;

є) не эффективно построенный учебно-тренировочный, учебно-воспитательный, реабилитационный или оздоровительный процесс.

Примечание: при сравнении среднего арифметичческого значения первой и второй выборки (,), они равны или незначительно отличаются.

Рассмотрим тему на примере:

Для специальностей «Физическое воспитание» и «Физическая реабилитация»

В 2-х группах спортсменов, занимающихся плаванием (Xi и Yi) измерили разность ЧСС, уд/мин (разница ЧСС - измерение ЧСС после максимально быстрого прохождения дистанции и в состоянии относительного покоя). Установить, достоверны ли различия по показателю ЧСС в исследуемых группах и в чём их причина

Xі 92 94 95 97 99 100 ni 3 4 7 2 1 2 Yі 98 102 103 104 105 ni 3 5 6 1 2	Nx = 19 Nx = 17
Ход работы:

1. Определяем среднее арифметическое значение 2-х выборок (,) по формуле взвешенного среднего арифметического, так как не все варианты встречаются по одному разу:

=(уд/мин)

(уд/мин)

2.Определяем дисперсию 2-х выборок (Dх, Dу)

3. Для дальнейшей работы строим таблицу

а) Для показателей первой выборки

і	ni		()2	()2 ni
92	3	- 4	16	48
94	4	- 2	4	16
95	7	- 1	1	7
97	2	1	1	2
99	1	3	9	9
100	2	4	16	32
				114

б) Для показателей второй выборки

Yi	ni		()2	()2 ni
98	3	84	16	48
102	5	0	0	0
103	6	1	1	6
104	1	2	4	4
105	2	3	9	18
				76

3. Определяем среднее квадратическое отклонение 2-х выборок (_х,_у)

δ_х = √Д_х δ_х = √6,3 = 2,5

δ_y = √Д_y δ_y = √ 4,75 = 2,18

4. Определяем ошибку среднего арифметического значения 2-х выборок (m_x, m_y)

N < 20, т.к. m =	δ
	√ N -1

mx =	2,5	=	2,5	= 0,58
	√ 19-1		√ 18

my =	2,18	=	2,18	=	2,18	= 0,55
	√ 17-1		√ 16		4

5. Определяем критерий Стьюдента ( t ).

t =	/ – /
	√ mx2 +m y2

t =	/96-102/	=	/-6/	=	6	= 7,5
	√0,582 + 0,552		√0,3364 + 0,3025		0,8

1. Определяем число степеней свободы (k)

k = N_x + N_y -2, т.к. N_x ≠ N_y (19 ≠ 17) и δ_х ≠ δ_y (2,52 ≠ 2,18)

k = 19 + 17 – 2 = 36 – 2 = 34

При k = 34, t_гр = 2,04 (смотри таблицу) при надёжности Р = 0,95

Р = 0,95 – на 95% полученным результатам и сделанным выводам можно доверять.

7. Сравниваем t и t_гр

t > t_гр (7,5 > 2,04) – различия между показателями разницы ЧСС двух групп спортсменов, занимающихся плаваньем достоверны (не случайны).

Вывод: t > t_гр (7,5 > 2,04) – различия между двумя группами спортсменов, занимающихся плаваньем, по показателю разницы ЧСС, достоверны (не случайны) и объясняются лучшей подготовленностью и более високим функциональным состоянием сердечно-сосудистой системы первой группы, потому что < (96 <102).

Примечание

Таблиця 1. Граничное значение критерия Стьюдента (t_гр)

Надёжность Р = 0,95, k – число степеней свободы

k	tгр	k	tгр
1	12,71	18	2,10
2	4,3	19	2,09
3	3,18	20	2,09
4	2,78	21	2,08
5	2,57	22	2,07
6	2,45	23	2,07
7	2,36	24	2,06
8	2,31	25	2,06
9	2,26	26	2,06
10	2,71	27	2,10
11	2,20	28	2,05
12	2,18	29	2,05
13	2,16	30	2,04
14	2,14	40	2,02
15	2,13	60	2,00
16	2,12	120	1,98
17	2,11	∞	1,96