
Приклади розвязування задач
Знайдіть координати вектора
 в базисі
в базисі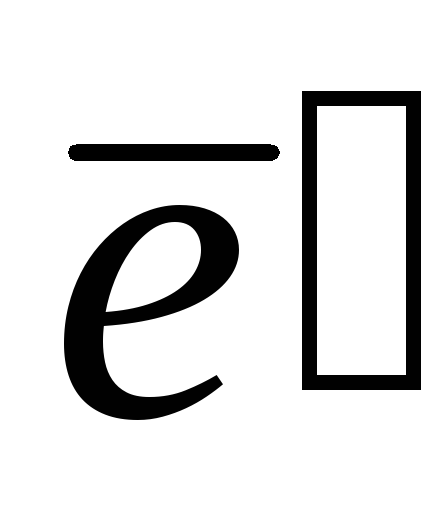 ,
якщо він заданий в базисі
,
якщо він заданий в базисі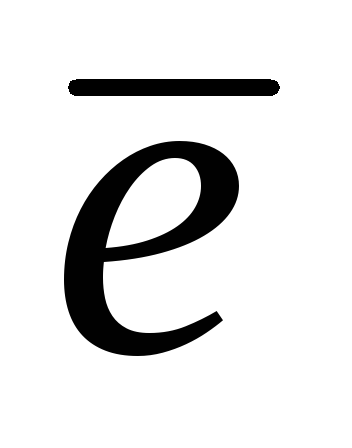 :
:
![]() .
.
Розвязання:
Нехай
![]() – координати вектора
– координати вектора![]() в базисі
в базисі![]() .
Складемо матрицю переходу від базису
.
Складемо матрицю переходу від базису![]() до базису
до базису![]() :
:
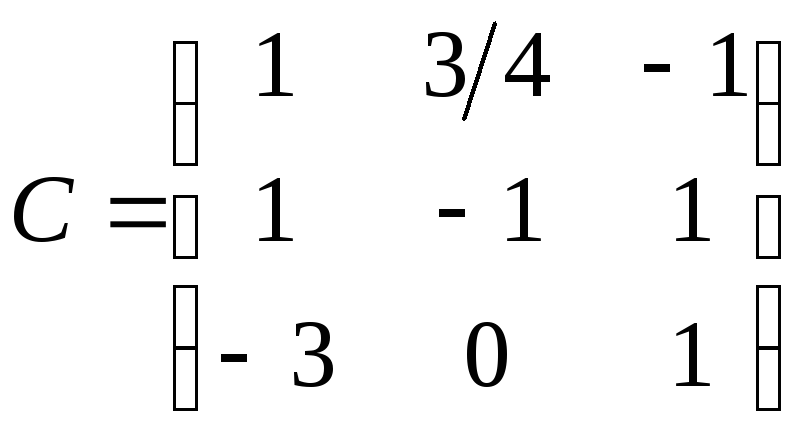 .
.
Тоді координати
вектора
![]() в базисі
в базисі![]() можна визначитиз
матричного рівняння:
можна визначитиз
матричного рівняння:
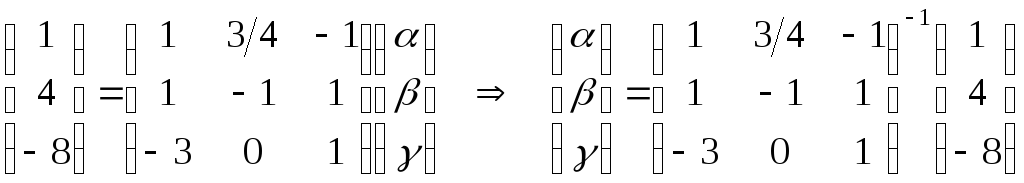 .
.
Надаємо читачеві можливість самостійно переконатися в тому, що
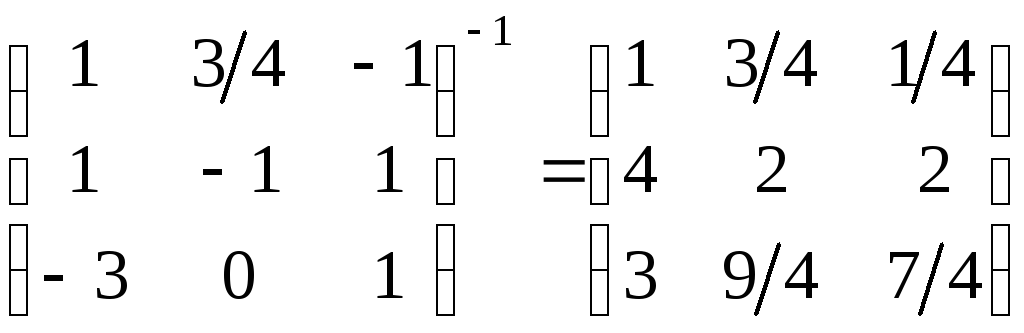 .
.
Тому координати
вектора
![]() в новому базисі набувають вигляду:
в новому базисі набувають вигляду:
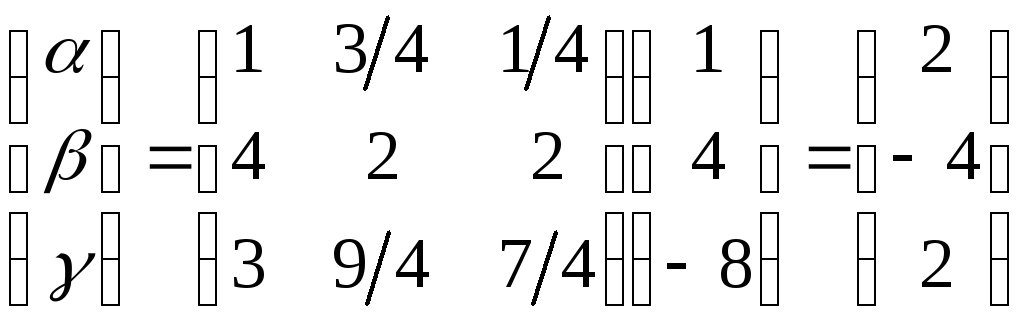 .
.
Нехай
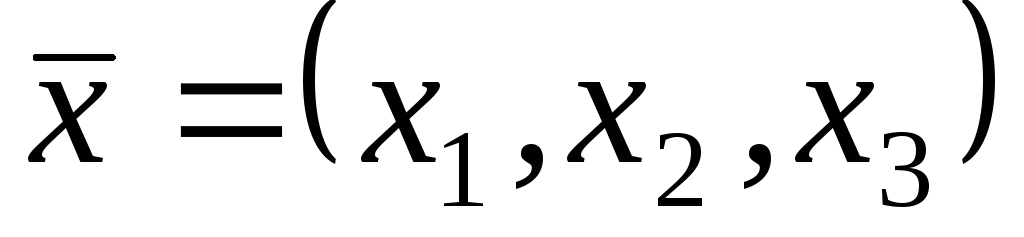 .
Перевірте, чиє
лінійним перетворення
.
Перевірте, чиє
лінійним перетворення
 .
.
Розвязання:
Нехай
вектори
![]() та
та![]() мають координати
мають координати![]() і
і![]() відповідно. Перевіримо виконання
властивостей лінійного перетворення
для довільних векторів
відповідно. Перевіримо виконання
властивостей лінійного перетворення
для довільних векторів![]() ,
,![]() :
:
![]()
![]()
![]()
З іншого боку:
![]()
![]()
![]() .
.
Оскільки
взагальномувипадку![]() ,
то
,
то![]() ідане перетворення неєлінійним.
ідане перетворення неєлінійним.
Нехай
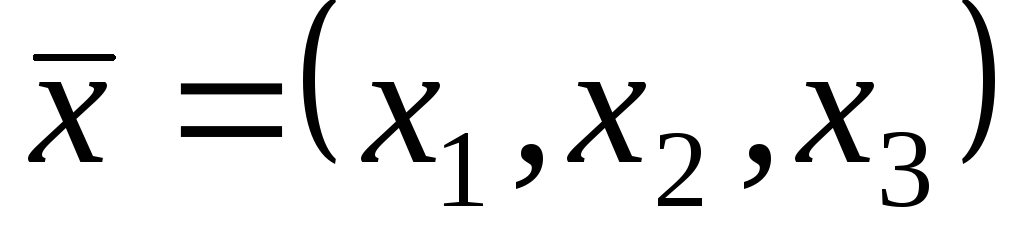 ,
,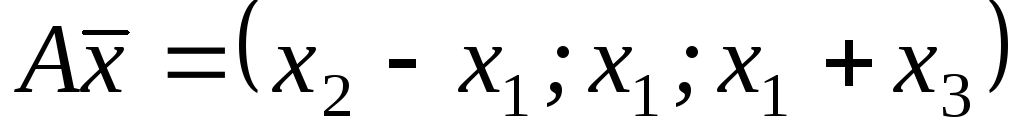 ,
,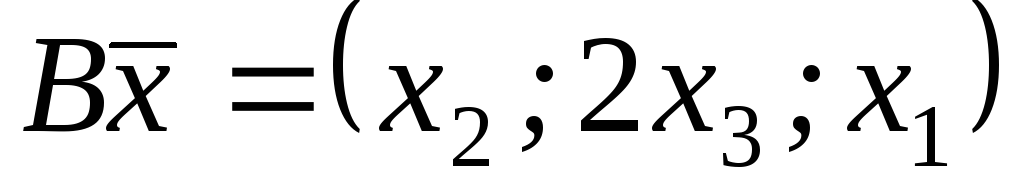 .
Знайдіть
.
Знайдіть
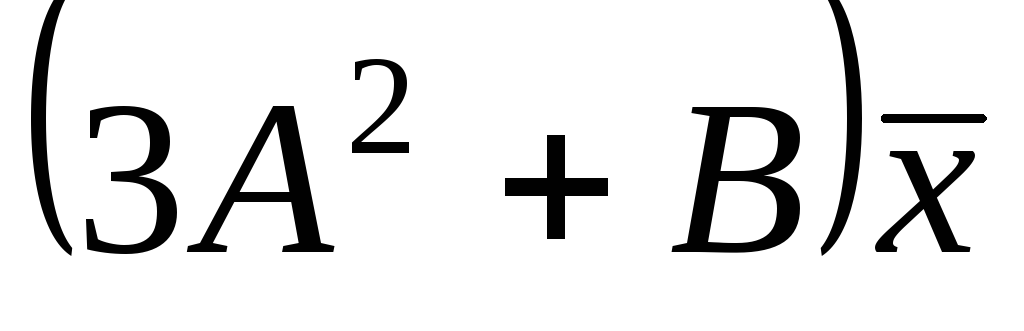 .
.
Розвязання:
I
спосіб.
За умовою
![]() ,
тоді
,
тоді
![]()
![]()
![]() .
.
Оскільки
відображення
![]() є
лінійним (читачеві не складе труднощів
переконатися в цьому самостійно), то
є
лінійним (читачеві не складе труднощів
переконатися в цьому самостійно), то
![]() .
.
Тому
![]()
![]() .
.
IIспосіб. Знайдемо елементи
матриць лінійних перетворень
![]() і
і![]() .
Для цього знайдемо образи базисних
векторів:
.
Для цього знайдемо образи базисних
векторів:
![]()
Розташуємо
їх по стовпцях та отримаємо матриці
перетворень
![]() і
і![]() :
:
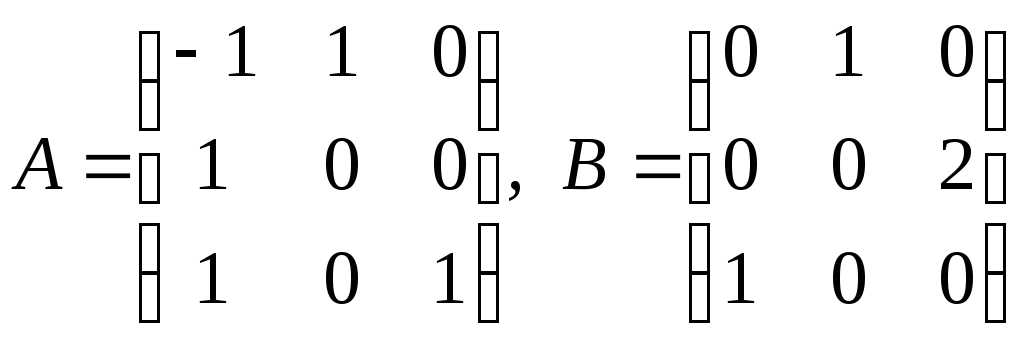 .
.
Тоді:
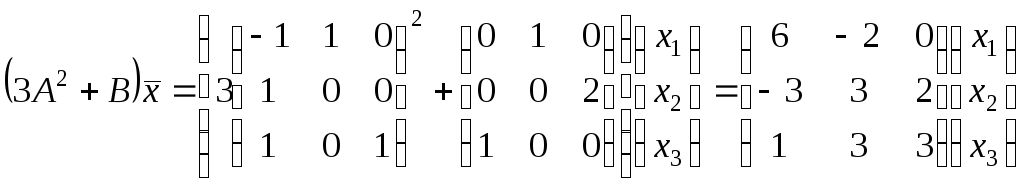
або
![]() .
.
Знайдіть матрицю оператора
 в базисі
в базисі
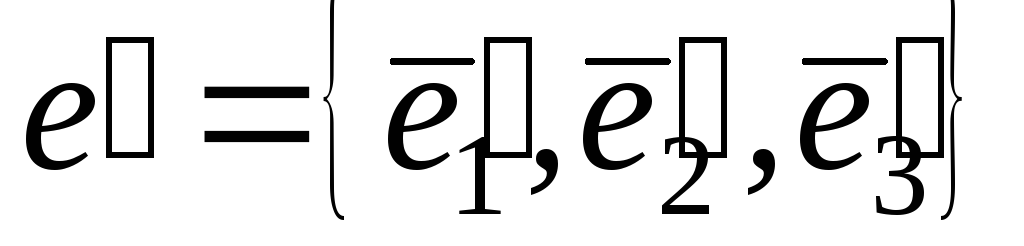 ,
де
,
де
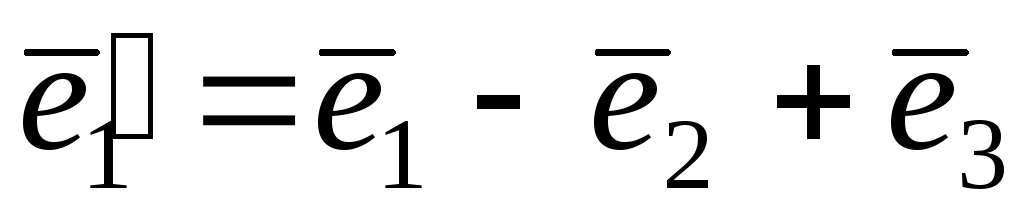 ,
,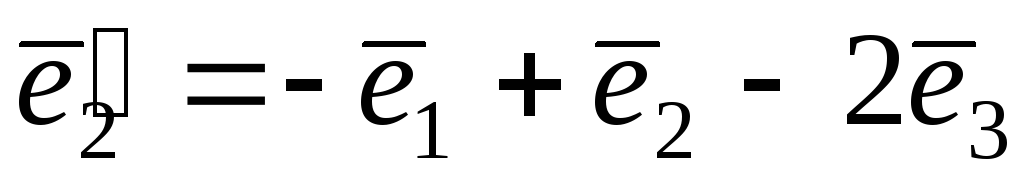 ,
,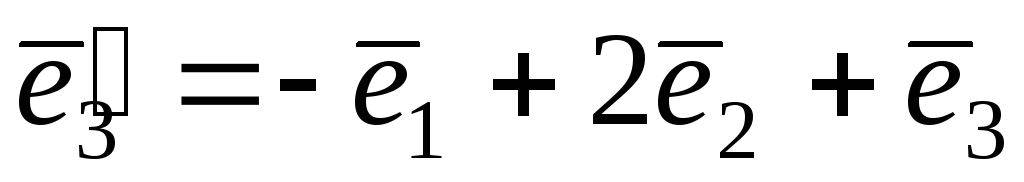 ,
якщо вона задана в базисі
,
якщо вона задана в базисі
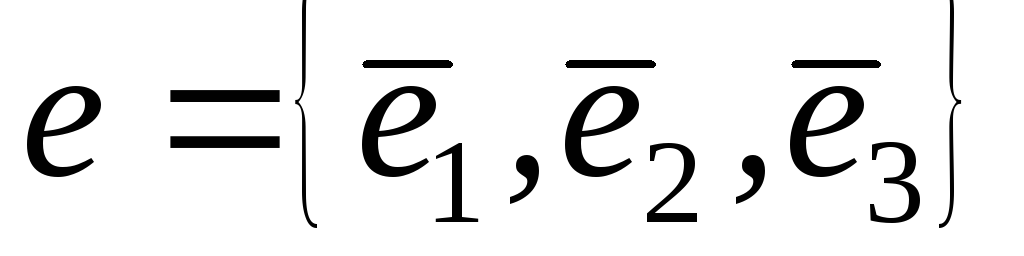 :
:
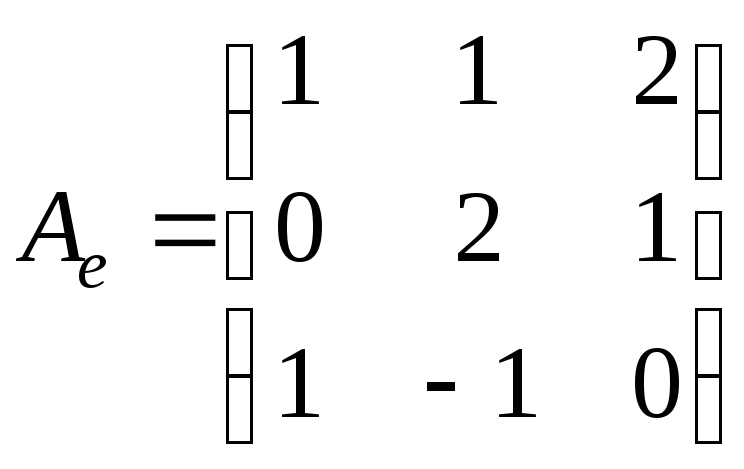 .
.
Розвязання:
Знайдемо елементи
матриці в новому базисі за
формулою
![]() ,
де
,
де
![]() – матриця переходу від базиса
– матриця переходу від базиса![]() до
до![]() :
:
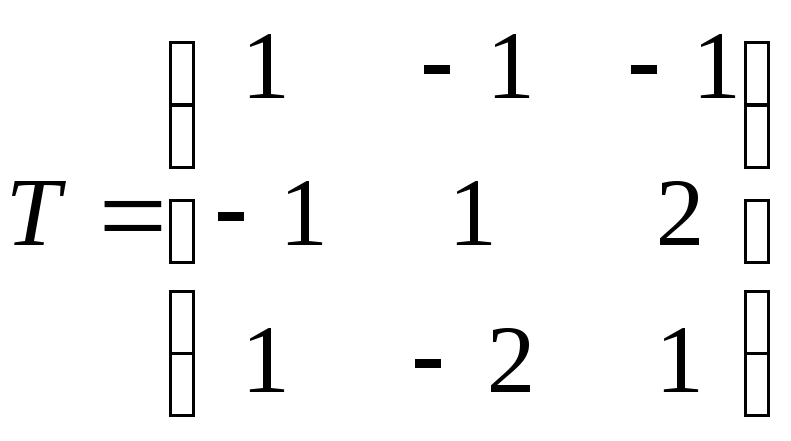 ,
,
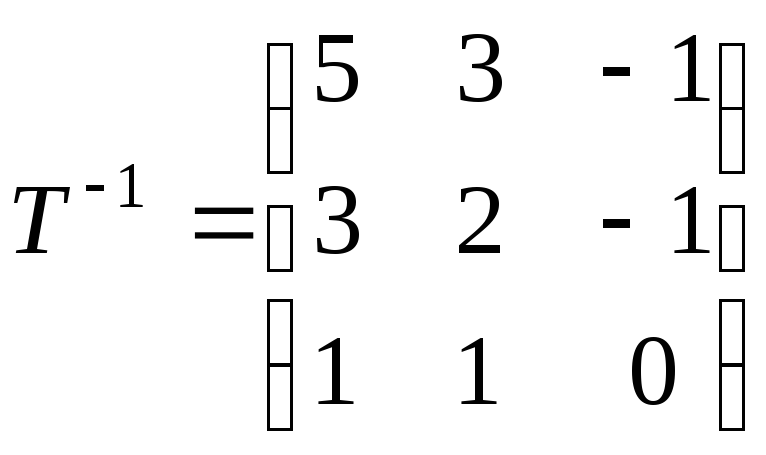 .
.
Тоді
 .
.
Доведіть лінійність, знайдіть матрицю, область значень і ядро оператора повороту щодо осі
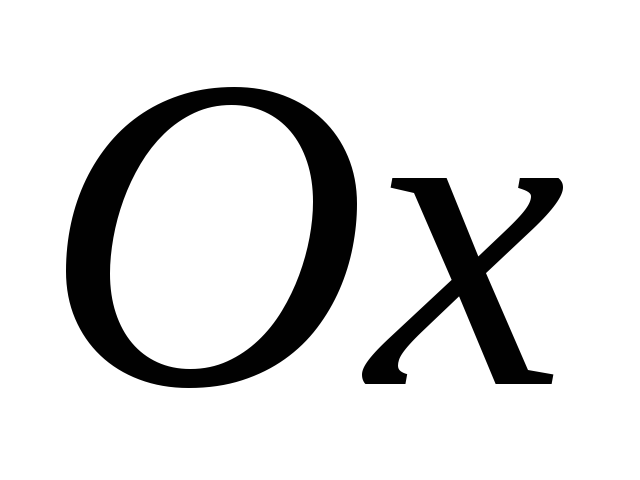 на кут
на кут
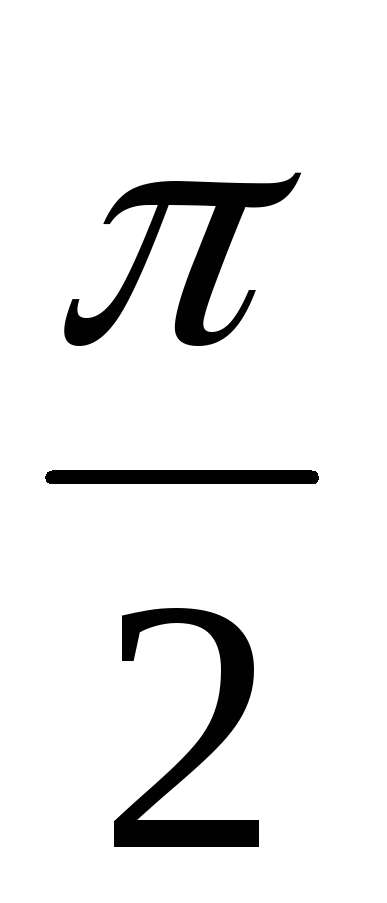 вдодатному
напрямку.
вдодатному
напрямку.
Рішення|розв'язання|:
Даному операторові відповідає перетворення, яке, очевидно, є лінійним.
Для знаходження
матриці оператора
![]() знайдемообрази
базисних векторів:
знайдемообрази
базисних векторів:
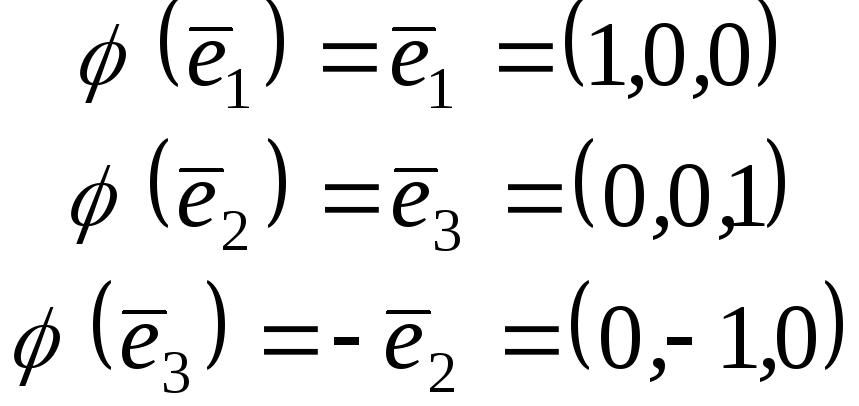
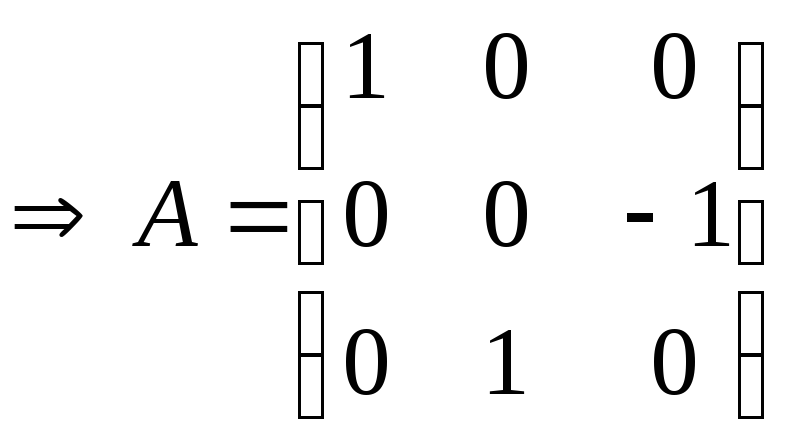 .
.
Для знаходження ядра оператора необхідно вирішити|рішати| рівняння :
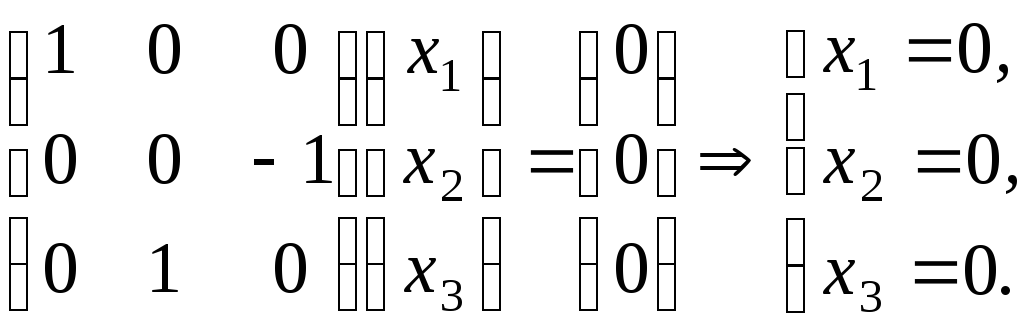
Таким чином,, а значить . Відома формула . Звідси .
Знайдіть власні значення і власні вектори матриці
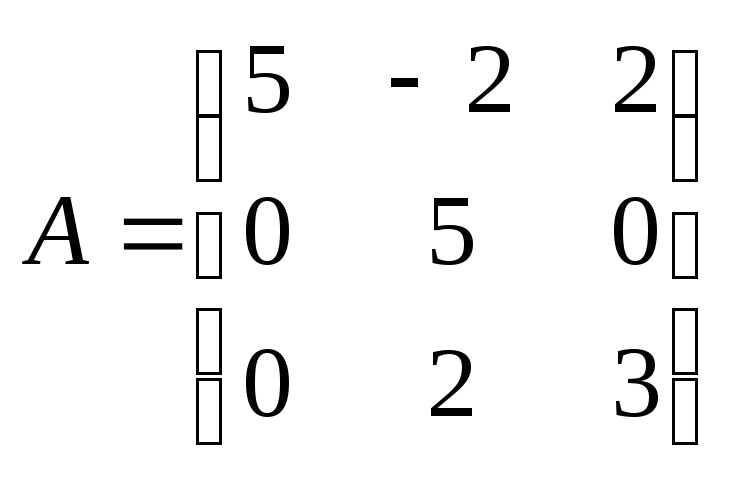 .
.
Рішення|розв'язання|:
Складемо характеристичне рівняння матриці :
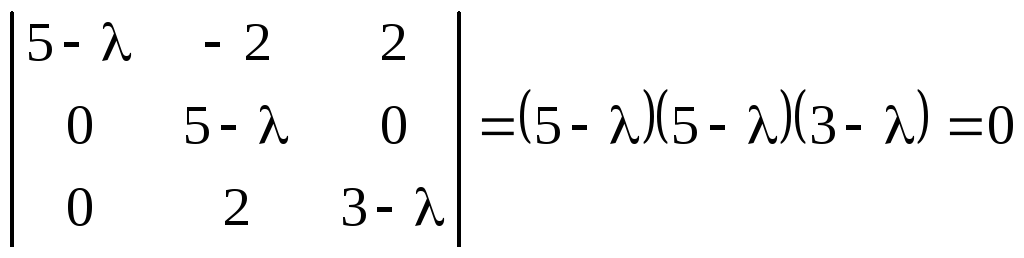 .
.
Значить, – власні значення матриці .
Власні вектори знайдемо з|із| рівняння .
При
Власні вектори, відповідні, мають вигляд|вид|
![]()
![]() .
.
При
Власні вектори, відповідні мають вигляд|вид|
![]() ,
,
![]() .
.
З'ясуєте, чи можна привести матрицю оператора до діагонального вигляду|виду|шляхом переходу до нового базису.У разі|в разі|позитивної відповіді знайдіть цей базис і відповідний вид матриці.
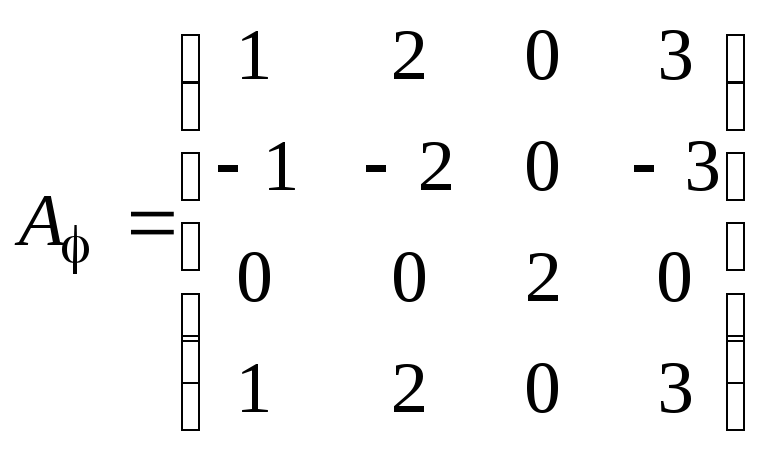 .
.
Рішення|розв'язання|:
Знайдемо власні значення матриці, а так само їх алгебра кратності:
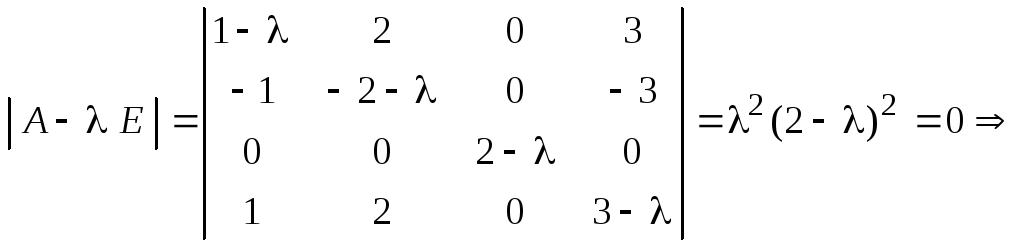
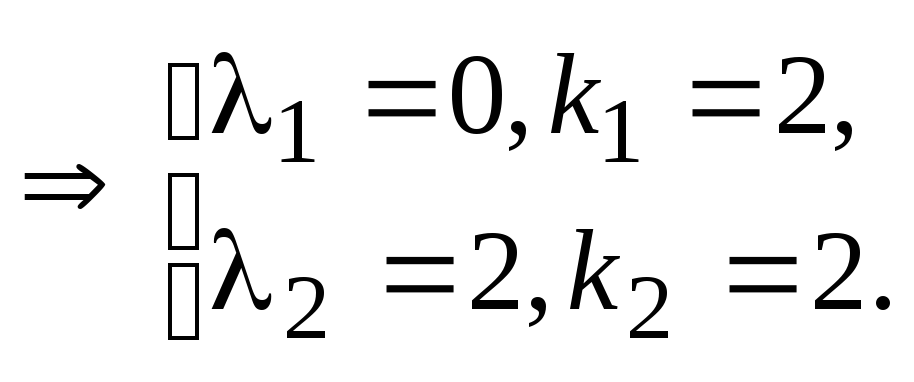
Тепер знайдемо геометричну кратність власних значень, тобто кількість відповідних їм власних векторів.
При
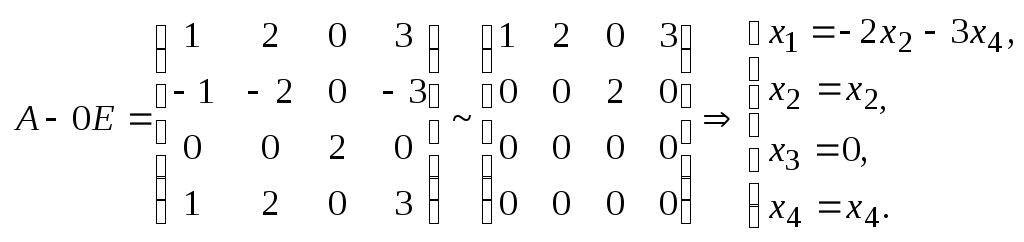
Хай|нехай|, – лінійно незалежні власні вектори, відповідні власному значенню . Значить, геометрична кратність цього кореня рівна двом і збігається з|із| його кратністю алгебри.
При
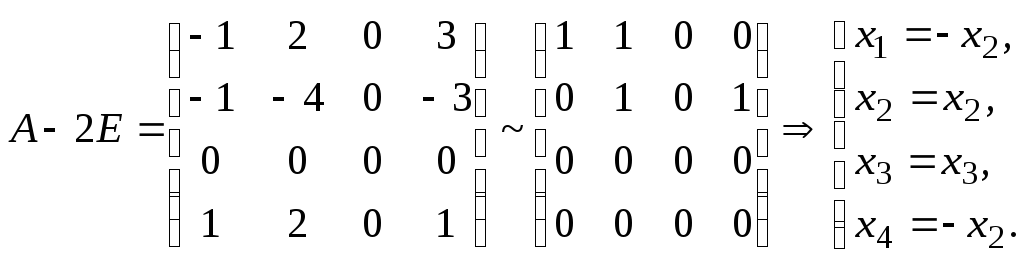
Хай|нехай|, – лінійно незалежні власні вектори, відповідні власному значенню . Значить, геометрична кратність цього кореня рівна двом і також збігається з|із| його кратністю алгебри.
Як видно|показний| з|із| приведеного рішення|розв'язання|, геометрична кратність всіх власних значень збігається з|із| їх кратністю алгебри. Тому матрицю оператора можна привести до діагонального вигляду|виду|. У базисі, складеному власних векторів матриця оператора набере вигляду:
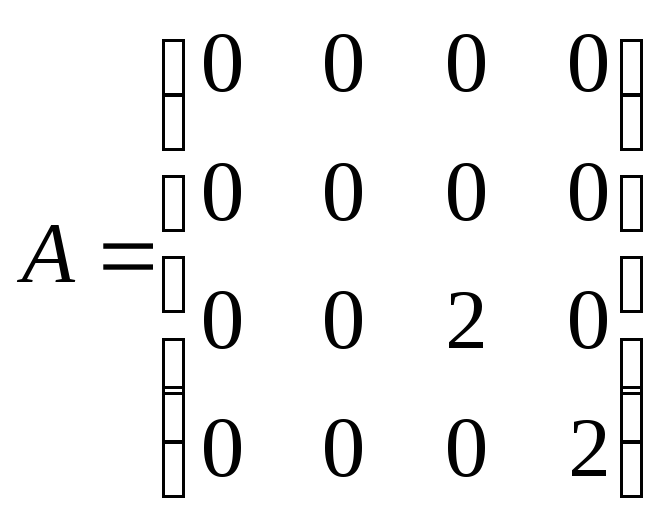 .
.
Лінійний оператор арифметичного простору|простір-час|в стандартному базисі { } заданий матрицею Знайдітьпростори|простір-час|, інваріантні відносно .
Рішення|розв'язання|:
Знайдемо власні значення:
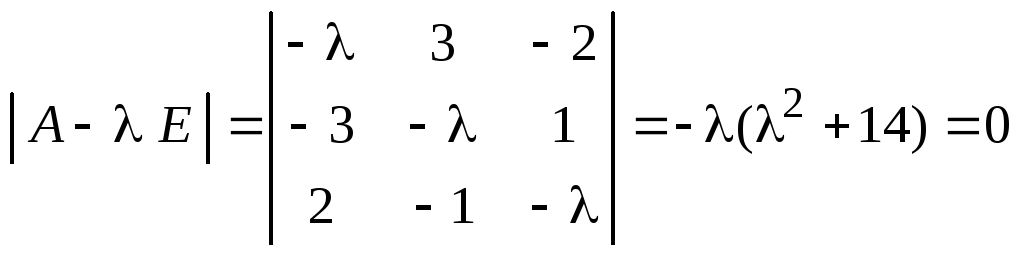 .
.
Над полем дійсних чисел існує єдине власне значення . Знайдемо власні вектори, відповідні знайденому власному значенню:

Хай|нехай|– власний вектор, тоді – інваріантнийпідпростір|простір-час|, відповідний дійсному власному значенню .
h
