4.2. Момент інерції

Інертність тіла при обертальному русі залежить не тільки від маси, а й від її розподілу відносно осі обертання. Інертність тіла при обертанні характеризують моментом інерції відносно осі обертання.

Момент інерції матеріальної точки відносно осі обертання є скалярна фізична величина, яка дорівнює добутку маси на квадрат відстані її від осі:

(4.3)

Момент інерції твердого тіла відносно осі обертання є сума моментів інерції матеріальних точок, з яких складається тіло:

(4.4)

Звичайно момент інерції суцільного тіла визначають інтегруванням:

(4.5)

Як приклад, визначимо момент інерції тонкого однорідного стрижня довжиною і масою відносно осі , яка проходить через його середину (рис. 4.2). Виберемо маленьку ділянку стрижня довжиною і масою яка знаходиться на відстані від осі 00¹. Цю

ділянку можна розглядати як матеріальну точку, тоді для її моменту інерції отримаємо:

(4.6)

Маса елементарної ділянки дорівнює добутку лінійної густини на довжину ділянки: Тоді

(4.7)

Для знаходження моменту інерції стрижня проінтегруємо (4.7)

у межах від до:

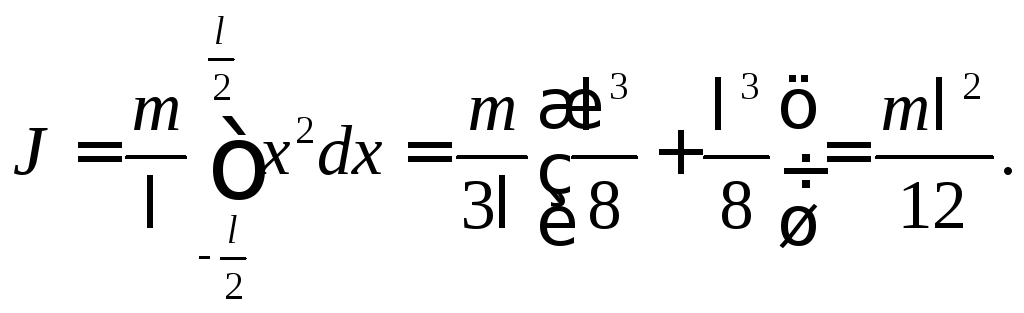(4.8)

Рис.4.2

Моменти інерції геометричних тіл масою

1) суцільний однорідний циліндр чи диск:

(4.9)

2) однорідна куля:

(4.10)

3) прямокутний паралелепіпед (відносно осі, що проходить через

його центр):

(4.11)

При визначенні моменту інерції тіла, що не проходить через центр мас, можна користуватися теоремою Штейнера. Згідно з теоремою, момент інерції тіла відносно осі, що не проходить через центр мас тіла дорівнює моменту інерції тіла відносно осі, що проходить через його центр плюс добуток маси на квадрат відстані між паралельними осями:

(4.12)

Одиниця моменту інерції –

4.3. Момент імпульсу

Моментом імпульсу матеріальної точки відносно осі обертання називається фізична величина, яка дорівнює векторному добутку радіус-вектора на імпульс:

(4.13)

Розкриваючи формулу (3.19), можна записати модуль моменту імпульсу матеріальної точки:

(4.14)

де відстань до осі обертання; кутова швидкість.

Момент імпульсу тіла відносно осі обертання дорівнює сумі моментів імпульсів матеріальних точок, з яких складається тіло:

(4.15)

де момент інерції тіла відносно осі обертання.

У векторній формі момент імпульсу:

Таким чином, момент імпульсу дорівнює добутку моменту інерції тіла на кутову швидкість.

4.4. Робота та кінетична енергія при обертальному русі

Робота зовнішньої сили при обертанні тіла на досить малий кут:

(4.16)

де переміщення точки ; радіус обертання

точки (плече сили); момент зовнішніх сил.

Якщо положення радіус-вектора змінилося від до то роботу знаходять інтегруванням формули (4.16):

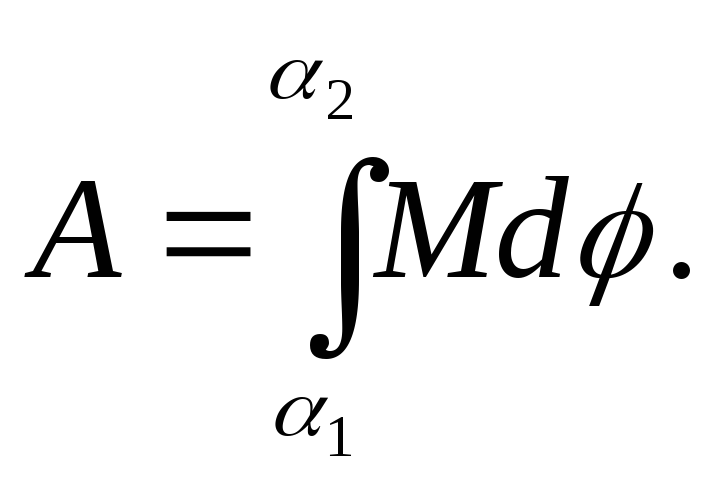(4.17)

Кінетична енергія при обертанні тіла складається з кінетичної енергії окремих його точок:

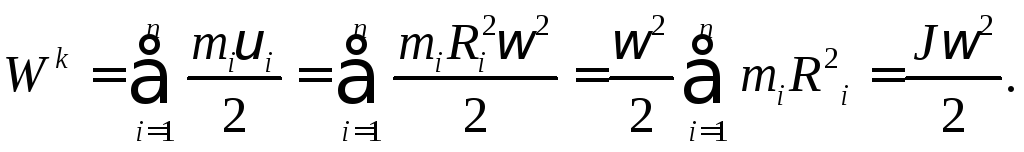(4.18)

Продиференціювавши формулу (4.18), одержимо елементарну

зміну кінетичної енергії обертання:

_.(4.19)

Якщо тіло одночасно перебуває в прямолінійному і обертальному русі, то кінетична енергія визначається сумою енергій поступального і обертального рухів:

(4.20)