
Дискретная Математика / Lektsia_11
.docxЛекция №11
Тема: Канонические формы переключательных функций. Нормальные дизъюнктивные формы переключательных функций.
Содержание
-
Понятие проблемы разрешимости.
-
Нормальные и совершенные нормальные дизъюнктивные формы переключательных функций.
-
Свойства совершенной нормальной дизъюнктивной формы.
Понятие проблемы разрешимости
Определение. Формула называется тождественно истинной, если она при всех значениях, входящих в неё переменных, принимает значение «1».
Примеры:

Определение. Формула называется тождественно ложной, если при всех значениях входящих в неё переменных принимает значение «0»
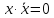
Определение. Формула называется выполнимой (нейтральной), если она не является тождественным 0 или 1 (0v1), т.е. она принимает значение «1» при некоторых значениях входящих в неё переменных.
Для каждой формулы можно выяснить, является ли она выполнимой (равна ли она тождественному 0 или 1). Поставленная задача носит название проблемы разрешимости.
Пусть
 –
формула, определяющая некоторую функцию
от n
переменных:
–
формула, определяющая некоторую функцию
от n
переменных: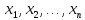 .
Как переменные
.
Как переменные
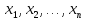 ,
так и функция F
могут принимать лишь два значения, число
же возможных комбинаций значений
переменных
,
так и функция F
могут принимать лишь два значения, число
же возможных комбинаций значений
переменных
 конечно и равно 2n.
Для каждой такой комбинаций можно
определить значение формулы F,
тем самым, определяется выполнима ли
функция или нет.
конечно и равно 2n.
Для каждой такой комбинаций можно
определить значение формулы F,
тем самым, определяется выполнима ли
функция или нет.
Изложенный способ при большом количестве переменных практически неосуществим из-за огромного числа возможных наборов значений переменных
Существует другой способ, основанный на приведении формул к так называемой «нормальной форме».
Синтез комбинационной схемы по существу сводится к определению булевого выражения для заданной ПФ. Дальнейший переход от булевого выражения к системе является однозначным. Вводятся выражения определенного типа, называемые каноническими формами, а затем формируются достаточно простые правила записи любой функции в этих формах. В качестве канонических форм обычно используются СДНФ и СКНФ.
Нормальные и совершенные нормальные дизъюнктивные функции
Выражение
вида
 и называется элементарной конъюнкцией.
и называется элементарной конъюнкцией.
Определение. Логическое произведение любого количества различных независимых переменных (букв), входящих с отрицанием или без него, называется элементарной конъюнкцией.

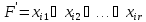 – элементарная
конъюнкция, r
– ранг элементарной конъюнкции и
– элементарная
конъюнкция, r
– ранг элементарной конъюнкции и
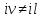 при
при
 .
.
Если функция задана формулой в виде дизъюнкции элементарных конъюнкций, то это дизъюнктивная нармальная форма (ДНФ):
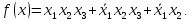
Конституентой
единицы (минтермом) называют переключательную
функцию n
аргументов, которая принимает значение,
равное 1 только на одном кортеже
аргументов. Число различных конституент
единицы среди функций п аргументов
равно числу различных кортежей - наборов,
т.е. равно 2n.
Согласно таблицы, конституентами единицы
являются
 .
.
Утверждение. Любая таблично заданная функция алгебры может быть представлена в виде:
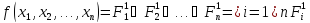
где
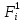 – элементарная конъюнкция ранга n;
– элементарная конъюнкция ранга n;
i
– номера наборов, на которых функция
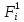 равна 1;
равна 1;
 – символ обобщённой дизъюнкции.
– символ обобщённой дизъюнкции.
Определение. Совершенной дизъюнктивной нормальной формой (СДНФ) переключательной функции называется дизъюнкция тех конституент единицы, которые обращаются в единицу на тех же наборах, что и данная функция.
Любая ПФ имеет одну СДНФ (а количество ее членов равно количеству единичных значений функции) и несколько ДНФ. Любая ДНФ получается в результате большего или меньшего сокращения СДНФ и от любой ДНФ можно перейти к СДНФ. Такой переход называется развертыванием.
Например,
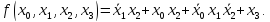

Свойства совершенной нормальной формы (СДНФ)
Определение.
Совершенная ДНФ формула
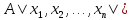 ,
содержащая различные переменные,
называется дизъюнктивная нормальная
форма, обладает следующими свойствами:
,
содержащая различные переменные,
называется дизъюнктивная нормальная
форма, обладает следующими свойствами:
-
в ней нет одинаковых слагаемых;
-
ни одно из слагаемых не содержит двух одинаковых множителей;
-
никакое слагаемое не содержит переменную вместе с её отрицанием;
-
в каждом отдельном слагаемом содержится в качестве множителя либо переменная
 либо её отрицание
либо её отрицание
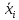 для любого i=1,2,…,n.
для любого i=1,2,…,n.
Краткое основное содержание
-
Любая переключательная функция ПФ отличная от константы «0» имеет одну СДНФ и несколько ДНФ.
-
Любая ДНФ получается в результате сокращения СДНФ.
-
От любой ДНФ можно перейти к СДНФ (это развёртывание).
