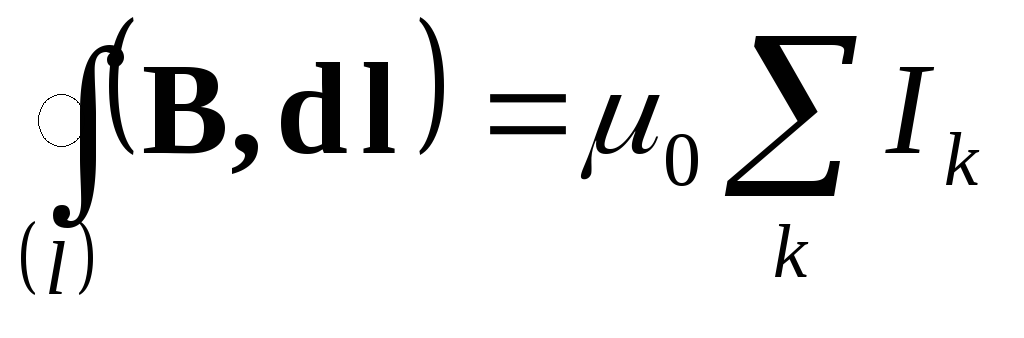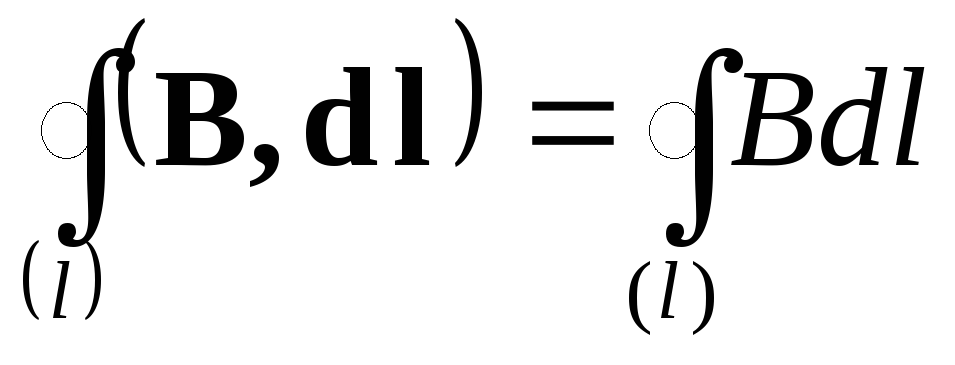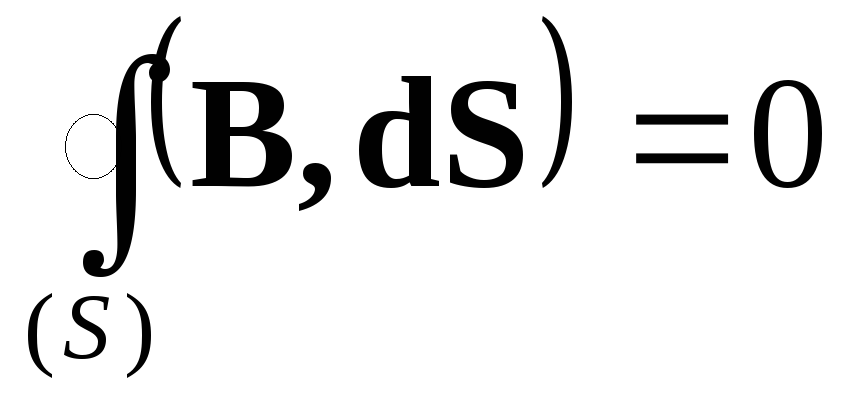• Закон Біо-Савара-Лапласа. Принцип суперпозиції

Залежність вектора індукції магнітного поля, створеного довгим та відносно тонким провідником струму від сили струму та від положення точки спостереження експериментально вивчали французькі фізики Біо та Савар.

Згідно до спостережень Біо та Савара:

• Магнітне поле в точці спостереження прямо пропорційне величині струму 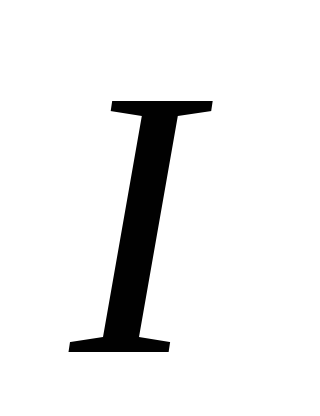в провіднику;

• Магнітне поле зменшується за величиною обернено пропорційно квадрату відстані точки спостереження (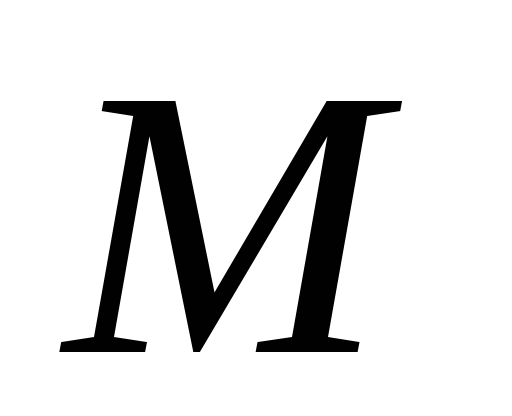) від провідника;

• Кожен елемент струму 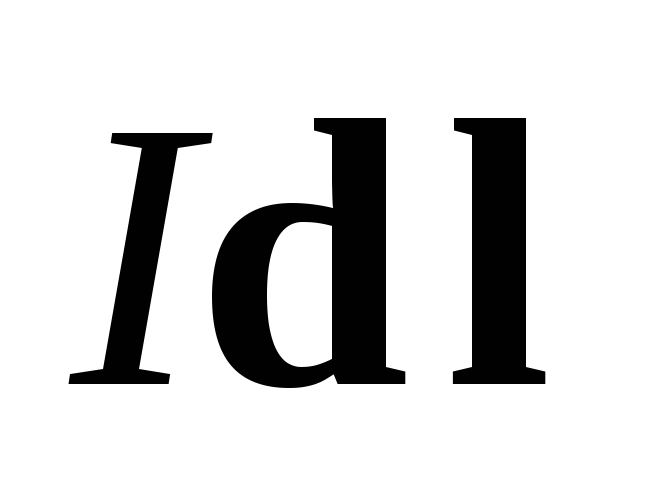створює в точці спостереження 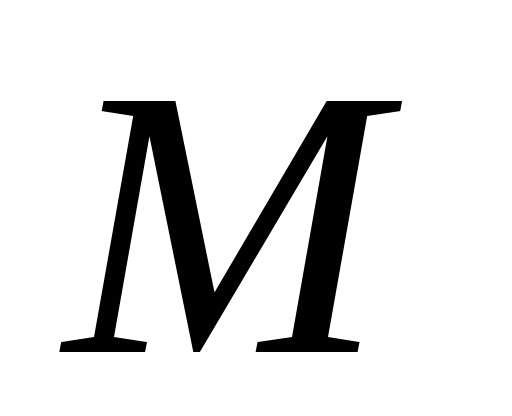мікрополе незалежно від інших елементів струму, причому 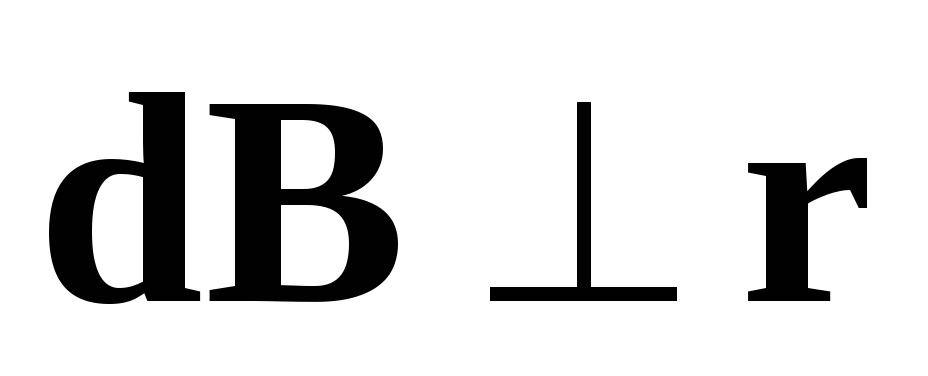і .

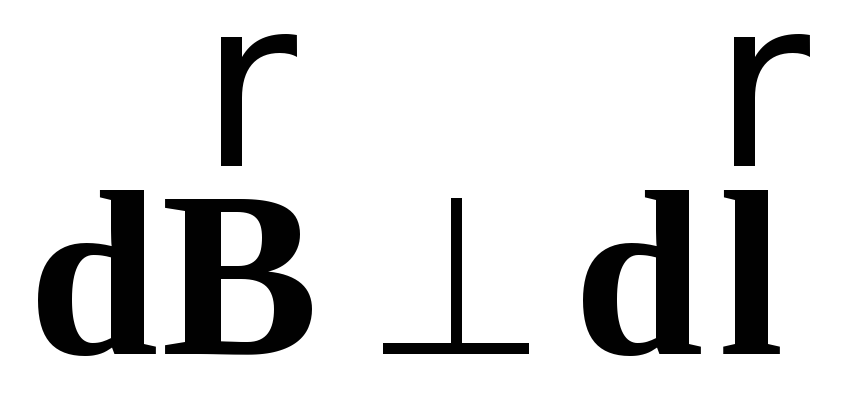Французький математик та фізик Лаплас, аналізуючи результати Біо та Савара, зауважив, що у вакуумі:

(3.6.6)

де Гн/м – так звана магнітна стала, яка забезпечує рівні розмірності обох частин виразу (3.7.6), відомого як закон Біо-Савара-Лапласа.

Лаплас також сформулював принцип суперпозиції магнітних полів, аналогічний принципу суперпозиції для електричного поля. Згідно до цього принципу результуюче поле в точці спостереження є векторною сумою мікрополів, створених кожним елементом провідника зі струмом: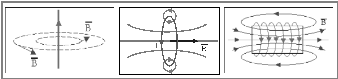

(3.6.7)

Напрям вектора індукції результуючого магнітного поля інколи можна передбачити, виходячи з симетрії розподілу струмів у просторі: тоді магнітне поле зображують у вигляді векторних силових ліній (вектор в кожній точці є як звичайно дотичним до цих ліній). На Мал.3.6.3 зображені магнітні поля для прямого струму, колового струму та довгої котушки (соленоїду). Зверніть увагу – силові лінії магнітного поля завжди є замкненими самі на себе.

• Теорема про циркуляцію вектора індукції магнітного поля та її застосування

Закон Біо-Савара-Лапласа можна в принципі застосувати для розрахунку будь-яких магнітних полів.

Втім значно зручніше користуватися для цього іншим виразом, який можна отримати з закону (3.6.6), і який отримав назву теорема про циркуляцію вектора індукції магнітного поля:

(3.6.8)

Отже циркуляція вектора індукції по довільній замкненій лінії пропорційна алгебраїчній сумі струмів, які охоплюються цією лінією.

Струми різного напряму відносно площини, яка натягнута на лінію циркуляції враховуються з різними знаками, струми, які не охоплюються лінією циркуляції взагалі не враховуються. Нарешті струми враховуються стільки разів (як наприклад для котушки) скільки разів вони перетинають площину, натягнуту на контур циркуляції.

Користуватися (3.6.8) зручно тому, що завжди можна підібрати контур циркуляції так, аби зручно було інтегрувати. Зокрема, можна забезпечити щоб уздовж контуру циркуляції поміж векторами та зберігався кут , тобто вони були одного напрямку, тоді . Наведена умова забезпечується автоматично, якщо в якості лінії циркуляції брати будь-яку силову лінію магнітного поля. В такому разі:

(3.6.9)

Застосуємо (3.6.9) та (3.6.8) до випадку безкінечного прямого струму силою . Силові лінії в такому випадку є концентричні кола. Модуль вектору індукції незмінний уздовж силової лінії: в цьому випадку, отже його можна винести поза межі інтегралу в правій частині (3.6.9). Тоді

(3.6.10)

де - відстань до провідника. Отже:

(3.6.11)

Результат (3.6.11) можна отримати також прямо з закону Біо-Савара-Лапласа, проте значно складнішим способом.

Замкненість силових ліній самих на себе, ненульові значення циркуляції вектора індукції магнітного поля однозначно свідчать про вихровий характер магнітного поля.

Як відомо, для вихрових силових полів виконується також умови:

	(3.6.12)
	(3.6.13)

які є диференціальним та інтегральним математичним формулюванням того фізичного факту, що магнітне поле не має джерел та стоків і тому його потік крізь довільну замкнену поверхню є нульовим. Отже, магнітних зарядів в природі не існує, саме тому силові лінії магнітних полів завжди є самозамкненими.