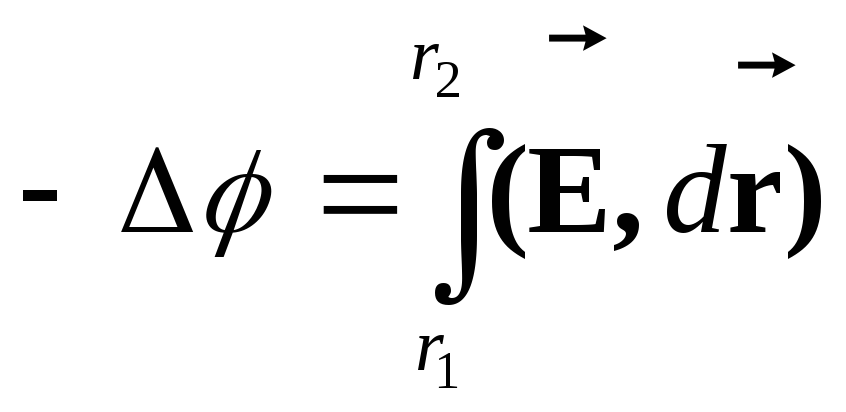• Зв’язок потенціалу з напруженістю електричного поля*

Раніше ми встановили, що електричне поле можна описати чи за допомогою векторної величини (напруженості електричного поля), чи за допомогою скалярної величини (потенціалу електричного поля). Поміж цими величинами повинен існувати зв’язок:

(3.2.27)

Чи у наступному вигляді:

(3.2.28)

Для випадку малих маємо право на в лівій частині перед поставити знак диференціалу, а в правій опустити знак інтегралу; додатково перенесемо знак мінус в праву частину рівності:

(3.2.29)

У випадку скалярного добутку двох векторів маємо право представити напруженість електричного поля у наступному вигляді:

(3.2.30)

Радіус-вектор , як і будь-який вектор можна розкласти на компоненти, тобто: =++ ,де , , - орти (одиничні вектори) відповідних осей, , , - проекції вектора на відповідні координатні осі.

З курсу вищої математики відомо, що похідну, подібну до (3.2.30) можна представити сумою часткових похідних, помножених на відповідний орт:

(3.2.31)

Вираз називають градієнтом потенціалу і позначають або . Отже, в загальному випадку градієнтом є оператор, який діє на скалярні функції типу потенціалу (температури, потенціальної енергії і т.п.)

(3.2.32)

Чи з урахуванням позначення градієнта:

(3.2.31а)

Отже, результатом дії оператору градієнта буде вектор, який спрямований в бік зростання скалярної функції (тобто він вказує напрям зростання скалярної функції), в нашому випадку – потенціалу, а знак „мінус” таким чином вказує на те, що напрями векторів напруженості і градієнта потенціалу протилежні.

Вирази (3.2.31) і (3.2.31а) є так званою диференціальною формою зв’язку між напруженістю та потенціалом електричного поля.

Силові лінії електростатичного поля завжди нормальні до еквіпотенційних поверхонь (тобто перпендикулярні до дотичної площини в кожній точці такої поверхні), що показано на (мал.3.2.10). Отже, маючи картину силових ліній поля можна побудувати еквіпотенційні поверхні, і навпаки. Еквіпотенційні поверхні окремого одиничного точкового позитивного або негативного зряду у відсутності інших зарядів будуть мати вигляд концентричних кіл. Але еквіпотенційні поверхні системи хоча б двох зарядів будуть мати складніший характер.

Рекомендована література:

1. Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1982.–448 С.

2. Дягилев Ф.М. Из истории физики и жизни ее творцов. – М.: Просвещение, 1986.–255 С.

3. Хромов Ю.А. Физики: биографический справочник. – К.: Наукова думка, 1977.–511 С.

4. Хрестоматия по физике: учеб пособие по физике для уч-ся 8-10 классов. – М.: Просвещение, 1982.–223 С.

5. Савельев И.В. Курс общей физики. Том II. Электричечтво – М.: Наука, 1988 – с.11-34.

6. Кучерук І.М., Горбачук І.Т. Загальна фізика: Електрика і магнетизм. – К.: Вища шк., 1995. – с.3-26.

7. Бушок Г.Ф., Левандовський В.В., Півень Г.Ф. Курс фізики. Кн. 1. Фізичні основи механіки. Електрика і магнетизм. – К.: Либідь, 2001. – с.220-230.

8. Детлаф А.А., Яворский Б.М. Курс физики: – М.: Высш.шк.., 1989. – с.154-162.

9. Калашников С.Г. Электричество. – М.:Наука, 1985. – 576 С.

Факультет машинобудування
Лектор Дон Н.Л.		стор. 13 з 13