Херсонський державний технічний університет Кафедра загальної та прикладної фізики

ЕЛЕКТРИКА І МАГНЕТИЗМ Лекція 3.2. Електростатика (продовження)

	3.2. ЕЛЕКТРОСТАТИКА (продовження)
	Теорема Остроградського-Гаусса в інтегральній формі
	Теорема Остроградського-Гаусса в диференціальній формі
	Застосування теореми Остроградського-Гаусса*
	Робота сил електричного поля. Потенціал
Зв’язок потенціалу з напруженістю електричного поля

• Теорема Остроградського-Гаусса в диференціальній формі

На основі закону Кулона (3.1.7) і принципу суперпозиції (3.1.9) можна визначити напруженість практично будь-якої системи нерухомих зарядів. Однак такий спосіб розв’язання задач електростатики часто призводить до надто громіздких обчислень. Задача істотно спрощується, якщо скористатися деякими теоремами про загальні властивості електростатичного поля. Однією з таких теорем є теорема Остроградського-Гаусса. Ця теорема має також принципове значення. Математичний запис основного закону електростатики у формі (3.1.7) відповідає теорії далекодії. Теорема Остроградського-Гаусса дає можливість звести основні рівняння електростатики до диференціальної форми і узгодити їх, таким чином з теорією близькодії.

Т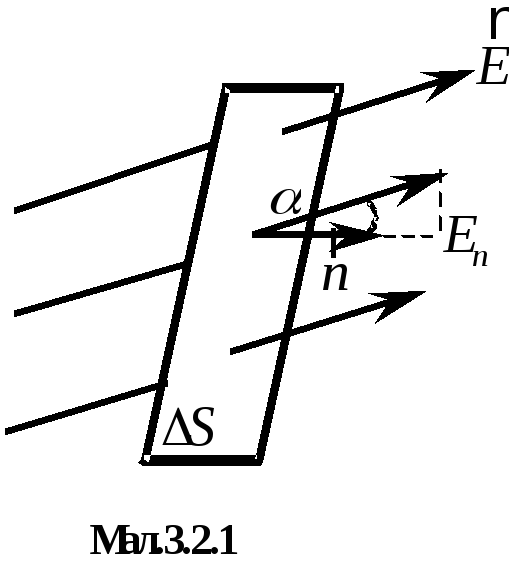 еорема Остроградського-Гаусса пов’язує потік вектора напруженості електростатичного поля через довільну замкнену поверхню з зарядом, який охоплюється цією поверхнею.

Нехай дано однорідне поле напруженістю . Розмістимо в цьому полі плоску поверхню , нормаль до якої утворює кут з вектором (Мал.3.2.1). Величину

(3.2.1)

Н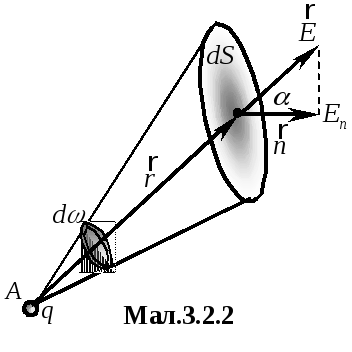азивають потоком вектора через поверхню ( – проекція на нормаль ). Потік може бути додатним або від’ємним залежно від знака проекції , який визначається знаком . Вибір додатного напряму умовний (додатною вважають зовнішню нормаль до поверхні ).

Якщо поле неоднорідне і поверхня не плоска, то уявно її розбивають на елементи , які можна наближено вважати плоскими, а поле в її межах – однорідним (мал. 3.2.2). Тоді елементарний потік вектора

(3.2.2)

А повний потік через поверхню

(3.2.2а)

Для доведення теореми Остроградського-Гаусса обчислимо спочатку потік вектора напруженості електростатичного поля, створюваного точковим зарядом, через довільну замкнену поверхню.

Нехай точковий заряд розміщений у точці А (мал.3.2.2), а елемент поверхні міститься на відстані . Тоді

Скориставшись формулою (3.2.1), отримуємо

(3.2.3)

Де – проекція на поверхню сфери радіуса . Крім того, – тілесний кут, під яким з точки А видно елемент поверхні. Тоді (3.2.3) можна переписати:

(3.2.3а)

Вважатимемо додатним, якщо кут між напрямами і гострий, і від’ємним, якщо кут тупий.

Обчислимо повний потік вектора через довільну замкнену поверхню. Розглянемо два випадки.

• Точковий заряд міститься всередині замкненої поверхні

Довільний конус з вершиною в точці розміщення заряду і тілесним кутом виокремить на заданій поверхні одну елементарну поверхню . Незалежно від форми поверхні елементарний потік вектора визначатиметься лише потоком через елементарну площу , оскільки при наявності інших перерізів потоки через них будуть однакові за величиною, протилежні за знаком і їхня сума дорівнюватиме нулю. Отже, в цьому випадку

А повний потік через довільну замкнену поверхню , яка охоплює даний точковий заряд

(3.2.4)

Оскільки стерадіанів.

Якщо поверхня охоплює систему точкових зарядів, то

(3.2.4а)

• Точковий заряд міститься зовні від замкненої поверхні

У цьому разі довільний конус з вершиною в місці розташування точкового заряду і тілесним кутом виокремить завжди парну кількість елементарних поверхонь на замкненій поверхні . Елементарні потоки через кожну з цих поверхонь будуть однакові за величиною, але протилежні за знаками. Тому їхній сумарний елементарний потік дорівнює нулю, а отже, і повний потік

(3.2.4б)

Обидва випадки (заряди всередині замкненої поверхні і заряди поза поверхнею) описуються формулою (3.2.4а), яка є математичним виразом теореми Остроградського-Гаусса:

Потік вектора напруженості електростатичного поля у вакуумі через довільну замкнену поверхню зсередини назовні дорівнює алгебраїчній сумі тих зарядів , які охоплюються поверхнею , поділеній на електричну сталу .

У випадку об’ємних і поверхневих зарядів

(3.2.5)

Позитивному заряду відповідає додатний потік напруженості, негативному – від’ємний. Отже, заряди є своєрідними джерелами і стоками потоку напруженості поля (позитивні заряди – джерелами, негативні – стоками поля) (мал.3.2.3).

• Теорема Остроградського-Гаусса в диференціальній формі

Величини, що входять у вираз теореми Остроградського-Гаусса, характеризують різні точки електричного поля. Так, якщо вектор характеризує точки деякої замкненої поверхні, то електричний заряд стосується точок об’єму, обмеженого цією поверхнею. Таку форму запису теореми називають інтегральною. Отримаємо аналітичний вираз цієї теореми в диференціальній формі, тобто знайдемо співвідношення між фізичними величинами, які характеризують ту саму точку поля. Для цього знайдемо потік вектора напруженості електричного поля через поверхню нескінченно малого прямокутного паралелепіпеда з ребрами , який охоплює заряд, розподілений з об’ємною густиною (мал.3.2.4). Нехай у вершині А з координатами () проекції вектора напруженості . Потік через грань , яка проходить через точку А, буде . Знак “-“ вказує на те, що напрям нормалі до цієї грані і додатний напрям протилежні. Потік через паралельну грань, яка зміщена вздовж осі на

Результуючий потік через зазначені паралельні грані матиме вигляд:

Аналогічно потоки через дві інші пари паралельних граней:

Повний потік вектора через всю поверхню паралелепіпеда

Заряд, який охоплюється паралелепіпедом зі сторонами при рівномірному його розподілі з об’ємною густиною , дорівнює . Тоді за теоремою Остроградського-Гаусса (3.2.4а)

(3.2.6)

Співвідношення (3.2.6) виражає теорему Остроградського-Гаусса у диференціальній формі. Оскільки розміри паралелепіпеда нескінченно малі, то можна прийняти, що значення вектора на поверхні цього паралелепіпеда і заряд, який охоплюється поверхнею, по суті стосуються тієї самої точки.

За теоремою Остроградського-Гаусса у формі (3.2.5) для об’ємних зарядів з урахуванням того, що , можна записати

(3.2.7)

Де – довільна замкнена поверхня, – обмежений нею об’єм.

У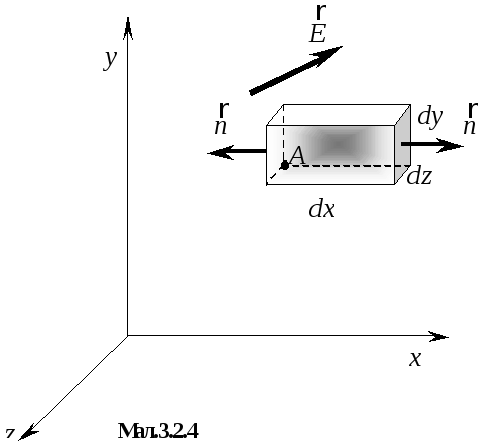 векторному аналізі доведено, що границя відношення потоку будь-якого вектора , визначеного в усіх точках векторного поля, через замкнену поверхню до величини об’єму , обмеженого цією поверхнею, при не залежить від форми . Границю цього відношення називають розходженням, чи дивергенцією, вектора в точці, в яку стягується об’єм , і позначають символом . За означенням

За теоремою Гаусса . Для вектора напруженості електричного поля маємо:

(3.2.8)

Чи з урахуванням (3.2.7)

(3.2.9)

Оскільки – довільний об’єм, то очевидна рівність

(3.2.10)

Порівнюючи з (3.2.6) маємо:

(3.2.11)

Формула (3.2.11) дає можливість обчислити дивергенцію в декартових координатах. Дивергенція фізично характеризує потужність джерел чи стоків.