Похідна за напрямом

Похідна від функції за напрямом характеризує швидкість зміни функції за цим напрямом і обчислюється за формулою:

.

Приклад 7. Знайти похідну функції у точціза напрямом вектора.

Розв’язання.

; ;

; .

Враховуючи , маємо

; ;

.

Градієнт функції

Градієнтом функції називається вектор, який показує напрямок найбільшого зростання функції і проекціями якого на координатні осі,,є відповідно,,:

.

Приклад 8. Знайти градієнт функції у точці.

Розв’язання.

; ;;;

.

Метод найменших квадратів

Нехай – послідовність значень незалежної змінної, а– послідовність відповідних значень залежної змінної.Припустимо, що точки ,, ...,приблизно розташовуються на одній прямій. Поставимо за мету підібрати рівняння прямої , яка є найточнішим наближенням залежності міжта.

Зміст методу найменших квадратів полягає у тому, що шукану лінію підбирають таким чином, щоб сума квадратів відхилень була б найменшою. Маємо

.

Використовуючи необхідну умову екстремуму (9.5) функції , отримаємо:

.

Тобто коефіцієнти іпрямоїобчислюються із системи рівнянь:

(9.7)

Приклад 9. Експериментально одержані значення функціїу п’яти точках, які записані у таблиці:

	1	2	3	4	5
	3,9	4,1	3,5	2,5	2,4

Методом найменших квадратів знайти функцію , що виражає приблизно функцію. Зробити рисунок, на якому побудувати графік функціїта експериментальні точки.

Розв’язання. Для знаходження коефіцієнтів іза формулами (9.7) обчислимота, результати занесемо у таблицю:

	1	1	3,9	3,9
	2	4	4,1	8,2
	3	9	3,5	10,5
	4	16	2,5	10
	5	25	2,4	12
	15	55	16,4	44,6

Маємо:

.

Отже,

.

Пряма та експериментальні точки показані на рис. 9.14.

Рис. 9.14

Варіанти для самостійного розв’язання

Варіант 1

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,3	5,3	3,8	1,8	2,3

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 2

1. Знайти та відобразити на рисунку область визначення функції .

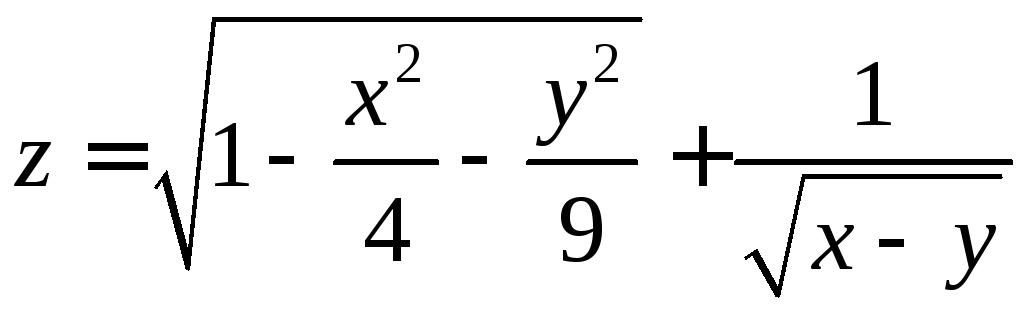2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,5	5,5	4,0	2,0	2,5

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 3

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,7	5,7	4,2	2,2	2,7

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 4

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,9	5,9	4,4	2,4	2,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 5

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,1	6,1	4,6	2,6	3,1

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 6

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,9	4,9	3,4	1,4	1,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 7

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,2	6,2	4,7	2,7	3,2

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 8

1. Знайти область існування функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:,,.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,5	6,5	5,0	3,0	3,5

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 9

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,7	6,7	5,2	3,2	3,7

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 10

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в точціу напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,9	6,9	5,4	3,4	3,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 11

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідну функції.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,3	6,3	4,8	2,8	3,3

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 12

1. Знайти та відобразити на рисунку область існування функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в області:;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,3	4,3	2,8	0,8	1,4

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 13

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	6,3	7,2	5,9	3,8	4,2

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 14

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	2,9	3,8	2,4	0,5	0,8

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 15

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	1,8	1,4	3,3	4,8	3,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 16

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,1	2,4	4,2	5,5	4,4

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 17

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	2,3	2,0	4,2	5,8	5,2

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 18

1. Знайти та відобразити на рисунку область визначення функції .

2. Знайти похідні другого порядку від функції .

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в замкненій області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,5	5,7	4,4	2,6	1,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 19

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція задовольняє рівнянню Лапласа.

3. Скласти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в області:;;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	4,7	5,9	4,6	1,8	2,2

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 20

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція задовольняє рівнянню Лапласа.

3. Скласти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти найменше та найбільше значення функції в області:;.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	5,1	5,9	4,2	2,0	2,3

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 21

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція , де, а, задовольняє рівняння Гельмгольца.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Виготовити з картону прямокутну коробку (без кришки) ємності з найменшими витратами матеріалу.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Знайти похідну функції в точціу напрямі градієнта цієї функції.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,2	2,4	4,6	5,9	4,8

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 22

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція , де, а– довільні сталі, задовольняє рівняння Максвелла.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. В кулю діаметру вписати прямокутний паралелепіпед найбільшого об’єму.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Знайти похідну функції в точціу напрямі градієнта цієї функції.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,7	3,2	5,2	6,7	5,8

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 23

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція задовольняє рівняння.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти розміри циліндричної посудини найбільшої місткості з поверхнею .

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Знайти градієнт функції в точціта похідну в цій точці у напрямі градієнта.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	3,5	3,0	5,0	6,5	5,6

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 24

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція задовольняє рівнянню.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Поверхня прямокутного паралелепіпеда дорівнює . Знайдіть розмір паралелепіпеда найбільшого об’єму.

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Знайти градієнт функції в точціта похідну в цій точці у напрямі вектора.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	2,9	2,4	4,5	5,8	4,9

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.

Варіант 25

1. Знайти та відобразити на рисунку область визначення функції .

2. Показати, що функція задовольняє рівняння.

3. Знайти рівняння дотичної площини і нормалі до поверхні в точці.

4. Знайти прямокутний паралелепіпед найбільшого об’єму за умови, що довжина його діагоналі дорівнює .

5. Замінюючи приріст відповідної функції диференціалом, наближено обчислити .

6. Для функції знайти градієнт в точціта похідну в цій точці у напрямі градієнта.

7. Експериментально одержано значення функції :

	1	2	3	4	5
	1,9	2,4	4,4	5,7	4,6

Методом найменших квадратів знайти функцію , яка виражає наближено (апроксимує) функцію. Зробити рисунок, на якому в декартовій прямокутній системі координат побудувати експериментальні точки та графік апроксимуючої функції.