
3.8. Процесс ортогонализации Грама - Шмидта
В каждом ли евклидовом пространстве нужно уметь находить и строить ортонормированный базис. Построить ортонормированный базис можно, отталкиваясь от некоторого исходного базиса, при помощи алгоритма, который называют процессом ортогонализации Грама — Шмидта. Изложим этот алгоритм.
Пусть
 —
некоторый базис вп-мерном
евклидовом
пространстве
—
некоторый базис вп-мерном
евклидовом
пространстве
 .
Модифицируя
этот базис, мы будем строить новый базис
.
Модифицируя
этот базис, мы будем строить новый базис
 ,
который
будет ортонормированным. Последовательно
вычисляем векторы
,
который
будет ортонормированным. Последовательно
вычисляем векторы
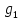 и
и
 ,
,
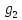 и
и
 и
т.д. по формулам:
и
т.д. по формулам:
 (3.9)
(3.9)
Геометрическая
иллюстрация этой последовательности
вычислений при п
=
3 (линейное пространство
 )
приведена на рис. 3.4.
)
приведена на рис. 3.4.

Рис. 3.4
Для
обоснования алгоритма нужно показать,
что ни один из последовательно вычисляемых
векторов
 не
является нулевым
вектором (иначе
процесс оборвался бы преждевременно)
и что все векторы
не
является нулевым
вектором (иначе
процесс оборвался бы преждевременно)
и что все векторы
 ,
попарноортогональны.
Тогда
и векторы
,
попарноортогональны.
Тогда
и векторы
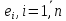 ,
образуют ортогональную систему, но при
этомнорма
каждого
из этих векторов равна единице.
Ортогональная система
из
п
ненулевых
векторов,
согласно
теореме 3.4, линейно
независима и
поэтому в п-мерном
евклидовом пространстве является
базисом.
,
образуют ортогональную систему, но при
этомнорма
каждого
из этих векторов равна единице.
Ортогональная система
из
п
ненулевых
векторов,
согласно
теореме 3.4, линейно
независима и
поэтому в п-мерном
евклидовом пространстве является
базисом.
Доказательство
опирается на метод математической
индукции. В соответствии с этим методом
мы будем доказывать, что для любого
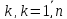 ,
векторы
,
векторы
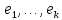 образуют
ортогональную систему и длины их равны
единице. Это утверждение очевидно при
образуют
ортогональную систему и длины их равны
единице. Это утверждение очевидно при
 ,
так как в этом случае вектор
,
так как в этом случае вектор ненулевой,
потому что равен вектору
ненулевой,
потому что равен вектору
 единичной
длины, а систему векторов, состоящую из
одного вектора, считают ортогональной
по определению.
единичной
длины, а систему векторов, состоящую из
одного вектора, считают ортогональной
по определению.
Пусть
векторы
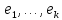 ,
образуют ортогональную систему. Вычислим
новый вектор
,
образуют ортогональную систему. Вычислим
новый вектор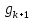 по
формуле
по
формуле
 (3.10)
(3.10)
Предположив,
что
 ,
заключаем,
что
,
заключаем,
что
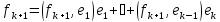
т.е.
вектор
 является
линейной комбинацией векторов
является
линейной комбинацией векторов
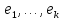 ,
которые в силу(3.9)
выражаются
через векторы
,
которые в силу(3.9)
выражаются
через векторы
 .
Следовательно,
этот вектор является линейной
комбинацией системы
векторов
.
Следовательно,
этот вектор является линейной
комбинацией системы
векторов
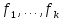 ,
а
система векторов
,
а
система векторов
 согласно
теореме 1.1,
линейно
зависима. Но это противоречит условию
линейной независимости системы
согласно
теореме 1.1,
линейно
зависима. Но это противоречит условию
линейной независимости системы
 .
.
Итак,
предположение о том, что
 ,
привело
к противоречию и потому неверно. Нам
остается убедиться, что вектор
,
привело
к противоречию и потому неверно. Нам
остается убедиться, что вектор
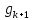 ортогонален
каждому из векторов
ортогонален
каждому из векторов
 .
Умножим равенство(3.10)
скалярно
на вектор
.
Умножим равенство(3.10)
скалярно
на вектор
 ,
где
,
где .
Учитывая, что векторы
.
Учитывая, что векторы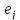 попарно
ортогональны при
попарно
ортогональны при
 ,
получим:
,
получим:


так
как
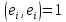 .
Следовательно,
векторы
.
Следовательно,
векторы
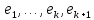 ,
где
,
где образуют
ортогональную систему векторов и имеют
единичную длину.
образуют
ортогональную систему векторов и имеют
единичную длину.
Итак в конечномерном евклидовом пространстве существует ортонормированный базис.
В
процессе ортогонализации любой вектор
 можно заменить на коллинеарный ему
ненулевой вектор
можно заменить на коллинеарный ему
ненулевой вектор Если система
Если система векторов
линейно зависима, то в процессе
ортогонализации будем получать (на
некоторых шагах) нулевые векторы.
векторов
линейно зависима, то в процессе
ортогонализации будем получать (на
некоторых шагах) нулевые векторы.
При
практических применениях процесс Грама
— Шмидта удобно модифицировать так,
чтобы ограничиться вычислением векторов
 и
не использовать их нормированные
варианты
и
не использовать их нормированные
варианты
 .
В
этом случае нужно последовательно
вычислить векторы
.
В
этом случае нужно последовательно
вычислить векторы
 а
затем провести их нормировку, приводящую
к векторам
а
затем провести их нормировку, приводящую
к векторам
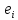 .
Чтобы модифицировать алгоритм вычислений,
в левой колонке (3.9) заменим векторы
.
Чтобы модифицировать алгоритм вычислений,
в левой колонке (3.9) заменим векторы
 на
на
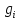 ,согласно
формулам в правой колонке. Получим:
,согласно
формулам в правой колонке. Получим:

Пример
3.14. В
линейном пространстве
 рассмотрим
векторы
рассмотрим
векторы
 и
и
 с
длинами
с
длинами
 ,
,
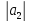 =6
и углом между ними
=6
и углом между ними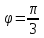 .
.
Так
как векторы ненулевые, а угол между ними
не равен 0 или
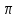 ,
они
не коллинеарны, а потому образуют базис
в
,
они
не коллинеарны, а потому образуют базис
в
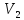 .
Построим при помощи процесса Грама -
Шмидта ортонормированный базис. Согласно
описанному выше алгоритму находим:
.
Построим при помощи процесса Грама -
Шмидта ортонормированный базис. Согласно
описанному выше алгоритму находим:


Затем
полученные векторы
 и
и
 нормируем:
нормируем:





Векторы
 и
и
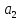 и
построенный по ним ортонормированный
базис
и
построенный по ним ортонормированный
базис
 и
и
 представлены
на рис. 3.5.
представлены
на рис. 3.5.

Пример 3.14. Даны системы векторов евклидовых пространств:
a)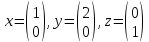 элементы
пространства
элементы
пространства
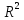 со скалярным произведением
со скалярным произведением
б)


 -
элементы пространства
-
элементы пространства со скалярным произведением
со скалярным произведением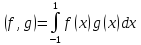
Провести ортогонализацию данных векторов.
а) Заметим, что система векторов х, у , z линейно зависимая, так как х и у пропорциональны, поэтому используем процесс ортогонапизации Грама - Шмидта с учетом замечаний.
Полагаем
 .
Вычисляем
.
Вычисляем

Получили нулевой вектор.
3. Вычисляем


Проверим условие ортогональности

Для
получения ортонормированной системы
исключаем нулевой вектор
 ,
а остальные нормируем:
,
а остальные нормируем:

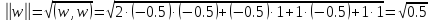
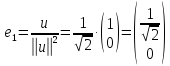
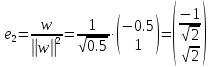
Таким
образом, для системы трех векторов х,
у,
z
построена ортогональная система из
трех векторов и
, v,
w
и ортонормированная система из двух
векторов
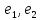 .
Линейные оболочки этих трех систем
совпадают между собой (и со всем
пространством
.
Линейные оболочки этих трех систем
совпадают между собой (и со всем
пространством
 ).
).
б)
Полагаем

Вычисляем

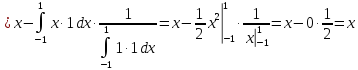

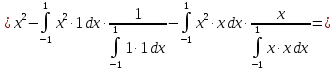
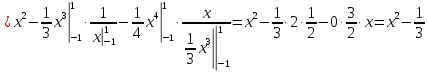
Получили
ортогональные многочлены
 ,
,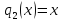 ,
, .
Выполним нормировку:
.
Выполним нормировку:





Получили ортонормированные многочлены
