3.6. Ортогональные и ортонормированные базисы

Евклидово пространство является линейным пространством. Поэтому правомерно говорить о его размерности и его базисах. Как и произвольные линейные пространства, евклидовы пространства можно разделить на бесконечномерные и конечномерные.

Если базис евклидова пространства представляет собой ортогональную систему векторов, то этот базис называют ортогональным. В силу теоремы 3.4 любая ортогональная система ненулевых векторов линейно независима, и если она в п-мерном евклидовом пространстве состоит из п векторов, то является базисом.

В линейном пространстве все базисы равноправны. В евклидовом же пространстве наличие скалярного умножения позволяет выделить среди всех базисов ортогональные и ортонормированные, которые более удобны и играют в линейной алгебре роль, аналогичную роли прямоугольной системы координат в аналитической геометрии.

Определение 3.7. Ортогональный базис называют ортонормированным, если каждый вектор этого базиса имеет норму (длину), равную единице.

Дополнительное требование к нормам векторов в ортонормированном базисе в принципе не является существенным, так как любой ортогональный базис легко преобразовать в ортонормированный, умножая векторы на соответствующие норми­рующие коэффициенты (разделив каждый вектор базиса на его длину). Однако дополнительная нормировка векторов упрощает изложение теории.

Пример 3.11. Система из трех векторов

в евклидовом арифметическом пространстве образует ортогональный базис, потому что . Этот базис не является ортонормированным, так как, например, . Чтобы этот базис сделать ортонормированным, нужно векторыа и b разделить на их нормы, т.е. на число.

Пример 3.12. Векторы i, j образуют ортонормированный базис в пространстве свободных векторов на плоскости. Точно так же векторыi, j, k образуют ортонормированный базис в пространстве .

3.7. Вычисления в ортонормированном базисе

Использование ортонормированных базисов облегчает вычисление скалярного произведения по координатам векторов. Пусть в евклидовом пространстве задан некоторый базис . Рассмотрим два произвольных вектора х и у в этом пространстве. Эти векторы представляются в базисе е своими координатами:

,

Запишем эти разложения векторов по базису в матричной форме:

, ,,,

Скалярное произведение векторов х и у может быть выражено через скалярные произведения векторов базиса:

Составив из скалярных произведений базисных векторов квадратную матрицу порядка n, мы можем записать скалярное произведение заданных векторов в матричной форме:

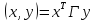
Матрица Г является симметрической в силу коммутативности операции скалярного умножения. Ее называют матрицей Грама системы векторов .

Пусть базис е является ортонормированным. Тогда скалярное произведение при несовпадающих i и j равно нулю, а скалярные квадраты базисных векторов равны 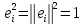. Это значит, что для ортонормированного базиса матрицаГ является единичной. Поэтому

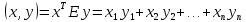
В частности, в ортонормированном базисе норма вектора x, которая выражается через скалярный квадрат этого вектора, может быть вычислена по формуле

(3.7)

а для косинуса угла междуненулевыми векторами x и у получаем выражение

(3.8)

В ортонормированном базисе также упрощается вычисление координат вектора: они выражаются через скалярные произведения. Если , то, умножив равенство скалярно на вектор 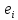, находим, что

,

Пример 3.13. В евклидовом арифметическом пространстве найдем угол между векторами). Согласно формуле (3.8),