
re / Лекция 7
.docx
3.9. Ортогональное дополнение
Как
следует из теоремы 2.7, в произвольном
линейном
пространстве С любое
линейное
подпространство
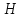 имеет
прямое
дополнение, т.е.
такое линейное подпространство
имеет
прямое
дополнение, т.е.
такое линейное подпространство
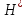 что
что
 Такое линейное подпространство
Такое линейное подпространство
 не
является единственным. Однако в случае
евклидова
пространства, среди
всех возможных прямых дополнений к
данному линейному подпространству одно
выделяется.
не
является единственным. Однако в случае
евклидова
пространства, среди
всех возможных прямых дополнений к
данному линейному подпространству одно
выделяется.
Определение
3.8. Ортогональным
дополнением линейного
подпространства
 в евклидовом пространстве
в евклидовом пространстве
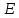 называют множество
называют множество
 -
всех
векторов
-
всех
векторов
 ,
ортогональных
каждому
вектору линейного подпространства
,
ортогональных
каждому
вектору линейного подпространства
 .
.
 Пример
3.15. В
евклидовом пространстве
Пример
3.15. В
евклидовом пространстве
 свободных
векторов рассмотрим
линейное подпространство
свободных
векторов рассмотрим
линейное подпространство
 векторов,
параллельных данной плоскости (см.
пример 2.1). Тогда ортогональным дополнением
векторов,
параллельных данной плоскости (см.
пример 2.1). Тогда ортогональным дополнением
 - будет
множество векторов, перпендикулярных
к этой плоскости (рис. 3.6, а), в то время
как в качестве прямого дополнения
- будет
множество векторов, перпендикулярных
к этой плоскости (рис. 3.6, а), в то время
как в качестве прямого дополнения
 можно взять подпространство векторов,
коллинеарных произвольной прямой,
пересекающей плоскость в единственной
точке, т.е. не параллельной плоскости и
не лежащей в этой плоскости (рис. 3.6, б).
Отметим, что в данном случае
можно взять подпространство векторов,
коллинеарных произвольной прямой,
пересекающей плоскость в единственной
точке, т.е. не параллельной плоскости и
не лежащей в этой плоскости (рис. 3.6, б).
Отметим, что в данном случае
 является
линейным подпространством в
является
линейным подпространством в
 .
.
б линейного
подпространства
линейного
подпространства
 в евклидовом подпространстве
в евклидовом подпространстве
 является линейным подпространством в
является линейным подпространством в
 ,
причем
,
причем
 и
и
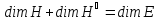 .
.
Чтобы
доказать, что
 -
является
линейным подпространством в
-
является
линейным подпространством в
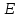 ,
нужно проверить условия 1) и 2) определения
2.1. Взяв два произвольных вектора x
и у,
принадлежащих
,
нужно проверить условия 1) и 2) определения
2.1. Взяв два произвольных вектора x
и у,
принадлежащих
 ,
умножим
скалярно
их
сумму
на
произвольный вектор
,
умножим
скалярно
их
сумму
на
произвольный вектор
 Получим:
Получим:

т.е.
для любых векторов x
и у
из
множества
 их
сумма
их
сумма
 принадлежит
тому же множеству.
принадлежит
тому же множеству.
Теперь
рассмотрим произведение
вектора
 на
произвольное
действительное число
на
произвольное
действительное число
 .
Для произвольного вектора
.
Для произвольного вектора


и
поэтому
 если
если
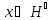 .
Следовательно,
.
Следовательно,
 является
линейным подпространством в
является
линейным подпространством в
 .
.
Отметим,
что любой вектор x,
принадлежащий пересечению
 ,
ортогонален
самому себе:
,
ортогонален
самому себе:
 ,
так как любой вектор из
,
так как любой вектор из
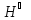 .-
ортогонален
любому вектору подпространства
.-
ортогонален
любому вектору подпространства
 ..
Но
вектор ортогонален самому себе лишь в
том случае, когда он нулевой
(аксиома г)
скалярного
умножения). Поэтому
..
Но
вектор ортогонален самому себе лишь в
том случае, когда он нулевой
(аксиома г)
скалярного
умножения). Поэтому
 ,
а
сумма
,
а
сумма
 -
рассматриваемых
линейных
подпространств является
прямой
(см.
теорему 2.3). Докажем, что эта прямая сумма
совпадает со всем евклидовым пространством
-
рассматриваемых
линейных
подпространств является
прямой
(см.
теорему 2.3). Докажем, что эта прямая сумма
совпадает со всем евклидовым пространством
 .
.
Выберем
некоторый ортонормированный
базис
 в
линейном подпространстве
в
линейном подпространстве
 и дополним его до базиса
и дополним его до базиса
 во
всем евклидовом пространстве
во
всем евклидовом пространстве
 ,
,
 .
Исходя из этого базиса построим при
помощи процесса Грама - Шмидта
ортонормированный базис
.
Исходя из этого базиса построим при
помощи процесса Грама - Шмидта
ортонормированный базис
 в
в
 .
Так как первые т
векторов
.
Так как первые т
векторов
 исходного
базиса попарно ортогональны и имеют
единичную длину, процесс ортогонализации
оставит их без изменения, Т.е.
исходного
базиса попарно ортогональны и имеют
единичную длину, процесс ортогонализации
оставит их без изменения, Т.е.
 .
Векторы
.
Векторы
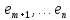 ортогональны
каждому из векторов
ортогональны
каждому из векторов
 базиса
линейного подпространства
базиса
линейного подпространства
 и,
следовательно, ортогональны так как
и,
следовательно, ортогональны так как
 .
Поэтому все они попадают в ортогональное
дополнение
.
Поэтому все они попадают в ортогональное
дополнение
 .
.
Рассмотрим
произвольный вектор
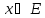 и запишем его разложение
по базису е:
и запишем его разложение
по базису е:

Легко
увидеть, что
 есть вектор из
есть вектор из
 ,
а
,
а
 есть
вектор из
есть
вектор из
 .,
при
этом
.,
при
этом
 .
Следовательно,
.
Следовательно,
 ,
и
так как вектор x
выбирался
произвольно, то
,
и
так как вектор x
выбирался
произвольно, то
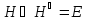 .
.
Согласно
следствию из теоремы 2.5, из соотношения
 вытекает следующее равенство для
размерностей:
вытекает следующее равенство для
размерностей:
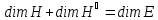
Что и требовалось доказать.
Следствие
3.1. Каково
бы ни было линейное подпространство
 в
евклидовом пространстве
в
евклидовом пространстве
 ,
любой вектор
,
любой вектор
 можно
однозначно представить в виде
можно
однозначно представить в виде
 (3.11)
(3.11)
где
 .
.
Действительно,
это утверждение означает, что
 .
.
Вектор
 в
разложении (3.11) называют ортогональной
проекцией вектора
х
на
линейное подпространство
в
разложении (3.11) называют ортогональной
проекцией вектора
х
на
линейное подпространство
 ,
а
вектор
,
а
вектор
 — ортогональной составляющей вектора
х
относительно
линейного подпространства
— ортогональной составляющей вектора
х
относительно
линейного подпространства
 .
.
Как
построить ортогональное дополнение к
данному линейному подпространству?
Пусть линейное подпространство
 определено
наиболее распространенным способом —
как линейная
оболочка некоторой
системы
векторов
определено
наиболее распространенным способом —
как линейная
оболочка некоторой
системы
векторов
 .
Согласно
определению 3.8 ортогонального дополнения,
любой вектор
.
Согласно
определению 3.8 ортогонального дополнения,
любой вектор
 должен
быть ортогонален каждому из векторов
должен
быть ортогонален каждому из векторов

 (3.12)
(3.12)
Наоборот,
если вектор х
удовлетворяет
системе равенств (3.12), т.е. он ортогонален
каждому из векторов
 ,
то этот вектор ортогонален и любой
линейной
комбинации системы
векторов
,
то этот вектор ортогонален и любой
линейной
комбинации системы
векторов
 (см.
3.5).
Значит,
х
ортогонален
каждому вектору линейного подпространства
(см.
3.5).
Значит,
х
ортогонален
каждому вектору линейного подпространства
 и
принадлежит линейному подпространству
и
принадлежит линейному подпространству
 .
.
Итак,
система уравнений (3.12) описывает
ортогональное дополнение линейного
подпространства
 .
Запишем
эту систему в координатах в некотором
ортонормированном базисе
.
Запишем
эту систему в координатах в некотором
ортонормированном базисе
 .
Пусть
векторы
.
Пусть
векторы
 в этом базисе имеют разложения
в этом базисе имеют разложения
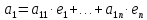
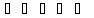



Координаты
произвольного вектора х
в
том же базисе обозначим
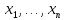 ,
т.е.
полагаем, что
,
т.е.
полагаем, что

Тогда в ортонормированном базисе е

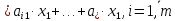
Таким образом, система (3.12), записанная в координатах относительно ортонормированного базиса е, имеет вид

 (3.13)
(3.13)
 ,
,
т.е.
представляет собой однородную систему
из т
линейных
алгебраических уравнений с п
неизвестными.
Строки матрицы А
этой
системы совпадают с наборами координат
векторов
 .
Поэтому
матрица А
имеет
ранг, равный рангу системы векторов
.
Поэтому
матрица А
имеет
ранг, равный рангу системы векторов
 ,
т.е.
этот ранг совпадает с размерностью
линейного подпространства
,
т.е.
этот ранг совпадает с размерностью
линейного подпространства
 .
.
Каждое
решение системы (3.13) представляет собой
набор координат некоторого вектора из
 -
и
наоборот, любой вектор из
-
и
наоборот, любой вектор из
 описывает
решение системы (3.13). Поэтому можно
сказать, что множество всех решений
этой системы есть линейное подпространство
описывает
решение системы (3.13). Поэтому можно
сказать, что множество всех решений
этой системы есть линейное подпространство
 .
Согласно
теореме 3.6, это подпространство имеет
размерность
.
Согласно
теореме 3.6, это подпространство имеет
размерность
 Множество
решений однородной системы линейных
алгебраических уравнений (СЛАУ)
описывается при помощи фундаментальной
системы решений. Напомним,
что столбцы фундаментальной системы
решений линейно независимы, а любое
решение однородной СЛАУ представляется
в виде линейной комбинации столбцов
фундаментальной системы решений. Другими
словами, фундаментальная система решений
— это базис в подпространстве всех
решений данной однородной СЛАУ. Каждый
столбец фундаментальной системы решений
представляет собой координатную запись
вектора линейного подпространства
Множество
решений однородной системы линейных
алгебраических уравнений (СЛАУ)
описывается при помощи фундаментальной
системы решений. Напомним,
что столбцы фундаментальной системы
решений линейно независимы, а любое
решение однородной СЛАУ представляется
в виде линейной комбинации столбцов
фундаментальной системы решений. Другими
словами, фундаментальная система решений
— это базис в подпространстве всех
решений данной однородной СЛАУ. Каждый
столбец фундаментальной системы решений
представляет собой координатную запись
вектора линейного подпространства
 в
выбранном базисе е
евклидова
пространства
в
выбранном базисе е
евклидова
пространства
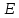 ,
при этом такие векторы в совокупности
образуют базис подпространства
,
при этом такие векторы в совокупности
образуют базис подпространства
 .
Мы
здесь можем не различать фундаментальную
систему решений системы (3.13) и
соответствующий ей базис ортогонального
дополнения
.
Мы
здесь можем не различать фундаментальную
систему решений системы (3.13) и
соответствующий ей базис ортогонального
дополнения
 .
.
Пример
3.16. Пусть
линейное подпространство
 представляет
собой линейную оболочку системы векторов,
заданных координатами в некотором
фиксированном ортонормированном базисе
е
четырехмерного
евклидова пространства
представляет
собой линейную оболочку системы векторов,
заданных координатами в некотором
фиксированном ортонормированном базисе
е
четырехмерного
евклидова пространства
 :
:
 ,
, 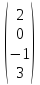 ,
,  ,
,  .
.
Найдем
какой-либо базис ортогонального
дополнения
 .
.
Записываем
систему вида (3.13), используя координаты
векторов


и
находим ее фундаментальную систему
решений. Это можно сделать, например, с
помощью приведения матрицы системы к
ступенчатому виду методом элементарных
преобразований. В качестве базисных
переменных выберем
 и
и
 Тогда фундаментальная система решений
будет содержать два решения, например:
Тогда фундаментальная система решений
будет содержать два решения, например:
 ,
, 
Столбцы
найденной фундаментальной системы
решений представляют собой координаты
двух векторов
 ,
,
 из
из
 ,
образующих базис линейного подпространства
,
образующих базис линейного подпространства
 ,
но
этот базис не является ортонормированным.
Чтобы получить ортонормированный базис
,
но
этот базис не является ортонормированным.
Чтобы получить ортонормированный базис
 ,
достаточно применить процесс
ортогонализации Грама
—
Шмидта. Сделав это, находим векторы
,
достаточно применить процесс
ортогонализации Грама
—
Шмидта. Сделав это, находим векторы



и
ортонормированный
базис в линейном пространстве
 .
.

