
re / Лекция 8
.docx4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ
4.1. Определение линейного оператора.
Оператором,
действующим в линейном пространстве
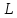 (или преобразованием
линейного пространства
(или преобразованием
линейного пространства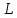 )
называется правило
)
называется правило
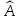 ,
по которому каждому элементу х
из
,
по которому каждому элементу х
из
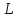 ставится в соответствие некоторый
(единственный) элемент у
из
ставится в соответствие некоторый
(единственный) элемент у
из
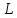 ..
Элемент у
называется образом
элемента х
при действии оператора
..
Элемент у
называется образом
элемента х
при действии оператора
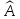 ,
а элемент х
— прообразом
элемента у.
Тот факт, что элемент у
соответствует элементу х
при действии оператора
,
а элемент х
— прообразом
элемента у.
Тот факт, что элемент у
соответствует элементу х
при действии оператора
 записывается
так:
записывается
так:
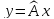 или
или
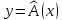 (1)
(1)
Определение
4.1.
Оператор
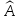 ,
действующий в линейном пространстве
,
действующий в линейном пространстве
 ,
называется линейным,
если для любых элементов
,
называется линейным,
если для любых элементов
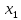 и
и
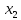 из
из
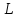 и любого числа
и любого числа
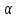 выполняются
равенства:
выполняются
равенства:

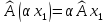 (2)
(2)
Примеры линейных операторов.
1)
Нуль-оператор
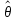 ставит в соответствие каждому элементу
х
из
ставит в соответствие каждому элементу
х
из
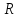 нулевой элемент
нулевой элемент
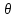 :
:
 .
.
2)
Тождественный
или единичный
оператор
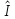 каждому
элементу х
из
каждому
элементу х
из
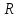 сопоставляет этот же элемент:
сопоставляет этот же элемент:
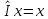 .
.
3)
Оператор
подобия
с коэффициентом подобия
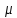 задается равенством
задается равенством
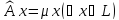 .
.
4)
Оператор
дифференцирования
 ,
действующий
в линейном пространстве Рп
многочленов
степени, не превосходящей
n,
каждому
многочлену
,
действующий
в линейном пространстве Рп
многочленов
степени, не превосходящей
n,
каждому
многочлену
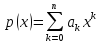 ставит в соответствие его производную
ставит в соответствие его производную
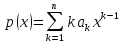 :
:
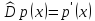 (заметим,
что
(заметим,
что
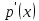 является
элементом
того же пространства Рп).
является
элементом
того же пространства Рп).
5)
Оператор
поворота
на угол
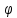 ,
действующий в пространстве
,
действующий в пространстве
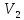 векторов на плоскости, поворачивает
каждый вектор на угол
векторов на плоскости, поворачивает
каждый вектор на угол
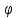 ,
причем поворот происходит против часовой
стрелки, если
,
причем поворот происходит против часовой
стрелки, если
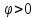 ,
и по часовой стрелке, если
,
и по часовой стрелке, если
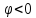 .
.
4.2.
Матрица линейного оператора. Пусть
 — линейный оператор, действующий в
линейном пространстве
— линейный оператор, действующий в
линейном пространстве
 ,
и пусть
,
и пусть
 — базис в этом пространстве. Подействуем
оператором
— базис в этом пространстве. Подействуем
оператором
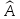 на базисные элементы и разложим образы
базисных элементов
на базисные элементы и разложим образы
базисных элементов
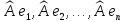 по тому же базису:
по тому же базису:
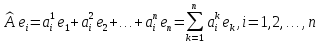 (3)
(3)
Квадратная
матрица п-го
порядка
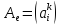 называется матрицей
линейного оператора
называется матрицей
линейного оператора
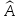 в базисе
в базисе
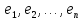 .
Отметим, что i-й
столбец матрицы
.
Отметим, что i-й
столбец матрицы
 составлен из коэффициентов
составлен из коэффициентов
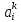 разложения элемента
разложения элемента
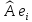 по базису
по базису
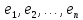 .
Равенства (3) можно записать в матричной
форме:
.
Равенства (3) можно записать в матричной
форме:
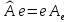 (3)
(3)
где,
как обычно, использованы обозначения:
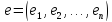 — строка, составленная из элементов
базиса,
— строка, составленная из элементов
базиса,
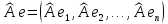 — строка из образов базисных элементов,
а произведение
— строка из образов базисных элементов,
а произведение
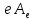 получается
по правилу умножения матриц:
получается
по правилу умножения матриц:
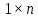 - матрица е
умножается на
- матрица е
умножается на
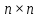 - матрицу
- матрицу
 .
.
Пусть
в базисе
 элемент х
и его образ
элемент х
и его образ
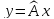 имеют разложения
имеют разложения
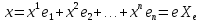 и
и
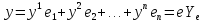
где
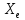 и
и
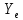 — столбцы из координат элементов x
и у
в данном базисе. Тогда из равенства
— столбцы из координат элементов x
и у
в данном базисе. Тогда из равенства
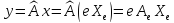 получаем
формулу
получаем
формулу
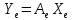 (4)
(4)
Формула
(4) позволяет определить координаты
образа у
через координаты прообраза х
в данном базисе, если известна матрица
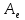 оператора
оператора
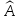 в этом базисе.
в этом базисе.
При
переходе к новому базису координаты
вектора
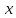 изменяются по формуле
изменяются по формуле
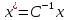 ,
а
координаты
вектора
,
а
координаты
вектора
 изменяются по формуле
изменяются по формуле
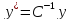 где
C
— матрица перехода от базиса
где
C
— матрица перехода от базиса
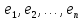 к базису
к базису
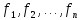 :
:
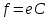 ,
состоящая из столбцов координат вектора
,
состоящая из столбцов координат вектора
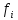 в старом
базисе е.
в старом
базисе е.
Тогда
 .
.
И
матрица
 оператора
оператора
 в базисе
в базисе
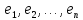 и матрица
и матрица
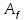 того же оператора в базисе
того же оператора в базисе
 связаны соотношением
связаны соотношением
 (5)
(5)
Матрицы, связанные между собой соотношениями (5) называют подобными.
Определение.
Операторы
 и
и
 ,
действующие в линейном пространстве
,
действующие в линейном пространстве
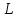 ,
называются равными,
если для
,
называются равными,
если для
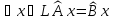 .
.
Если
операторы
 и
и
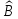 равны, то равны и их матрицы в любом
базисе. Обратно: если матрицы операторов
равны, то равны и их матрицы в любом
базисе. Обратно: если матрицы операторов
 и
и
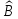 в каком-нибудь базисе равны, то равны и
сами операторы. Поэтому если в линейном
пространстве фиксирован базис
в каком-нибудь базисе равны, то равны и
сами операторы. Поэтому если в линейном
пространстве фиксирован базис
 ,
то между операторами, действующими в
этом пространстве, и квадратными
матрицами п-го
порядка имеет место взаимно однозначное
соответствие: каждому оператору
,
то между операторами, действующими в
этом пространстве, и квадратными
матрицами п-го
порядка имеет место взаимно однозначное
соответствие: каждому оператору
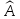 соответствует матрица
соответствует матрица
 и, обратно, каждой матрице А
соответствует (и притом только один)
оператор
и, обратно, каждой матрице А
соответствует (и притом только один)
оператор
 такой, что его матрица
такой, что его матрица
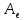 в базисе
в базисе
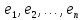 равна матрице
А.
равна матрице
А.
4.3. Действия над линейными операторами.
Определение.
Суммой
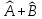 линейных операторов
линейных операторов
 и
и
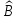 ,
действующих
в линейном пространстве
,
действующих
в линейном пространстве
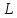 ,
называется оператор
,
называется оператор
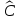 ,
действие которого на любой элемент х
из
,
действие которого на любой элемент х
из
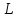 задается равенством
задается равенством
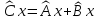 .
.
Сумма двух линейных операторов является линейным оператором, а матрица суммы линейных операторов (в любом базисе) равна сумме матриц этих операторов.
Определение.
Произведением
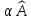 линейного оператора
линейного оператора
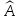 ,
действующего в линейном пространстве
,
действующего в линейном пространстве
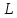 ,
на
число
,
на
число
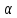 называется оператор
называется оператор
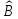 ,
действие которого на любой элемент x
из
,
действие которого на любой элемент x
из
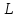 задается равенством
задается равенством
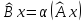
Произведение
линейного оператора
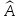 на
число
на
число
 является линейным оператором, а матрица
этого оператора (в любом базисе) равна
произведению матрицы оператора
является линейным оператором, а матрица
этого оператора (в любом базисе) равна
произведению матрицы оператора
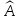 на
число
на
число
 .
.
Теорема
1.
Множество
S
всех линейных операторов, действующих
в линейном пространстве
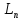 ,
с
введенными операциями сложения операторов
и умножения оператора на число образует
линейное пространство.
,
с
введенными операциями сложения операторов
и умножения оператора на число образует
линейное пространство.
Пространство
S
линейных операторов, действующих в
линейном пространстве
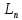 изоморфно пространству
изоморфно пространству
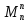 матриц размерности
матриц размерности
 .
Поэтому размерности этих пространств
совпадают, т. е.
.
Поэтому размерности этих пространств
совпадают, т. е.
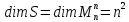 .
.
Определение.
Произведением
 линейных операторов
линейных операторов
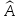 и
и
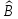 ,
действующих
в линейном пространстве
,
действующих
в линейном пространстве
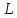 ,
называется оператор
,
называется оператор
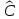 ,
действие которого на любой элемент x
из
,
действие которого на любой элемент x
из
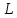 задается равенством
задается равенством

Произведение
линейных операторов
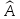 и
и
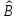 является линейным оператором, а матрица
С
произведения операторов (в любом базисе)
равна произведению матриц А
и В
этих операторов:
является линейным оператором, а матрица
С
произведения операторов (в любом базисе)
равна произведению матриц А
и В
этих операторов:
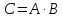 =.
=.
Определение.
Линейный оператор
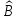 называется
обратным
к линейному оператору
называется
обратным
к линейному оператору
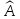 ,
если выполняются равенства
,
если выполняются равенства
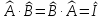 ,
где
,
где
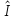 — тождественный оператор.
— тождественный оператор.
Оператор,
обратный к
 ,
обозначается символом
,
обозначается символом
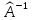 .
.
Теорема
2.
Для
того чтобы существовал обратный оператор
к линейному оператору
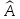 ,
необходимо
и достаточно,
чтобы
матрица оператора
,
необходимо
и достаточно,
чтобы
матрица оператора
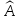 в
каком-нибудь базисе была невырожденной
(при
этом она будет невырожденной в любом
другом базисе).
в
каком-нибудь базисе была невырожденной
(при
этом она будет невырожденной в любом
другом базисе).
Если
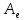 —
матрица оператора
—
матрица оператора
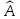 в базисе
в базисе
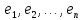 ,
то матрица обратного оператора
,
то матрица обратного оператора
 в том же базисе равна
в том же базисе равна
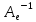 ,
т. е. является обратной по отношению к
матрице
,
т. е. является обратной по отношению к
матрице
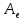 .
.
