
- •Кафедра теоретической и общей Электротехники
- •IiIкурса дневной и заочной формы обучения)
- •Содержание
- •1 Введение
- •2.3 Типовые примеры
- •2.4 Контрольные задания 1
- •1Расчет электростатического поля объемного заряда
- •2 Расчет электростатического поля двухпроводной
- •3 Электрическое поле постоянного тока в проводящей среде
- •3.1 Рабочая программа
- •3.2 Основные положения и соотношения
- •4 Магнитное поле постоянного тока
- •4.1 Рабочая программа
- •4.2 Основные положения
- •4.3 Типовые примеры
- •4.4 Контрольные задания 2
- •1 Расчет магнитного поля постоянного тока
- •5 Переменное электромагнитное поле
- •5.1 Рабочая программа
- •5.2 Основные положения и соотношения
- •5.3 Типовые примеры
- •5.4 Контрольные задания 3
- •1 Расчет электромагнитного поля в проводящей среде
- •Список рекомендуемой литературы
5 Переменное электромагнитное поле
5.1 Рабочая программа
Определение переменного электромагнитного поля. Основные уравнения (уравнение Максвелла) переменного электромагнитного поля. Уравнение непрерывности. Уравнение максвелла в комплексной форме записи. Теорема Умова-Пойнтинга для мгновенных значений и в комплексной форме записи. Переменное электромагнитное поле в однородной и изотропной проводящей среде. Уравнение Максвелла для проводящей среды. Магнитный поверхностный эффект. Электрический поверхностный эффект.
5.2 Основные положения и соотношения
1. Переменное электромагнитное поле
(ПЭМП) – совокупность изменяющихся во
времени и взаимно связанных и
обуславливающих друг друга электрического
и магнитного полей. Оно определяется
двумя векторными величинами –
напряженностью электрического поля
![]() и напряженностью магнитного поля
и напряженностью магнитного поля![]() .
.
2. Уравнения Максвелла. Исследование процессов ПЭМП осуществляют с помощью уравнения Максвелла. Систему уравнений Максвелла образуют четыре уравнения:
Первое уравнение Максвелла выражает связь между ротором напряженности магнитного поля и плотностью тока в той же точке поля. Для мгновенных значений первое уравнение Максвелла записывается следующим образом:
![]() .
.
В первой части уравнения имеются две
плотности тока: плотность тока проводимости
![]() и плотность тока смещения
и плотность тока смещения![]() .
Ток смещения возбуждает магнитное поле
так же, как и ток проводимости.
.
Ток смещения возбуждает магнитное поле
так же, как и ток проводимости.
При изменении Е и Н во времени по синусоидальному закону можно воспользоваться символическим методом и записать первое уравнение Максвелла в комплексной форме записи
![]() .
.
Второе уравнение Максвелла определяет связь между ротором напряженностью электрического поля и скоростью изменения магнитного поля в той же точке поля. Для мгновенных значений оно записывается следующим образом:
![]() ,
,
т.е. всякое изменение магнитного поля
во времени
![]() в какой-либо точке поля возбуждает
вихрь электрического поля в той же точке
поля.
в какой-либо точке поля возбуждает
вихрь электрического поля в той же точке
поля.
В комплексной форме записи второе уравнение Максвелла имеет вид
![]() .
.
Уравнение
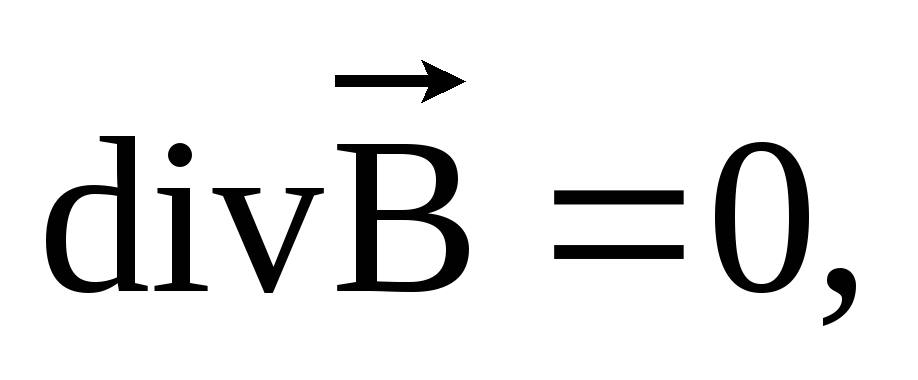 выражающее принцип непрерывности
магнитного поля.
выражающее принцип непрерывности
магнитного поля.Уравнение
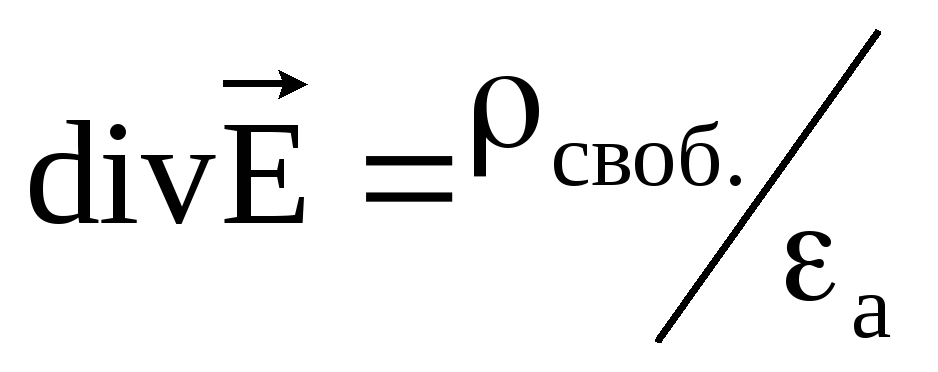 выражает связь между истоком напряженности
электрического поля и плотностью
свободных зарядов в той же точке поля.
выражает связь между истоком напряженности
электрического поля и плотностью
свободных зарядов в той же точке поля.
3.Уравнение непрерывности. Линии полного
тока
![]() являются непрерывны, т.е. на границе
проводящей среды и диэлектрика ток
проводимости переходит в ток смещения.
Уравнение непрерывности записывается
следующим образом:
являются непрерывны, т.е. на границе
проводящей среды и диэлектрика ток
проводимости переходит в ток смещения.
Уравнение непрерывности записывается
следующим образом:
![]() .
.
Это уравнение можно записывать иначе
![]() .
.
Это уравнение также называют законом сохранения заряда. Этот закон означает, что электрический заряд неуничтожим, он может только перемещаться из одного места в другое.
4. Теорема Умова-Пойнтинга.
Теорема Умова-Пойнтинга описывает энергетические соотношения в поле. Она имеет две формы записи: первая – для мгновенных значений, вторая – комплексная фора – для синусоидально изменяющихся величин.
Теорема Умова-Пойнтинга для мгновенных значений записывается следующим образом:
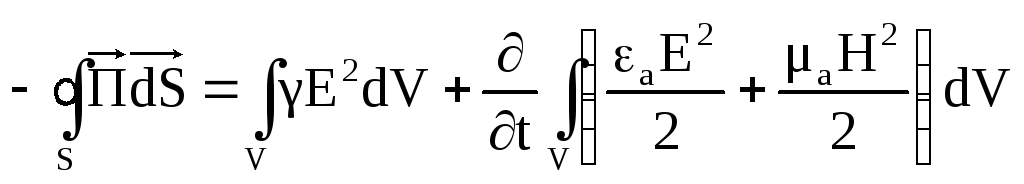 .
.
Левая часть уравнения есть поток вектора
Пойнтинга
![]() (направленный внутрь объема) сквозь
любую замкнутую поверхностьS,
ограничивающую некоторый объемV.
Размерность вектора Пойнтинга равна
произведению размерности Е и Н, т.е.
(направленный внутрь объема) сквозь
любую замкнутую поверхностьS,
ограничивающую некоторый объемV.
Размерность вектора Пойнтинга равна
произведению размерности Е и Н, т.е.
![]() .
.
Правая часть уравнения есть энергия
![]() ,
выделяющаяся в виде теплоты в единицу
времени в объемеV; и
,
выделяющаяся в виде теплоты в единицу
времени в объемеV; и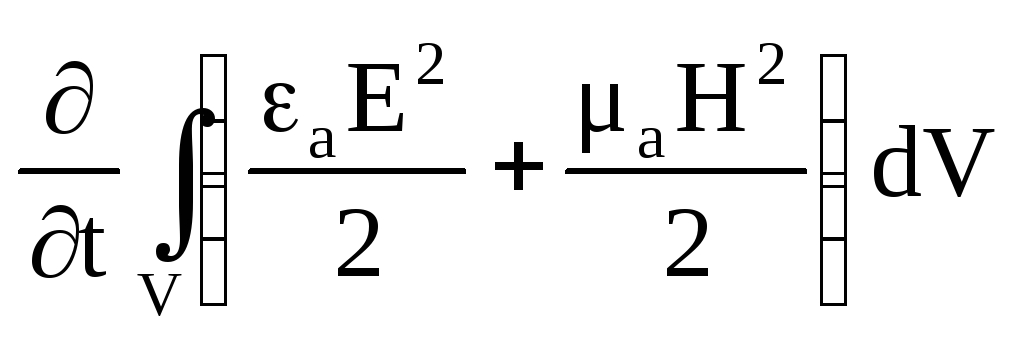 есть скорость изменения запаса
электромагнитной энергии в данном
объеме.
есть скорость изменения запаса
электромагнитной энергии в данном
объеме.
Теорема Умова-Пойнтинга в комплексной форме записи имеет вид:
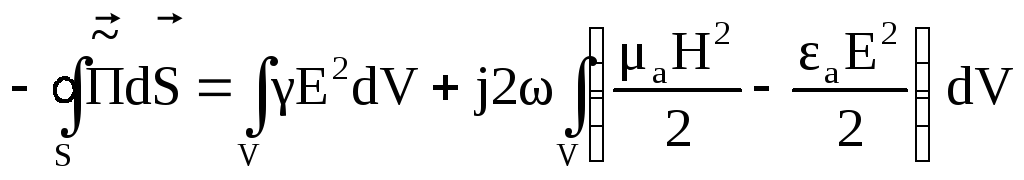 .
.
Первое слагаемое правой части – активная мощность, второе – реактивная. Следовательно, теорему Умова-Пойнтинга можно записать следующим образом:
![]() .
.
В последних выражениях
![]() – комплексный вектор Пойнтинга.
– комплексный вектор Пойнтинга.
5. Уравнения Максвелла для проводящей среды.
![]() ,
,![]() .
.
6. Плоская электромагнитная волна.
Под плоской электромагнитной волной
понимают волну, векторы![]() которой
расположены в плоскостиxoy,
перпендикулярной направлению
распространения волны (осьz)
и изменяющиеся только в функции координатыzи времениt.
которой
расположены в плоскостиxoy,
перпендикулярной направлению
распространения волны (осьz)
и изменяющиеся только в функции координатыzи времениt.
Напряженность магнитного поля определяется:
![]() ,
,
где
![]() – постоянные интегрирования, которые
определяются из граничных условий:
– постоянные интегрирования, которые
определяются из граничных условий:![]() .
.
Напряженность электрического поля равна:
![]() ,
,
где
![]() – волновое сопротивление.
– волновое сопротивление.
7. Глубина проникновения и длина волны.
Под глубиной проникновения ∆ понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшится в е = 2,71 раз. Учитывая, что е-К∆ = е-1, получим
![]() .
.
Под длиной волны λ в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2π. Учитывая, что λ · κ = 2π, получим
![]() .
.
Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу:
![]() .
.
8. Магнитный поверхностный эффект.
Явление неравномерного распределения поля по сечению проводящего тепла, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, при условии, что вдоль листа направлен магнитный поток, называют поверхностным магнитным эффектом. В этом случае:
![]() ,
,
![]() .
.
Если считать
![]() ,
то напряженность поля на поверхности
листа можно определить
,
то напряженность поля на поверхности
листа можно определить
![]() .
.
9. При электрическом поверхностном эффекте вдоль пластины (шины) направлен синусоидальный ток частоты ω. в этом случае поле внутри пластины определяется по формулам:
![]() ,
,![]() ,
,![]() .
.
