Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский Государственный аграрно-технологический университет им. Д.Н. Прянишникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика

..pdf

Скачиваний:

Добавлен:

06.02.2016

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

10 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Пример	34.	Решить	дифференциальное		уравнение

(2х у) у х 2у .
Решение.	Запишем уравнение в виде y f (x, y).				Для этого
разделим обе его части на (2х у).
			õ 2 ó
		ó		.
		ó	( 2õ ó )	.
Проверим функцию f(x, y) на однородность:
f (tx, ty)	tх 2tу	f (x, y).
f (tx, ty)	2tх уt	f (x, y).
	2tх уt

Следовательно, функция f(x, y) – однородная нулевого измерения, а данное уравнение – однородное.

Введем вспомогательную функцию u.

u x ;

y ux;

y u x u .

Тогда данное уравнение примет вид:

х 2ux

1 2u

u x u

, u x u

u x

2х ux

2 u

1 2u 2u u2

1 u2

2 u

x 2 u

u x

, u

1 u2

Так как

dx u

, то dx x 2 u

Разделяем переменные:

2 u du

1 u2

Интегрируя, получаем: ln

u 1

1 u2

ln C

u 1

Преобразуем

u 1

1 u2

или

u 1

1 u2

Переходя от вспомогательной функции обратно к функции у: u xy , получаем общий интеграл данного уравнения:

		y		1
		x		1	Cx.
		x

y				y 2
	1		1
	1		1
x				x

Пример 35. Найти частное решение дифференциального уравнения

у 2xу 3х2e x2 .

Решение. Это линейное дифференциальное уравнение первого порядка, так как оно имеет вид

y p(x) y q(x).

Делаем замену y = uv, y u v uv . Получаем

u v uv 2uvx 3х2e x2 u v u(v 2vx) 3х2e x2

Функцию v=v(x) найдём из условия равенства 0 выражения в скобках

2vx =0

Так как dx v

, тогда dx 2vx

Разделим переменные и проинтегрируем

2xdx

ln v x2 C

Положим С=0, тогда

v e x2

Подставим

заданную

функцию в

дифференциальное уравнение

u v u(v 2vx) 3х

и получим u e

3х

u 3х2

3х2 du 3х2dx

Так как dx

, то

Проинтегрируем

du 3х2dx u х3 C

Таким образом

y vu e x2 x3 C - общее решение линейного уравнения.

Пример 36. Найти общее решение дифференциального уравне-

ния y 2 у 3y хе х

Решение. Дано линейное дифференциальное уравнение второго

порядка с постоянными коэффициентами. Его общее решение имеет вид

у y0 у

где y0 - общее решение соответствующего линейного однородного уравнения, у - частное решение линейного неоднородного уравнения.

Соответствующее линейное однородное уравнение y 2у 3y 0

Составим и решим характеристическое уравнение:


k 2 2k 3 0;	k 2 i 2,	k	2	2 i 2.
	1		2

Корни характеристического уравнения комплексные:

k1 i,	k2 i.
		2,	2.

В этом случае общее решение линейного однородного уравнения имеет вид:

y e x (С1 cos x С2 sin x).

Таким образом, получили:

y0 e2 x (С1 cos 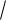2x С2 sin 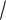2x).

Частное решение y линейного неоднородного уравнения под-

бираем по виду правой части	f (x) хе х
y xr e xQ(x)	1;	Q(x) Ах В;

а r – число корней характеристического уравнения равных γi. В нашем случае

k1 2 i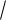2 1i, k2 2 i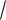2 1i, следовательно, r=0. y ( Аx В)e x .

Воспользуемся методом неопределенных коэффициентов. y Аe x ( Аx В)e x.

y Аe x Аe x ( Аx В)e x.

Подставляя в исходное уравнение y , y , y , получаем:

2Аe x (Аx В)e x 2Аe x 2(Аx В)e x 3( Аx В)e x xe x

Преобразуем его

2А Аx В 2А 2Аx 2В 3Аx 3В x

4А 6Аx 6В x

Приравниваем коэффициенты при одинаковых степенях переменной в левой и правой частях уравнений

х0	4А 6В 0
х0	4А 6В 0
х1	6А 1
Получаем систему уравнений
			1
4А 6В 0		A
4А 6В 0		A	6
	6А 1		6
			1
			1
		B
		B	9

		1		1
Частное решение имеет вид	y		x		e x .
Частное решение имеет вид	y		x		e x .
	6			9

Общее		решение	линейного				неоднородного уравнения:
				1		1

y e2 x (С cos	2x С sin		2x)		x		e x .
						9
1	2			6

Контрольные вопросы

1.Физические задачи, приводящие к дифференциальным уравне-

ниям.

2.Дифференциальные уравнения: основные понятия.

3.Дифференциальные уравнения первого порядка: теорема и задача Коши.

4.Дифференциальные уравнения первого порядка с разделяющимися переменными.

5.Однородные дифференциальные уравнения первого порядка.

6.Дифференциальные уравнения первого порядка: линейные, Бер-

нулли.

7.Дифференциальные уравнения второго порядка: общие понятия, уравнения допускающие понижение порядка.

8.Линейные дифференциальные уравнения второго порядка.

9.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

10.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

11 Ряды

Пример 37. Исследовать на сходимость с помощью признака

Даламбера положительный ряд 3n 2 .

n 1

Решение. Применяем признак Даламбера:

un 1

n 1

(n 1)3n 2

n 1

lim

3n 3

lim

n3n 3

3n 2

Получаем, что этот ряд сходится по признаку Даламбера, так как

un 1

lim

Пример 38. Найти интервал сходимости ряда и исследовать его

сходимость на концах интервала:

n 0

n 2

Решение. Используя признак Даламбера найдём предел

4n 1 xn 1

4n 1 xn 1(n 2)

lim

an 1

lim

n 3

lim

4n xn

4n xn (n 3)

n 2

lim

4 x(n 2)

n 3

Определяем при каких значениях х этот предел будет меньше едини-

					1			1		1
цы:	4x	<1,	х	<		,	-		<х<		, следовательно, согласно признаку
					4			4		4

Даламбера, при любых значениях х из найденного интервала сходи-

мости ряд сходится абсолютно, а при х > 14 расходится. В граничных

точках интервала х=± 14 предел равен 1, в них признак Даламбера не даёт ответа на вопрос о сходимости ряда.

При х=- 14 получаем числовой знакочередующийся ряд

	1
( 1)n		.

n 0	n 2

Составим ряд из абсолютных величин членов ряда

1+	1	+	1	+	1	+… +	1	...
	2		3		4		n 2

Его члены образуют монотонно убывающую последовательность, а общий член стремится к нулю un 0 , следовательно, знакочередующийся ряд сходится по признаку Лейбница.

				1													1
При х=				1		получаем ряд с положительными членами											1	.
При х=						получаем ряд с положительными членами												.
	4															n 0 n 2
Используем признак сравнения. Сравним полученый ряд с гар-
моническим рядом
	1
									n 1		1.
lim	n 2				lim				n 1
lim					lim
n		1					n n 2
		n 1
												1
Т.к. 1≠0, а гармонический ряд												1	расходится, то расходится
Т.к. 1≠0, а гармонический ряд													расходится, то расходится
											n 0 n 1
	1
и ряд	1		.
и ряд			.
n 0 n 2
																4n xn
Следовательно, областью сходимости ряда																	является
Следовательно, областью сходимости ряда																n 2	является
															n 0	n 2
промежуток -					1		≤х<	1		.
промежуток -					4		≤х<	4		.
					4			4
								1						x
Пример 39. Вычислить интеграл х sin														x	dx с точностью до 0,001.
Пример 39. Вычислить интеграл х sin													3		dx с точностью до 0,001.
								0					3
								0

Решение. Т.к. интегрирование производится в окрестности точки х=0, то можно воспользоваться для разложения в ряд подынтегральной функции формулой Маклорена.

Разложение в ряд функции sin x имеет вид:

n 1 x

2n 1

n 1

2n 1

sin x x

... ( 1)

… ( 1)

(2n 1)!

n 1

Используя это разложение, запишем разложение в ряд функции sin 3x :

sin

... ( 1)n 1

x2n 1

243 5!

32n 1(2n 1)!

2n 1

... ( 1)n 1

32n 1(2n 1)!

n 1

Теперь представим в виде ряда подынтегральную функцию:

х sin		x						x2			x4							x6			... ( 1)n 1									x2n
х sin																					... ( 1)n 1
		3				3					27 3!				243 5!												32n 1(2n 1)!
														x		2n
...						( 1)n 1								x

												32n 1(2n 1)!
		n 1										32n 1(2n 1)!
		Получаем данный интеграл в виде:
1			x							1												x	2n				1			x	2		x	4		x		6
õ sin			x		dx						( 1)n 1											x				dx			(	x			x			x			...)dx
õ sin					dx						( 1)n 1								2n 1							dx			(			27 3!				243 5!			...)dx
0				3						0 n 1								3				( 2n 1)!					0		3			27 3!				243 5!
	x	3							x	5						x		7						1	3				5						7
		3								5								7							3				5						7
																									1				1					1

																				...																	...
	3 3							27 3! 5					243 5! 7											0	3 3			27 3! 5					243		5! 7
	0	3				0				5					0		7
	0					0									0									0,1111			0,0012 0,000004 0,109.

																						...
	3 3						27 3! 5						243 5! 7

Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения.

Контрольные вопросы

1.Перечислите свойства сходящихся рядов.

2.Каково необходимое условие сходимости ряда, его следствие.

3.Сформулируйте 1-ый, 2-ой признаки сравнения, признак Даламбера, интегральный признак Коши.

4.Дайте определение знакочередующегося ряда.

5.Сформулируйте признак Лейбница.

6.Дайте определение абсолютной и условной сходимости ряда.

7.Что называется интервалом сходимости степенного ряда?

8.Сформулируйте необходимое и достаточное условие разложимости функции в степенной ряд.

Контрольная работа №2

В задачах 1-20 найти экстремум функции.

1.z 4х2 5y2 6xy 6x 2 y 54;

2.z 6х2 2 y2 2xy 8x 9 y 69;

3.z 5х2 5y2 4xy 6x 2 y 62;

4.z х2 4 y2 9xy x 3y 4;

5.z 7х2 3y2 xy 5x 8y 84;

6.z 7х2 5y2 5xy 6x 2 y 4;

7.z 9х2 4 y2 8xy 2x 7 y 5;

8.z 3х2 2 y2 xy 6x 2 y 12;

9.z х2 y2 2xy 3x 4 y 16;

10.z 6х2 7 y2 9xy 2x 3y 20;

11.z 2х2 3y2 8xy 3x 7 y 14;

12.z 10х2 14 y2 5xy 2x 6 y 12;

13.z 9х2 2 y2 4xy 4x 9 y 40;

14.z х2 3y2 8xy 3x 4 y 24;

15.z 4х2 5y2 6xy 6x 2 y 4;

16.z 5х2 5y2 9xy 7x 3y 30;

17.z 3х2 7 y2 2xy 7x 3y 6;

18.z х2 8y2 3xy 2x 3y 23;

19.z 6х2 9 y2 2xy 4x 4 y 32;

20.z х2 6y2 6xy 8x 2y 8.

Взадачах 21-40 изменить порядок интегрирования, найти интеграл при заданном и изменённом порядке интегрирования.

21.	22.
23.	24.

25.	26.

	57

27.		28.
29.		30.
31.		32.
33.		34.

35.		36.

37.		38.
39.		40.

В задачах 41–60 решить дифференциальное уравнение.
41.	е2х 1 y ye2x 0.				42.	(2 y) (2 x) y 0.
43.	x2 y ( y 1) 0 .				44.	y ех 1 y ex 0 .
45.	ех 2 y yex .				46.	y ex y .
47.	xyy	3x	2	.	48.
						y tgx y 0.
49.	(1 x2 ) y 1 y2 .				50.	y cos x y sin x 0 .
51.	xy y x3 .				52.	xy y 2ln x .
53.	x3 y 3x2 y 2 .				54.	y ex y e2x .
55.	xy y x 1.				56.	y y cos x sin 2x .
57.	xy y 5x 9.				58.	y 4xy 4x3 .
59.	2xy y 2x3 .				60.	y xy x3 .

В задачах 61–80 найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными

коэффициентами.
61.	y 3y 2 y ex	62.	y 5y 2x3
		58

63.	y 5y 6y 13sin 3x	64.	y 2 y 3y 3ex
65.	y 2 y 2x 1	66.	2 y 4 y 5y 4e x
67.	y y 2x3 x 2	68.	4 y y 9 y sin x
69.	y 4 y 6 y 2x2	70.	y 2 y 2 y 8ex
71.	y 4 y 8x3	72.	3y 4 y cos x
73.	y 2 y y 8ex	74.	y 2 y 4 y 5ex
75.	y 2 y 5y 4e x	76.	3y y 2y 4sin 2x
77.	y 6 y 9y 10sin x	78.	y 4 y 2x 2
79.	y 9y cos 3x	80.	3y y x3 1

В задачах 81-100 исследовать на сходимость с помощью признака Даламбера положительный ряд

		2		n
81.		2
81.				5
	n 1 n			5
	n 1 n
				3			n
83.				3
83.			n 1 !
	n 1		n 1 !
		3		n		n!
85.		3				n!
85.			n		n
	n 1				n
	n 1
			n	n
87.			n
87.
	n 1		n!
89.			n 1 n / 2
89.								n!
	n 1							n!
				n
91.		2
91.		2
	n 1 n
				5				n
93.				5
93.		n 7 !
	n 1	n 7 !
			42n n!
95.
95.					2n

2n4n

97.n 1 !

n1 n

82.

2 n

n 1

2n n 1

84.

n 1

86.

n 1 !

n 1

88.

2n 1 5n

n 1

90.

n 1 n 2

n 1

92.

n 1

n n 1

94.

n 1

96.

2n 3 !

n 1

98.

n 1 23n

n 1

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.02.201664.21 Кб9матан 1-10.docx
#
06.02.2016439.62 Кб2матан 5.rtf
#
26.09.2019296.03 Кб0матан с 28-42.docx
#
06.02.2016461.38 Кб13Математика Д/З.doc
#
06.02.20161.52 Mб24Математика Шумаев В В.pdf
#
06.02.20161.35 Mб41Математика..pdf
#
06.02.2016303.1 Кб31Математическое моделирование и проектирование.doc
#
06.02.201610.17 Mб540машины для внесения минеральных удобрений.pdf
#
06.02.201619.02 Mб746машины для внесения органических удобрений.pdf
#
21.11.20197.09 Mб162Машины для основной обработки почвы.doc
#
06.02.2016473.02 Кб172машины для поверхностной обработки почвы.pdf