Инд.зад.9,10,11 сокращ
..docx-
Задание 4. Вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах, сделать чертеж.
-
r=4 cos 3
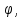 r=2(r
r=2(r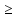 2).
2). -
r=cos2
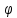
-
r=
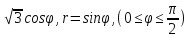
-
r=4sin3
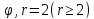
-
r=cos
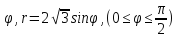
-
r=sin3
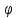
-
r=6sin3
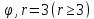
-
r=cos3
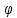
-
r=cos
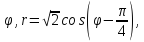 (
(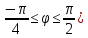
-
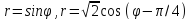 ,(
,(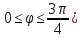
-
r=6cos3

-
r=
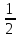 +sin
+sin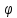
-
r=cos
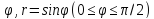
-
r=
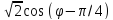 ,(
,(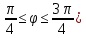
-
r=cos
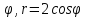
-
r=sin
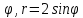
-
r=1+
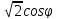
-
r=1/2+cos
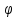
-
r=1+
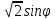
-
r=5/2+sin
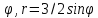
-
r=3/2cos
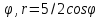
-
r=4cos4
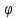
-
r=sin
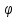
-
r=cos
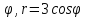
-
r=cos
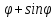
-
r=2sin4
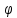
-
r=2cos6
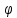
-
r=cos
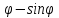
-
r=6sin
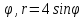
-
r=2sin
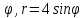
-
r=3sin
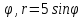
-
r=2cos
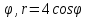
-
Задание 5. Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
-
y=lnx,
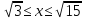
-
y=
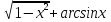 ,
0
,
0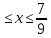
-
y=-ln cosx, 0
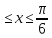
-
y=2+arcsin
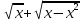 ,
,
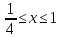
-
y=
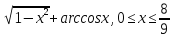
-
y=2+chx, 0
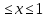
-
y=
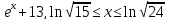
-
y=-arccos
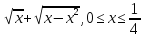
-
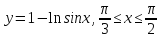
-
y=
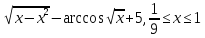
-
y=ln sin x,
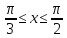
-
y=chx+3, 0
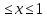
-
y=ln cosx+2, 0
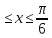
-
y=
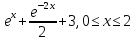
-
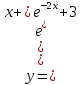
-
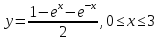
-
y=
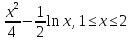
-
y=ln
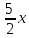 ,
,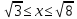
-
y=
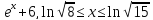
-
y=ln(
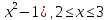
-
y=ln(1-
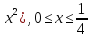
-
y=1-ln cos x, 0
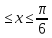
-
y=2-
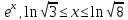
-
y=arcsinx-
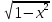 ,
0
,
0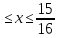
-
y=1-ln(
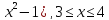
-
y=-arccosx+
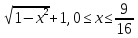
-
y=ln7-lnx,
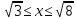
-
y=1+arcsinx-
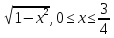
-
y=
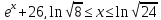
-
y=arccos
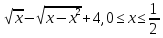
-
y=
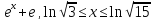
-
y=5-
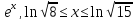
-
Задание 6. Вычислить длины дуг кривых, заданных параметрическими уравнениями.
-
x=5(t-sin t) y=5(1-cost) 0
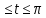
-
x=4(cost+t sint) y=4(sin t – t cos t) 0
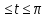
-
x=10
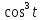 y=10
y=10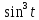 0
0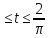
-
x=3(t+sin t) y=3(1 – cos t)
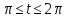
-
x=3(cost+t sint) y=3(cos t - t sin t) 0
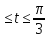
-
x=6
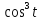 y=6
y=6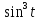 0
0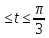
-
x=2,5(t+sint) y=2,5(1-cost)
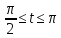
-
x=6(cost+t sint) y=6(sin t - t cost) 0
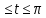
-
x=8
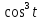 y=8
y=8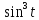 0
0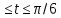
-
x=4(t – sin t) y=4(1 – cos t)
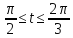
-
x=8(cos t+t sin t) y=8(sin t - t cos t) 0
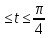
-
x=4
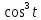 y=4
y=4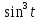
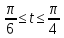
-
x=2(t – sin t) y=2(1 – cos t)
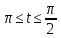
-
x=2(cos t+t sin t) y=(sin t - t cos t) 0
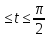
-
x=2
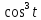 y=2
y=2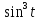 0
0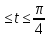
-
x=(
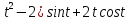 y=(2 -
y=(2 -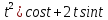 0
0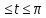
-
x=3(2cos t – cos 2t) y=3(2sin t – sin 2t) 0
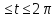
-
x=(
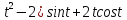 y=(2 -
y=(2 -
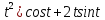 0
0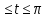
-
x=
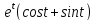 y=
y=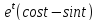 0
0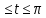
-
x=0,5(cos t – 0,25 cos2t) y=0,5(sin t – 0,25 sin2t)
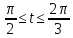
-
x=(
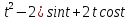 y=(2 -
y=(2 -
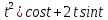 0
0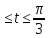
-
x=
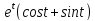 y=
y=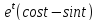
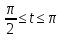
-
x=3,5(2cos t - cos2t) y=3,5(2sin t - sin2t) 0
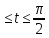
-
x=(
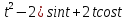 y=(2 -
y=(2 -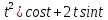 0
0
-
x=
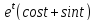 y=
y=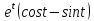 0
0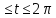
-
x=2(2cost - cos2t) y=2(2sin t - sin2t) 0
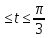
-
x=(
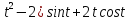 y=(2-
y=(2-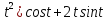 0
0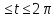
-
x=
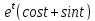 y=
y=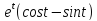 0
0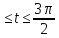
-
x=4(2cost - cos2t) y=4(2sin t – sin 2t) 0
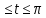
-
x=(
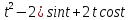 y=
y=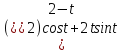 0
0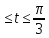
-
x=
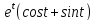 y=
y=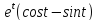
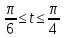
-
x=
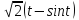
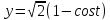
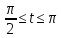
-
Задание 7. Вычислить длины дуг кривых, заданных уравнениями в полярных координатах.
-
r=3
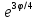 ,
,
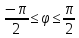
-
r=3

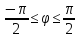
-
r=
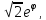
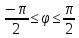
-
r=5
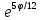 ,
,
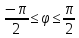
-
r=6
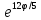 ,
,
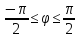
-
r=3
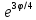 ,
,
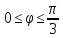
-
r=4
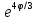 ,
,
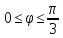
-
r=
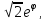
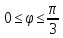
-
r=5
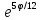 ,
,
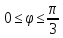
-
r=12
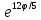 ,
,
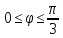
-
r=2(1-sin
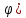 ,
,
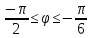
-
r=2(1-cos
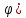 ,
,
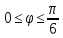
-
r=1+sin
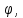
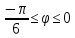
-
r=4(1-sin
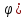 ,
,
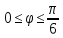
-
r=5(1-cos
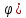 ,
,

-
r=6(1+sin
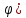 ,
,
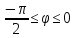
-
r=7(1-sin
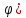 ,
,
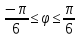
-
r=8(1-cos
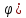 ,
,
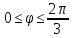
-
r=2
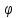 ,
,
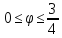
-
r=3(1-cos
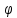 ),
),
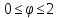
-
r=2
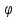 ,
,
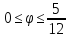
-
r=2
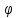 ,
,
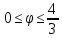
-
r=4
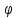 ,
,
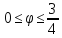
-
r=2
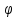 ,
,
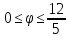
-
r=5
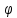 ,
,
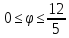
-
r=3
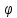 ,
,
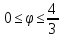
-
r=
 ,
,

-
r=2cos
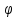 ,
,
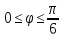
-
r=2sin
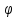 ,
,

-
r=6cos
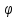 ,
,
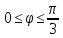
-
r=6sin
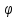 ,
,
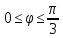
-
r=8sin
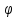 ,
,
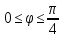
-
Задание 8. Вычислить объем тел, образованных вращением фигур, ограниченными графиками заданных функций. В вариантах 1- 16 ось вращения Ох, в вариантах 17-32 ось вращения Оy.
-
y=-
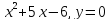
-
2x-х2-y=0, 2x2-4x+y=0
-
y=3sinx, y=sinx,0
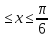
-
y=5cosx,y=cosx,x=0,x
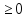
-
y=
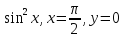
-
x=
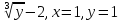
-
y=x
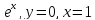
-
y=2x-
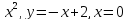
-
y=2x-
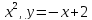
-
y=
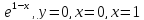
-
y=
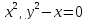
-
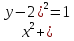
-
y=1-
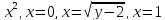
-
y=
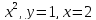
-
y=
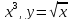
-
y=sin(
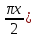 ,y=
,y=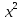
-
y=arcos
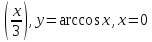
-
y=arcsin
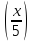 ,y=arcsin
,y=arcsin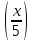
-
y=
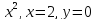
-
y=

-
y=
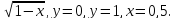
-
y=sin x, x=2,y=0
-
y=(x-1
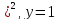
-
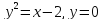 ,y=
,y=
-
y=
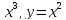
-
y=arccos
 ,y=arccos
,y=arccos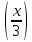 ,y=0
,y=0 -
y=arcsin x, y=arccos x, y=0
-
y=
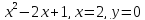
-
y=
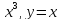
-
y=arcos x, y=arcsin x, x=0
-
y=(x-1
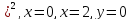
-
y=