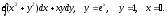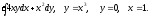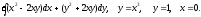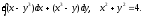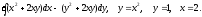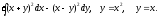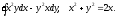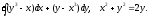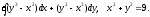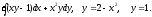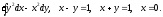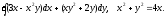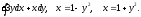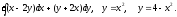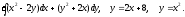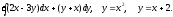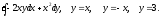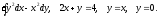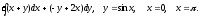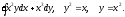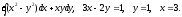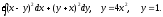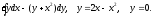Инд.зад.13, 14 кратн.и кривол.интегралы
.docx-
Задание 8. Вычислить тройной интеграл по области, ограниченной заданными поверхностями.
-
 ,
, -
Т: у = 10х, у = 0, х = 1,
-
z = xy, z = 0
-
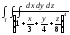 ,
, -
Т:
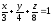 ,
, -
х = 0, у = 0, z = 0
-
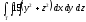 ,
, -
Т: z = х + y, у + x = 1,
-
х = 0, у = 0, z = 0
-
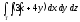 ,
, -
Т: у = х, у = 0, х = 1,
-
z = 5(x2 + y2), z = 0
-
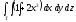 ,
, -
Т: у = 9х, у = 0, х = 1,
-
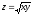 ,
z = 0
,
z = 0 -
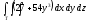 ,
, -
Т: у = х, у = 0, х = 1,
-
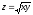 ,
z = 0
,
z = 0 -
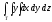 ,
, -
Т: у = 15х, у = 0, х = 1,
-
z = xy, z = 0
-
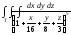 ,
, -
Т:
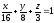 ,
, -
х = 0, у = 0, z = 0
-
 ,
, -
Т: z = 10y, у + x = 1,
-
х = 0, у = 0, z = 0
-
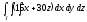 ,
, -
Т: z = х2 +3y2, у = x,
-
х = 8, у = 0, z = 0
-
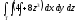 ,
, -
Т:
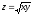 ,
у = x,
,
у = x, -
х = 1, у = 0, z = 0
-
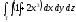 ,
, -
Т:
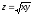 ,
у = 36x,
,
у = 36x, -
х = 1, у = 0, z = 0
-
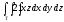 ,
, -
Т: у = х, у = 0, х = 2,
-
z = xy, z = 0
-
 ,
, -
Т:
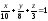 ,
, -
х = 0, у = 0, z = 0
-
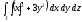 ,
, -
Т: z = 10x, у + x = 1,
-
х = 0, у = 0, z = 0
-
 ,
, -
Т: z = х2 +y2, у = x,
-
х = 1, у = 0, z = 0
-
 ,
, -
Т:
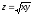 ,
у = 9x,
,
у = 9x, -
х = 1, у = 0, z = 0
-
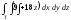 ,
, -
Т:
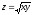 ,
у = 4x,
,
у = 4x, -
х = 1, у = 0, z = 0
-
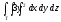 ,
, -
Т: у = 2х, у = 0, х = 2,
-
z = xy, z = 0
-
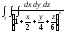 ,
, -
Т:
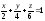 ,
, -
х = 0, у = 0, z = 0
-
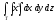 ,
, -
Т: z = 10(x+3y), у + x = 1,
-
х = 0, у = 0, z = 0
-
 ,
, -
Т: z = 3х2 +2y2, у = x,
-
х = 1, у = 0, z = 0
-
 ,
, -
Т:
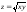 ,
у = x,
,
у = x, -
х = 1, у = 0, z = 0
-
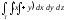 ,
, -
Т: z = 30х2 +60y2, у = x,
-
х = 1, у = 0, z = 0
-
 ,
, -
Т:
 ,
, -
х = 0, у = 0, z = 0
-
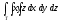 ,
, -
Т: z = хy, у = x,
-
х = 2, у = 0, z = 0
-
 ,
, -
Т: z = 10(3x+y), у + x = 1,
-
х = 0, у = 0, z = 0
-
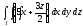 ,
, -
Т: z = х2 +15y2, у = x,
-
х = 1, у = 0, z = 0
-
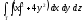 ,
, -
Т: z = 20(2x+y), у + x = 1,
-
х = 0, у = 0, z = 0
-
 ,
, -
Т:
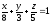 ,
, -
х = 0, у = 0, z = 0
-
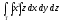 ,
, -
Т: z = хy, у = 3x,
-
х = 2, у = 0, z = 0
-
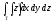 ,
, -
Т:
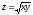 ,
у = 3x,
,
у = 3x, -
х = 2, у = 0, z = 0
-
-
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
-
Задание 1. Вычислить криволинейный интеграл первого рода вдоль линии Г между точками А и В.
-
 ,
Г: y
= ln x,
A(1, 0), B(e2,
2).
,
Г: y
= ln x,
A(1, 0), B(e2,
2). -
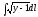 ,
Г: y
= x2
+ 1, A(0, 1), B(
,
Г: y
= x2
+ 1, A(0, 1), B(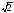 ,
3).
,
3). -
 ,
Г: y
= ln (x2
– 1), A(- 2, ln 2),
B(3, ln 8).
,
Г: y
= ln (x2
– 1), A(- 2, ln 2),
B(3, ln 8). -
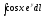 ,
Г: y
= ln cosx,
A(0, 0), B(
,
Г: y
= ln cosx,
A(0, 0), B(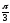 ,
-ln 2).
,
-ln 2). -
 ,
Г:
,
Г:
 ,
A(1,
,
A(1,
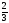 ),
B(3,
),
B(3,
 ).
). -
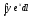 ,
Г: y
= ex,
A(0, 1), B(ln 2,
2).
,
Г: y
= ex,
A(0, 1), B(ln 2,
2). -
 ,
Г: y
= x3,
A(1, 1), B(2, 8).
,
Г: y
= x3,
A(1, 1), B(2, 8). -
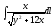 ,
Г: y
= 2x – 3,
A(0, -3), B(2, 1).
,
Г: y
= 2x – 3,
A(0, -3), B(2, 1). -
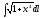 ,
Г: y
=
,
Г: y
= x3,
A(0, 0), B(3, 9).
x3,
A(0, 0), B(3, 9). -
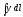 ,
Г: y2
= 4x,
A(0, 0), B(4, 4).
,
Г: y2
= 4x,
A(0, 0), B(4, 4). -
 ,
Г: y
= ln sinx,
A(1, 0), B(
,
Г: y
= ln sinx,
A(1, 0), B(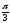 ,
,
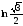 ).
). -
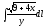 ,
Г: y2
= 9x,
A(1, 3), B(4, 6).
,
Г: y2
= 9x,
A(1, 3), B(4, 6). -
 ,
Г: y
= ln x,
A(1, 0), B(e4,
4).
,
Г: y
= ln x,
A(1, 0), B(e4,
4). -
 ,
Г: y
=
,
Г: y
=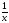 ,
A(1, 1), B(2,
,
A(1, 1), B(2,
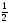 ).
). -
 ,
Г: y
= ex,
A(0, 1), B(4, e4).
,
Г: y
= ex,
A(0, 1), B(4, e4). -
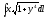 ,
Г: y
=
,
Г: y
= ,
A(1, 1), B(4,
,
A(1, 1), B(4,
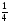 ).
). -
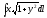 ,
Г: y =
e-x,
A(-3, e3),
B(0, 1).
,
Г: y =
e-x,
A(-3, e3),
B(0, 1). -
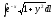 ,
Г: y =
ex,
A(0, 1), B(2, e4).
,
Г: y =
ex,
A(0, 1), B(2, e4). -
 ,
Г: y =
e-x,
A(-4, e4),
B(0, 1).
,
Г: y =
e-x,
A(-4, e4),
B(0, 1). -
 ,
Г: y
=
,
Г: y
=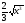 ,
A(0, 0), B(4,
,
A(0, 0), B(4,
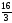 ).
). -
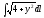 ,
Г: y
=
,
Г: y
=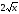 ,
A(1, 2), B(4, 4).
,
A(1, 2), B(4, 4). -
 ,
Г: y
= ln x,
A(1, 0), B(4, ln4).
,
Г: y
= ln x,
A(1, 0), B(4, ln4). -
 ,
Г: y
= ln x,
A(1, 0), B(4, ln4).
,
Г: y
= ln x,
A(1, 0), B(4, ln4). -
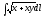 ,
Г:
,
Г:
 ,
A(1, 0), B(3, 4).
,
A(1, 0), B(3, 4). -
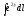 ,
Г: y
= ln x,
A(
,
Г: y
= ln x,
A( ,
ln
,
ln ),
B(
),
B(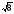 ,
ln
,
ln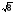 ).
). -
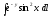 ,
Г: y
= ln cos
x, A(0,
0), B(
,
Г: y
= ln cos
x, A(0,
0), B(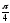 ,
,
 ).
). -
 ,
Г: y
= ln cos
x, A(0, 0), B(
,
Г: y
= ln cos
x, A(0, 0), B(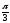 ,
,
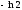 ).
). -
 ,
Г: y
= ln sin
x,
A(
,
Г: y
= ln sin
x,
A( ,
,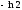 ),
B(
),
B(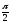 ,0).
,0). -
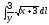 ,
Г: y
= ch x,
A(1, ch 1),
B(6, ch
6).
,
Г: y
= ch x,
A(1, ch 1),
B(6, ch
6). -
 ,
Г: y
= 3x –
2, A(1, 1), B(3, 7).
,
Г: y
= 3x –
2, A(1, 1), B(3, 7). -
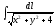 ,
Г: y
= 2x,
A(0, 0), B(1, 2).
,
Г: y
= 2x,
A(0, 0), B(1, 2). -
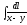 ,
Г: y
=
,
Г: y
=
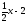 ,
A(0, -2), B(4, 0).
,
A(0, -2), B(4, 0).
-
Задание 2. Дуга Г задана параметрическими уравнениями, ρ – линейная плотность. Найти массу дуги.
-
x = t – sin t, y = 1 – cos t,
 ,
,
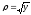 .
. -
x = 2 cos t, y = 2 sin t, z = 3t,
 ,
,
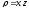 .
. -
 ,
,
 ,
,
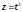 ,
,
 ,
,
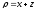 .
. -
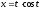 ,
,
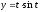 ,
,
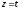 ,
,
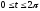 ,
,
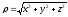 .
. -
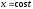 ,
,
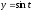 ,
,
 ,
,
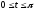 ,
,
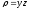 .
. -
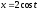 ,
,
 ,
,
 ,
,
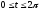 ,
,
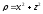 .
. -
 ,
,
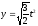 ,
,
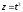 ,
,
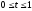 ,
,
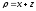 .
. -
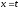 ,
,
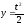 ,
,
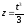 ,
,
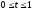 ,
,
 .
. -
 ,
,
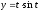 ,
,
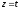 ,
,
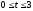 ,
,
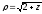 .
. -
 ,
,
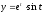 ,
,
 ,
,
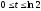 ,
,
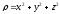 .
. -
 ,
,
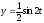 ,
,
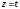 ,
,
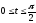 ,
,
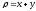 .
. -
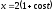 ,
,
 ,
,
 ,
,
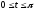 ,
,
 .
. -
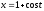 ,
,
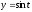 ,
,
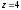 ,
,
 ,
,
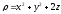 .
. -
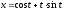 ,
,
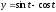 ,
,
 ,
,
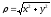 .
. -
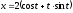 ,
,
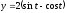 ,
,
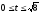 ,
,
 .
. -
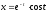 ,
,
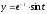 ,
,
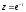 ,
,
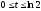 ,
,
 .
. -
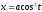 ,
,
 ,
,
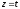 ,
,
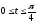 ,
,
 .
. -
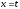 ,
,
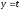 ,
,
 ,
,
 ,
,
 .
. -
 ,
,
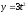 ,
,
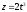 ,
,
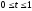 ,
,
 .
. -
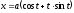 ,
,
 ,
,
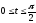 ,
,
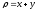 .
. -
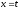 ,
,
 ,
,
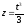 ,
,
 ,
,
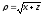 .
. -
 ,
,
 ,
,
 ,
,
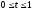 ,
,
 .
. -
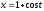 ,
,
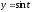 ,
,
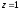 ,
,
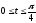 ,
,
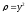 .
. -
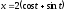 ,
,
 ,
,
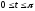 ,
,
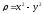 .
. -
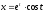 ,
,
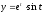 ,
,
 ,
,
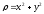 .
. -
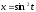 ,
,
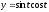 ,
,
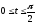 ,
,
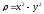 .
. -
 ,
,
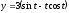 ,
,
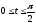 ,
,
 .
. -
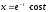 ,
,
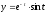 ,
,
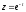 ,
,
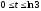 ,
,
 .
. -
 ,
,
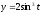 ,
,
 ,
,
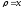 .
. -
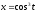 ,
,
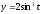 ,
,
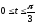 ,
,
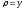 .
.
-
Задание 3. Вычислить криволинейный интеграл второго рода вдоль заданной линии L от точки А до точки В.
-
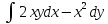 , L:
, L:
 , A(0,0), B(2,1).
, A(0,0), B(2,1). -
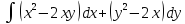 , L:
, L:
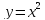 , A(-1,1), B(1,1).
, A(-1,1), B(1,1). -
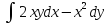 , L:
, L:
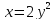 , A(0,0), B(2,1).
, A(0,0), B(2,1). -
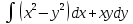 , L:
, L:
 , A(-1,1), B(3,4).
, A(-1,1), B(3,4). -
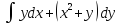 , L:
, L:
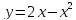 , A(-1,-3), B(1,1).
, A(-1,-3), B(1,1). -
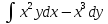 , L:
, L:
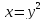 , A(1,1), B(4,2).
, A(1,1), B(4,2). -
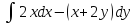 , L:
, L:
 , A(1,-3), B(3,-3).
, A(1,-3), B(3,-3). -
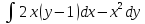 , L:
, L: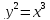 , A(1,1), B(4,8).
, A(1,1), B(4,8). -
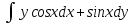 , L:
, L:
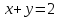 , A(2,0), B(0,2).
, A(2,0), B(0,2). -
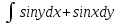 , L:
, L:
 , A(0,
, A(0, ), B(
), B(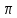 ,0).
,0). -
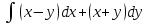 , L:
, L:
 , A(1,1), B(2,8).
, A(1,1), B(2,8). -
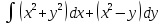 , L:
, L:
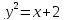 , A(2,2), B(7,3).
, A(2,2), B(7,3). -
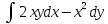 , L:
, L:
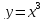 , A(0,0), B(1,1).
, A(0,0), B(1,1). -
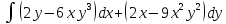 , L:
, L:
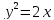 , A(0,0), B(2,2).
, A(0,0), B(2,2). -
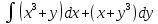 , L:
:
, L:
:
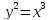 , A(0,0), B(1,1).
, A(0,0), B(1,1). -
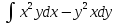 , L:
, L:
 , A(1,2), B(3,6).
, A(1,2), B(3,6). -
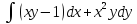 , L:
, L:
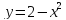 , A(0,2), B(1,1).
, A(0,2), B(1,1). -
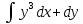 , L:
, L:
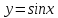 , A(0,0), B(
, A(0,0), B(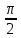 ,1).
,1). -
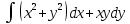 , L:
, L:
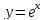 , A(0,1), B(1,e).
, A(0,1), B(1,e). -
 , L:
, L:
 , A(0,1), B(-1,e).
, A(0,1), B(-1,e). -
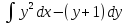 , L:
, L:
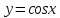 , A(0,1), B(
, A(0,1), B(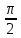 ,0).
,0). -
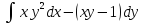 , L:
, L:
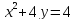 , A(0,1), B(2,0).
, A(0,1), B(2,0). -
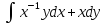 , L:
, L:
 , A(1,0), B(e,1).
, A(1,0), B(e,1). -
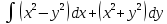 , L:
, L:
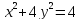 , A(2,0), B(0,1).
, A(2,0), B(0,1). -
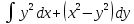 , L:
, L:
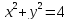 , A(0,2), B(2,0).
, A(0,2), B(2,0). -
 , L:
, L:
 , A(1,1), B(2,
, A(1,1), B(2, ).
). -
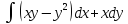 , L:
, L:
 , A(0,0), B(1,2).
, A(0,0), B(1,2). -
 , L:
, L:
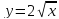 , A(0,0), B(1,2).
, A(0,0), B(1,2). -
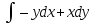 , L:
, L:
 , A(0,0), B(2,8).
, A(0,0), B(2,8). -
 , L:
, L:
 , A(1,0), B(0,-1).
, A(1,0), B(0,-1).
-
Задание 4. Вычислить криволинейный интеграл второго рода вдоль линии L, заданной параметрическими уравнениями.
-
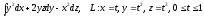 .
. -
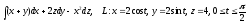
-
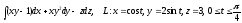 .
. -
 .
. -
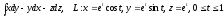 .
. -
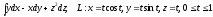 .
. -
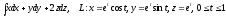 .
. -
 .
. -
 .
. -
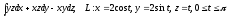 .
. -
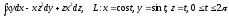 .
. -
 .
. -
 .
. -
 .
. -
 .
. -
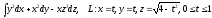 .
. -
 .
. -
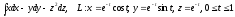 .
. -
 .
. -
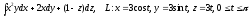 .
. -
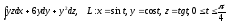 .
. -
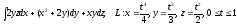 .
. -
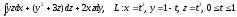 .
. -
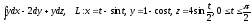 .
. -
 .
. -
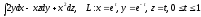 .
. -
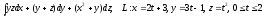 .
. -
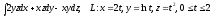 .
. -
 .
. -
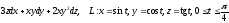 .
.
-
Задание 5. Вычислить криволинейный интеграл по замкнутому контуру, применяя формулу Грина.