
- •Глава II
- •2. Дискретные и непрерывные случайные величины
- •3. Законы распределения дискретной случайной
- •4. Функция распределения случайной величины, функция
- •5. Производящая функция дискретной случайной величины
- •6. Плотность распределения вероятностей
- •Тема 8. Числовые характеристики
- •1. Математическое ожидание случайной величины
- •2. Дисперсия случайной величины
- •3. Среднее квадратичное отклонение
- •4. Среднее квадратичное отклонение суммы
- •5. Одинаково распределённые взаимно
- •6. Мода и медиана, моменты случайных величин
- •7. Асимметрия и эксцесс, квантили
- •8. Производящая функция
- •Тема 9. Основные законы распределения
- •1. Биномиальный закон распределения (Закон Бернулли)
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределения
- •5. Равномерный закон распределения
- •2. .
- •6. Показательный закон распределения
- •7. Функция надёжности, показательный закон надёжности
- •8. Характеристическое свойство показательного
- •9. Нормальный закон распределения
- •Тема 10. Предельные теоремы теории вероятностей
- •1. Неравенство Чебышева и Маркова
- •2. Теорема Чебышева (збч Чебышева)
- •3. Ещё раз о теореме Бернулли
- •4. Центральная предельная теорема
- •0,04, Т.Е..
- •5. Применение цпт
- •6. Примеры на применение нормального закона
2. Дисперсия случайной величины
Этот пункт начнём с рассмотрения,
следующих примеров. Пусть д.с.в.
![]() ,
заданны следующими законами распределения:
,
заданны следующими законами распределения:
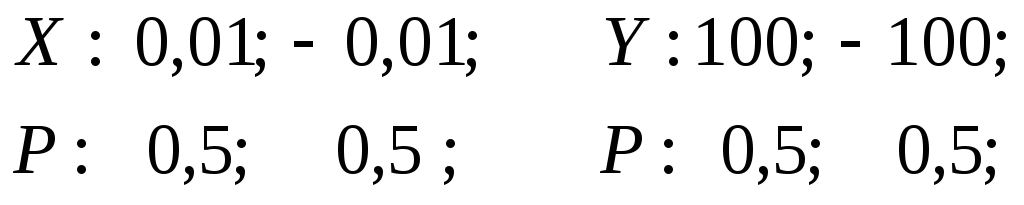
Найдём
математические ожидания случайных
величин
![]()
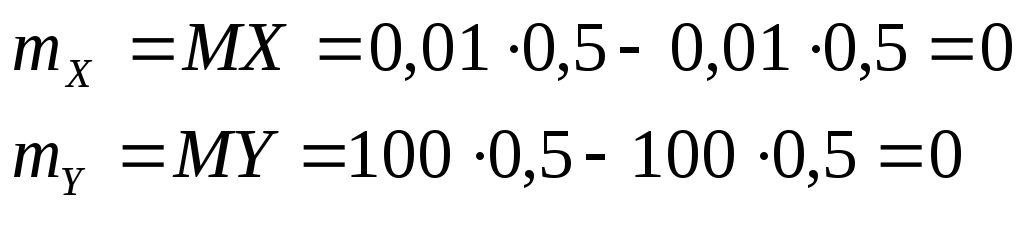
В этих примерах математическое ожидание
обеих случайных величин одинаковы, а
возможные их значения различны, причём
с.в.
![]() принимает относительно близкие значения
к м.о., а
принимает относительно близкие значения
к м.о., а![]() далёкие
значения от своего м.о.
далёкие
значения от своего м.о.
Следовательно, зная только математическое ожидание случайной величины, ещё нельзя судить ни о том, какие возможные значения она может принимать, тем более ни о том, как они распределены (рассеяны) в окрестности математического ожидания.
Это явление показывает, что математическое ожидание в общем случае случайную величину не может достаточно полно охарактеризовать.
По этой причине, наряду с понятием
математического ожидания в теории
вероятностей рассматривают и другие
числовые характеристики: дисперсия
(мера рассеяние с.в. от м.о. и понятие
среднее квадратичное отклонение).
Понятие дисперсия тесно связана с
понятием квадратичного отклонения
значения с.в. от своего м.о. В предыдущем
пункте мы отметили важное свойство
м.о.С.4.![]() Это равенство показывает, что одни
возможные отклонения положительны, а
другие – отрицательны: в результате
их взаимного погашения (происходит
«интерференция»)среднее значение
отклоненияокажется равным нулю.
Поэтому, целесообразно заменить эти
возможные отклонения их абсолютными
значениями или их квадратами.
Это равенство показывает, что одни
возможные отклонения положительны, а
другие – отрицательны: в результате
их взаимного погашения (происходит
«интерференция»)среднее значение
отклоненияокажется равным нулю.
Поэтому, целесообразно заменить эти
возможные отклонения их абсолютными
значениями или их квадратами.
Следует заметить, что на практике удобно
и в основном пользуются квадратом
отклонения, так как функция
квадратичного отклонения![]() является значительно «гладкой
функцией» по сравнению с функцией
абсолютного значения
является значительно «гладкой
функцией» по сравнению с функцией
абсолютного значения![]() .
.
Дисперсией (рассеянием) дискретной
с.в.![]() называется
математическое ожидание квадрата ее
отклонения от своего математического
ожидания.
называется
математическое ожидание квадрата ее
отклонения от своего математического
ожидания.
Это число обозначается
![]() или
или![]() ,
если ясно о чем идет речь. Таким образом,
по определению
,
если ясно о чем идет речь. Таким образом,
по определению
(10)
![]() или
или![]() .
или
.
или![]()
Из определения дисперсии следует, что
она характеризует разброс значений
с.в.
![]() относительно ее математического
ожидания, и имеет место следующие
равенства:
относительно ее математического
ожидания, и имеет место следующие
равенства:
(11)
![]() , если
, если![]() дискретная с.в.;
дискретная с.в.;
(12)
![]() если
если![]() непрерывная с.в..
непрерывная с.в..
На практике для нахождения дисперсии удобно пользоваться следующей формулой.
Теорема 8.1. Дисперсия равна
разности между математическим ожиданием
квадрата с.в.![]() и
квадратом ее математического
ожидания:
и
квадратом ее математического
ожидания:
(13)
![]() .
.
Доказательство. Математическое
ожидание с.в.![]() есть
постоянное число, следовательно,
величины
есть
постоянное число, следовательно,
величины![]() и
и![]() есть
также постоянные величины. На основании
свойства м.о. имеем
есть
также постоянные величины. На основании
свойства м.о. имеем
![]() .
.
Утверждение доказано.
Равенство (13) позволяет переписать равенства (11) и (12) в виде:
(14)
![]() ,
если
,
если![]() дискретная с.в.;
дискретная с.в.;
(15)
![]() ,если
,если![]() непрерывная с.в.
непрерывная с.в.
Очевидно, что ввиду
![]() непосредственно следуют справедливости
неравенства:
непосредственно следуют справедливости
неравенства:
![]()
![]() если с.в.
если с.в.![]() дискретна;
дискретна;
![]() если
с.в.
если
с.в.![]() непрерывна
непрерывна
Свойства дисперсии случайных величин.
С.1. Дисперсия постоянной величины равна нулю, т.е.
![]() .
.
С.2. Постоянный множитель выносится за знак дисперсии, возведя его в квадрат, т.е.
![]() .
.
С.3. Дисперсия суммы независимых с.в. равна сумме их дисперсий, т.е.
![]()
С.4. Дисперсия с.в. остается неизменным, если к этой с.в. прибавить постоянную величину, т.е. ( и с учётомС.2.) имеет место равенства
![]()
С.5. Если с.в.![]() -независимы,
то справедливо равенство
-независимы,
то справедливо равенство
![]() ,
,
Проверим свойства дисперсии.
1.
![]()
2.
![]()
Замечание. Следует отметить,
что при![]() случайная величина
случайная величина![]() имеет
возможные значения (по абсолютной
величине), большие, чем случайная
величина
имеет
возможные значения (по абсолютной
величине), большие, чем случайная
величина![]() .Отсюда
следует, что эти значения рассеяны
вокруг м.о.
.Отсюда
следует, что эти значения рассеяны
вокруг м.о.![]() больше, чем возможные значения
больше, чем возможные значения![]() вокруг
вокруг![]() ,
т.е.
,
т.е.![]() .
Напротив, если
.
Напротив, если![]() ,
то
,
то![]() .
.
3. На основании равенства (13) и свойства м.о. получим:
![]()
![]()
=![]() ,
,
Аналогично выводится и другая формула
![]()
![]()
потому,
что для независимыхс.в.![]() и
и![]() имеет
место равенство
имеет
место равенство![]()
С.4.выводится непосредственно изС.3.иС.1.СвойствоС.5. так же
является следствием равенства (13).
Достаточно использовать замену![]() ,
а затем воспользоваться свойствами
математического ожидания.
,
а затем воспользоваться свойствами
математического ожидания.
Заметим, что для нахождения значении
дисперсии удобно пользоваться для
д.с.в.
![]() равенством (14) и для н.с.в.
равенством (14) и для н.с.в.![]() равенством
(15).
равенством
(15).
