5. Производящая функция дискретной случайной величины

Кратко остановимся на понятие производящей функции конечных дискретных случайных величин.

Функцию определённую равенством , где некоторый параметр называют производящей функцией для последовательности повторных независимых опытов. Очевидно, что приимеет место равенство

,

для любого натурального числа

Пусть производится испытаний, причём в первом испытания вероятность появления событияравнаво втором равнавм испытании равнаи вероятностинепоявлениясобытиясоответственно равныЗаобозначим вероятность появления событиявиспытаниях ровнораз.

Производящей функцией вероятностей называют функцию, определяемую равенством

()

Таким образом, вероятность равна коэффициенту прий степени многочлена, определённой равенством (), т.е. равна коэффициенту прив разложении производящей функции по степеням.

Замечание. Отметим, что придолжно выполняться равенство (обычно называется контроль).

().

При имеем равенство

.

Следовательно, коэффициент при равно, приравнои при.

Следует заметить, что если в различных испытаниях появляется различные события (в первом испытании событие , во втором событиеи т.д.), то изменяется лишь истолкование коэффициентов при различных степенях. Например, в равенстве () коэффициентопределяет вероятность появления двух событийи.

Пример 8. Устройство состоит из трёх независимо работающих элементов. Вероятности безотказной работы элементов (за время) соответственно равныНайти вероятности того, что за времябудут работать безотказно:

а) все три элемента работают;

б) два элемента работают;

в) один элемент работает;

г) ни один из элементов не будет работать.

Решение. Вероятности безотказной работы элементов соответственно равныСледовательно, вероятности того, что элементы откажут, соответственно равны

Составим производящую функцию:

а) Вероятность того, что три элемента будут работать безотказно, равна коэффициенту при

б) Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при

в) Вероятность того, что один элемент будет работать безотказно, равна коэффициенту при

г) Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену:

Легко видет, что выполняется контроль:

.

Задания. Покажите, что

1. гдештрихозначаетю производную функциипо параметрупричём

2.

3.,

гдечисло размещений изэлементов по.

Заметим, что вероятности ,являются коэффициентами при степенив разложении

.

6. Плотность распределения вероятностей

непрерывной случайной величины

Важнейшей характеристикой непрерывной случайной величины (кроме функции распределения) является так называемая функция плотности распределения.Напомним, что «Случайную величину называют непрерывной, если ее функция распределениянепрерывна в любой точке и дифференцируема всюду, за исключением, может быть отдельных точек».

Плотностью распределения вероятностейнепрерывнойслучайной величины называют некоторую функциюпервую производную от функции распределения:

(7) .

Из этого определения следует, что функция распределения является первообразной функциейдля функции плотности распределения.

Функцию называют такжедифференциальной функцией распределения: она выражает одной из форм закона распределения случайной величины, относящихся только к непрерывным случайным величинам.

Следует заметить, что для описания распределения вероятностей д.с.в. понятие плотность распределения неприменима.

Рассмотрим вероятностный смысл плотности распределения. По определению производной функции имеем

Далее, согласно формуле (2), выполняется равенство

Отношение представляет собой «среднюю вероятность», которая приходится на единицу длины участка. Тогда получим

(8) ,

т.е. плотность распределения н.с.в. равна пределу отношения вероятности попадания н.с.в.в промежутокк длинеэтого промежутка, когда величинастремиться к нулю. Из равенства (8) следует, что.

Тем самым, установлено, что плотность вероятности н.с.в. определяется как функцияудовлетворяющая, условию. Выражениеназываетсяэлементом вероятности.

Следует отметить, что понятие функции плотности распределения вероятности , аналогично таким понятиям, как плотность распределения масс на оси абсцисс или плотность распределения электрического тока в теории электричества в физике и т.д.

Теперь, рассмотрим свойства функции плотности распределения.

С.1. .- неотрицательная функция на всей числовой оси.

С.2. Вероятность попадания н.с.в. в промежутокравна определенному интегралу от ее функции плотности в пределах отдо, т.е. верно равенство

(9)

С.3. Если функция распределения н.с.в.и- функция плотности, то имеет место равенство

(10) .

С.4. Интеграл от функции плотности вероятности н.с.в. в бесконечных пределах равен единице (условие нормировки - контроль) т.е. еслиплотность распределения некоторой с.в., тогда

. (11).

Условие нормировки для н.с.в. напоминает аналога условия «контроля» для случая д.с.в..

1.Функция плотности распределения- неотрицательная функция потому, что по определениюнеубывающая и монотонна, а следовательно. Это означает, что график функция плотности, называемыйкривой распределения, расположена не ниже оси абсцисс, также следует отметить, что функция плотности может принимать сколь угодно большие значения.

2.Посколькуестьпервообразнаяфункцией для функции, тогда в соответствии с формулой Ньютона-Лейбница справедливо равенство

(12)

Отсюда, согласно определению функции получим

(13) .

Геометрический смысл этого равенства следующее: интеграл от элемента вероятностиесть площадь фигуры (), ограниченной сверху кривой распределенияи опирающейся на отрезок [a;b]

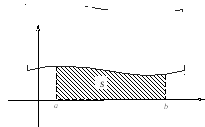
рис.21-Письменный

3.На основании свойстваС.2. И то, чтополучим:

(14) .

4.Подставляя в формуле (13) соответственно, получаем достоверное событиет.е.

(15) .

Геометрическая трактовка свойство С.4.(свойство нормировки) означает, что площадь фигуры (S) ограниченной функциейи числовой осью абсцисс, равна единице.

Теперь, мы можем дать определение непрерывной с.в. в связи с функцией распределения плотности :случайная величина называетсянепрерывной, если существует неотрицательная функция такая, что при любом её функция распределения можно представить в виде

;

отсюда получим равенство -дифференциальное равенство (дифференциальный закон распределения).

Следовательно, функций иявляются равноправными (эквивалентными) характеристиками случайной величины. Отметим, что на основании формулы (13) непосредственно следует равенство

.

Отсюда, также следуют равенства:

.

Пример 9. Пусть плотность распределения с.в.задана функцией,.

1. Найти значение параметра , при которомбудет функцией плотности,

2. Выписать функцию распределения .

Решение. На основанииС.4. должно выполняться равенство (см.(11))

.

Применяя метод подсчёта несобственных интегралов, при этом воспользуюсь табличным интегралом для функции арктангенса с последующим применением формулы Ньютона –Лейбница получим

.

Следовательно, . Далее, выпишем функцию распределения с.в.плотность распределения которой равна. Проведя обычные рассуждения на основании формулы (14) получим

.

Такое распределение называют распределением Коши.

Задание. Проверьте справедливость дифференциального закона распределения и убедитесь, чтоявляется первообразной функцией.

Пример 9. Пусть плотность распределения с.в.задана функцией,

1. Найти значение параметра , при которомбудет функцией плотности,

2. Выписать функцию распределения .

Решение. Аналогично как в примере 1 пользуясь равенством (11) получим

Следовательно,

Задание. 1. Проверьте справедливость дифференциального закона распределения и убедитесь, что является первообразной функцией для.

2. Пусть и плотность распределения н.с.в.задана функцией

Найти значение параметра C, выписать явный вид функции распределения и проверить выполнение дифференциального закона.

Пример 10. Однородная проволока длиной 1 м. растягивается за концы и при этом разрывается. Пустьслучайная величина, равная расстоянию от точки разрыва до левого конца проволки. Используя геометрические вероятности, найдём, что

для любых Следовательно, функция распределения и плотность распределения этой случайной величины имеют вид:

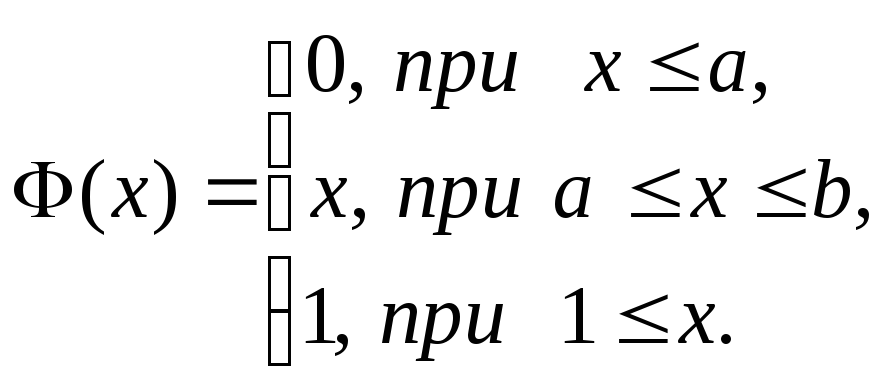
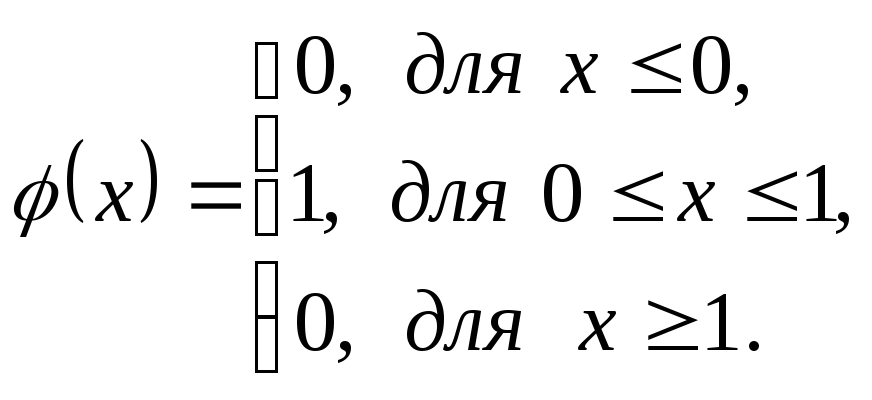
Задание. Проверьте выполнения дифференциального закона.