9. Нормальный закон распределения

Нормальный закон («закон Гаусса») играет исключительную роль в теории вероятностей и её приложениях. Главная особенность закона Гаусса состоит в том, он является предельным законом, к которому приближаются, при определённых условиях, другие законы распределения. Нормальный закон распределения наиболее часто встречается на практике и как правило, даёт необходимые результаты для приложения.

Говорят, что непрерывная с.в. распределена по нормальному закону с параметрамии , если её функция плотности распределения задаётся равенством

(29) .

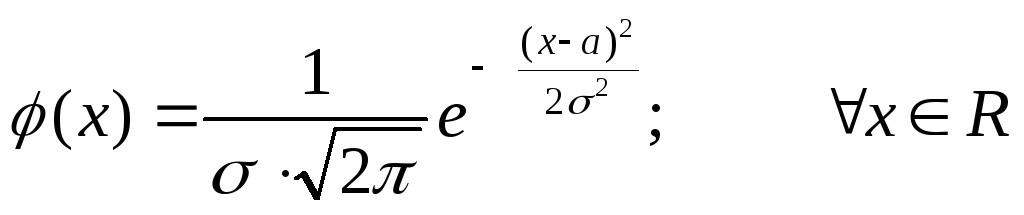В дальнейшем, тот факт, что н. с. в. имеет нормальное (или Гауссово) распределение с параметрамии, сокращенно обозначим: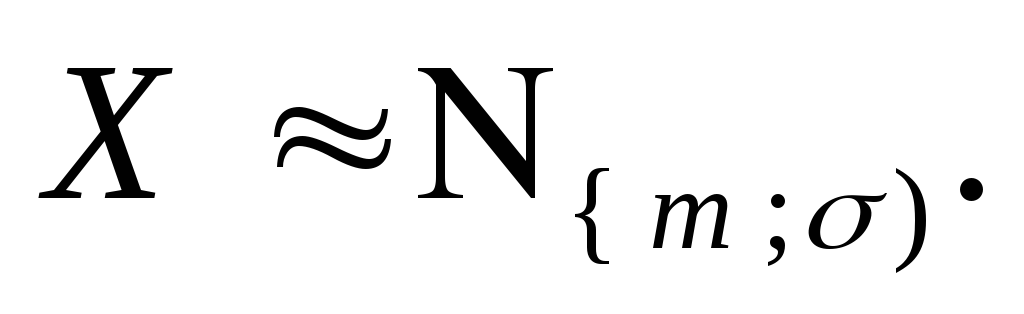Поэтому, чтобы задать нормальное распределение, достаточно задать эти два параметра.

Убедимся, что удовлетворяет условиям «быть функцией плотности».

Неравенство , непосредственно следует из определения (29).Проверим выполнение условия нормировки . Имеем (с учётом (29)) и элементарных преобразований и с последующим применением подстановкии известного равенства

(30) (интеграл Пуассона),

получим

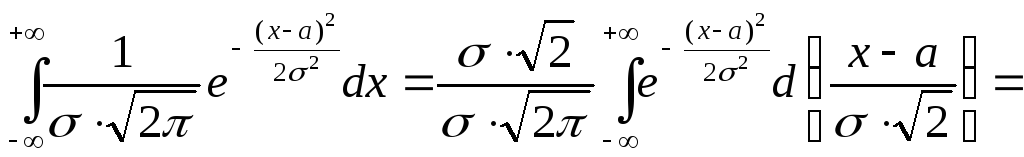
Условие нормировки выполняется. Следовательно, функция является функцией плотности.

Из равенства (30) (в силу чётности подынтегральной функции) следуют равенства:

(31) ;

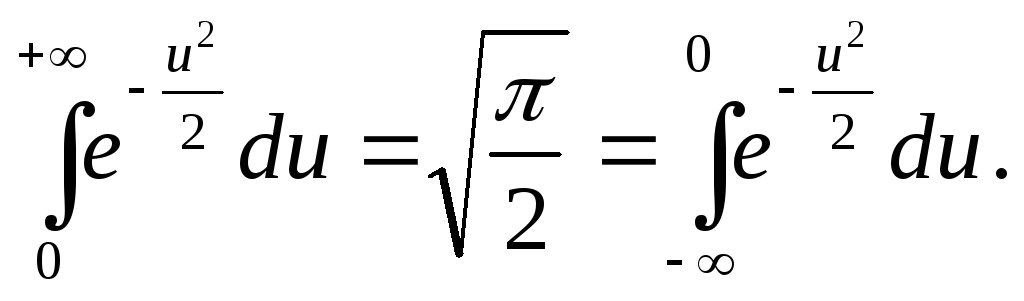
Функция распределения с.в.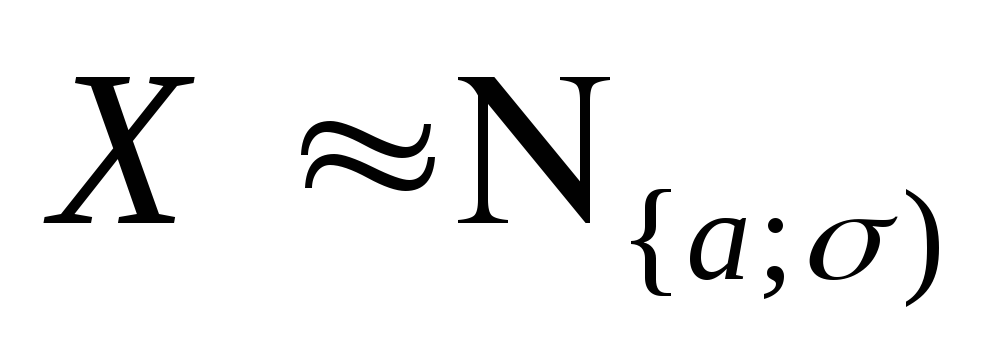определяется равенством:

(32) (Функция распределения)

Кратко ( Ф.Р).

С учётом (29) будем иметь

(33) .

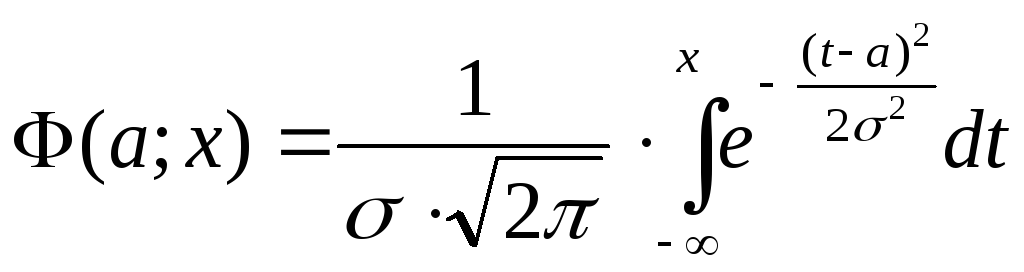В равенствах (29) и (33) полагая и, для нормального распределения с.в.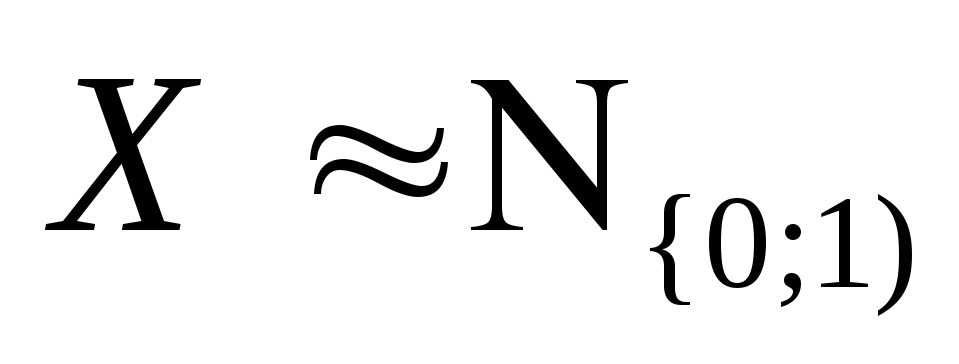(с учётом (29)) получим

(34)

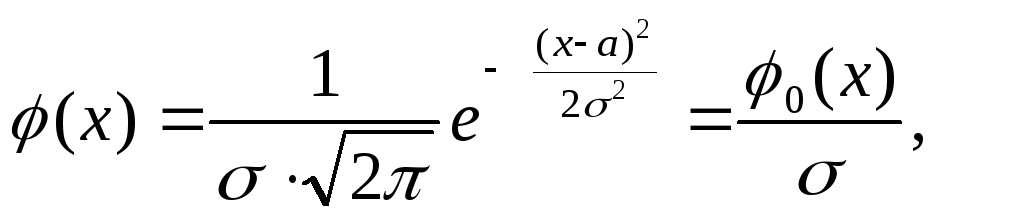
(35)

(36) (И.В. или Ф.Л);

Равенство (36) называется «интегралом вероятности» или Функция Лапласа(см. п.5-7., Т. 6).

Нормальное распределение с такими параметрами называются «нормированными или стандартными» распределениями. Мы уже встречались с этими функциями, (см. п п.5, 6, 7; Тема.6.). Кроме того, нами было отмечено, что т.е. функция Лапласа, (т.е. «интеграл вероятности») и нормированная функция Лапласа (Н.Ф.Л)

(36)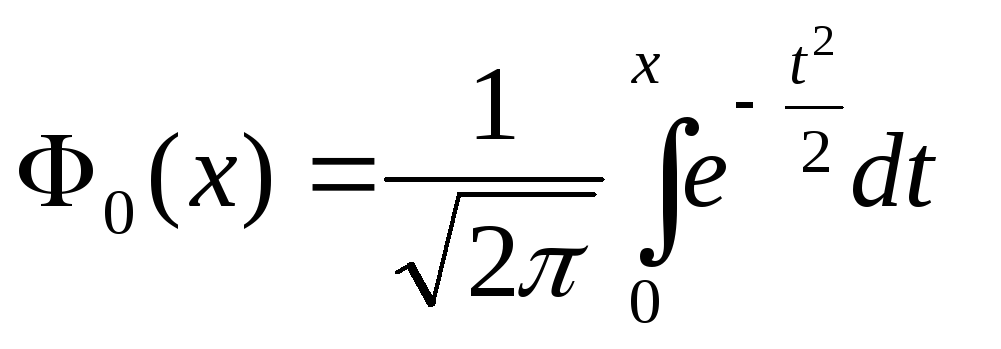(Н.Ф.Л.);

удовлетворяют равенству

(37)

Действительно, по формуле (36) имеем

Далее, на основании второго равенства (31) () первое слагаемое равно 0,5, а второе слагаемое равноРавенство (37) получено.Поэтому в приложениях достаточно знать значения функции , а эта функция табулирована (см. приложение…). Для нахождения значений функции Лапласа пользуются и друг0й формулой

которая является прямым следствием равенства (37).

Найдём вероятности попадания с.в. 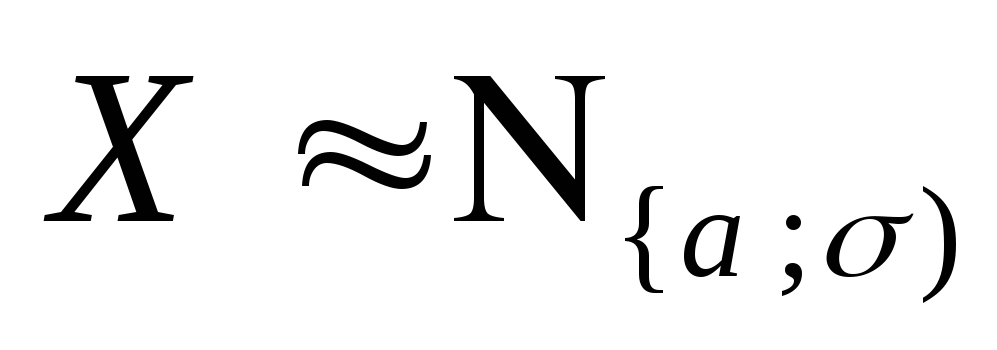на заданной участок отрезки числовой осиКак ранее было показано, вероятность значений н.с.в.распределённой на отрезкечисловой осис плотностью имеет вид

.

В случае нормального распределения с.в. 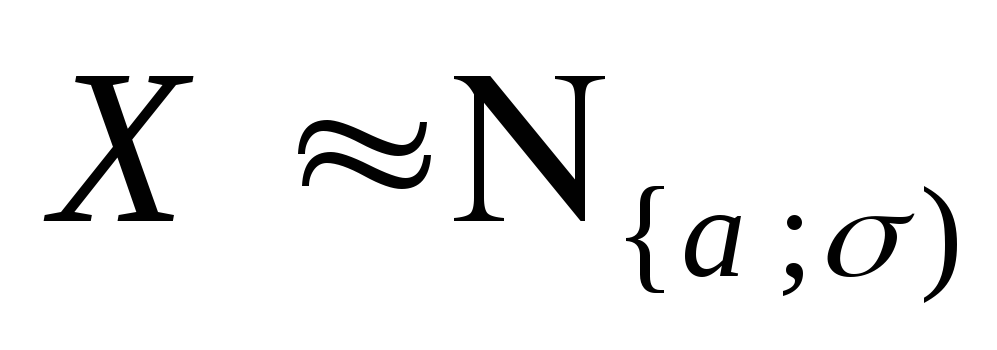, с учётом (37) имеем

=.

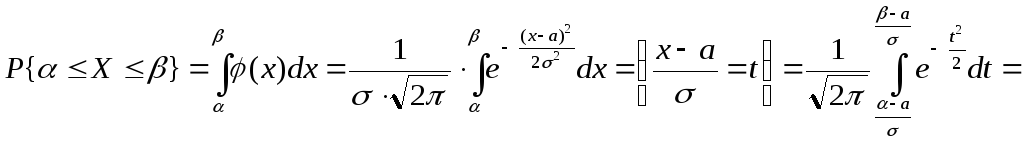
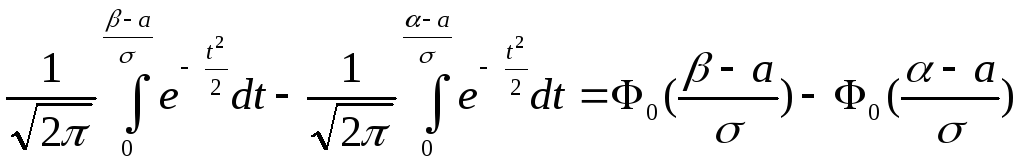Следовательно,

(38) .

Через функцию Лапласа выражается и функция распределенияс.в., т.е. через нормально распределённой случайной величины с.в..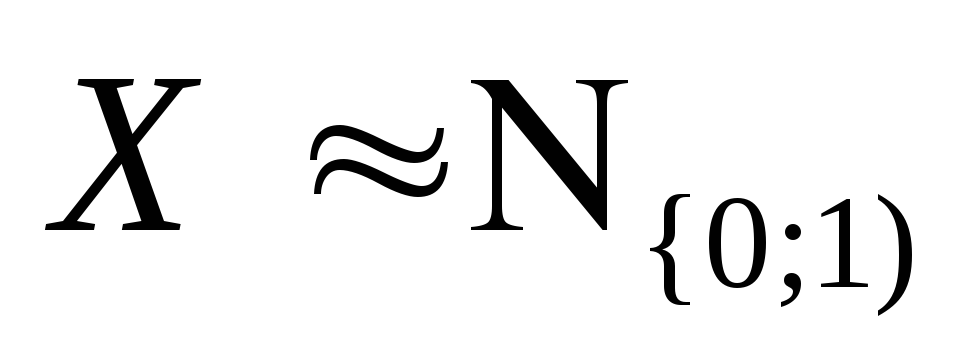

Теорема 9. 8. Для - функции распределения с.в.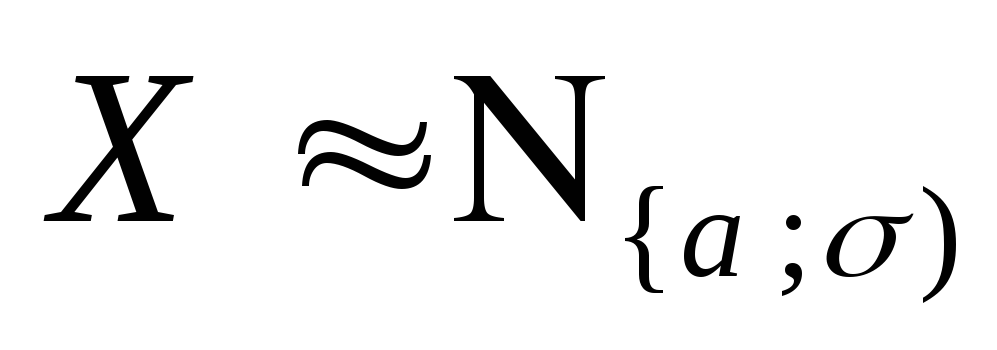справедливо равенство

(39) (вычислительная формула).

Доказательство. По формуле (33) , определению вероятности и с учётом равенство (38) имеем

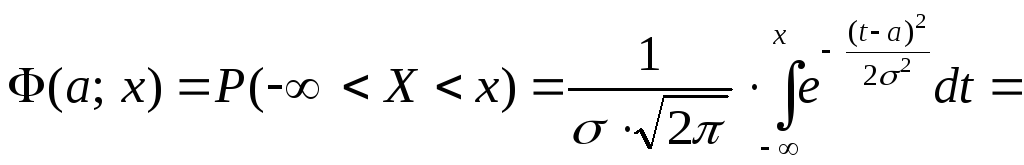
Далее, в силу нечётности функции и то, чтои второго равенства

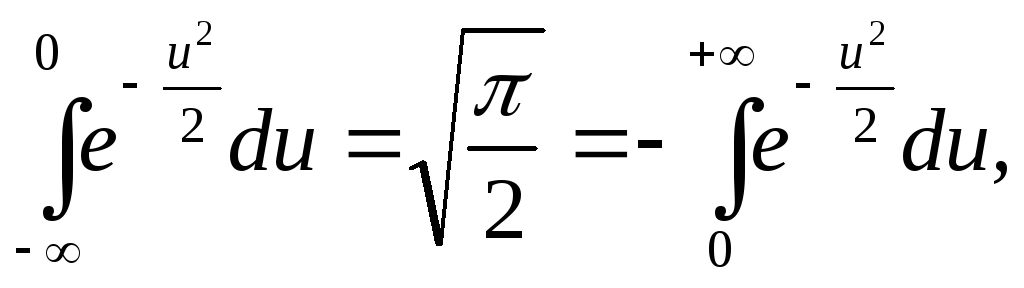
из формулы (31) получим, что , действительно

Теорема доказана.

Следствие. Для -функции распределения с.в.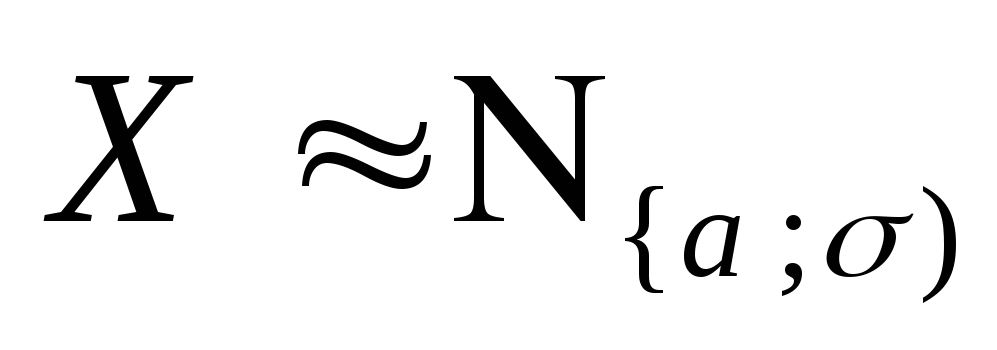,справедливы равенства:

(40)(Ф.Л.).

(41).

Действительно, по определению функции распределения (после замены и сучётом того, что величиныификсированные числа), имеем

.

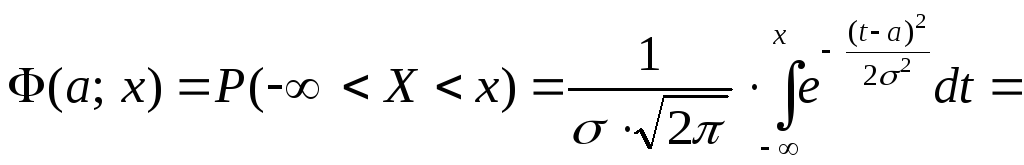
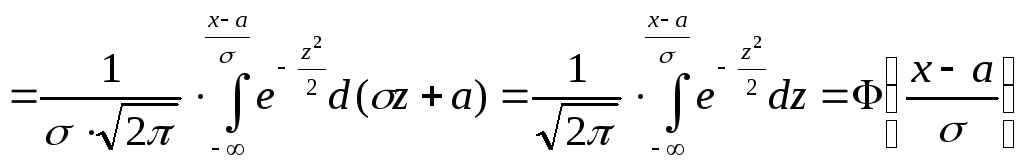Равенство (41) прямо следует из (38) путём прибавления к правой части этого равенства число с последующим использованием (37).

Теорема 9.9. Для вычисления математического ожидания и дисперсии нормального распределения с.в. 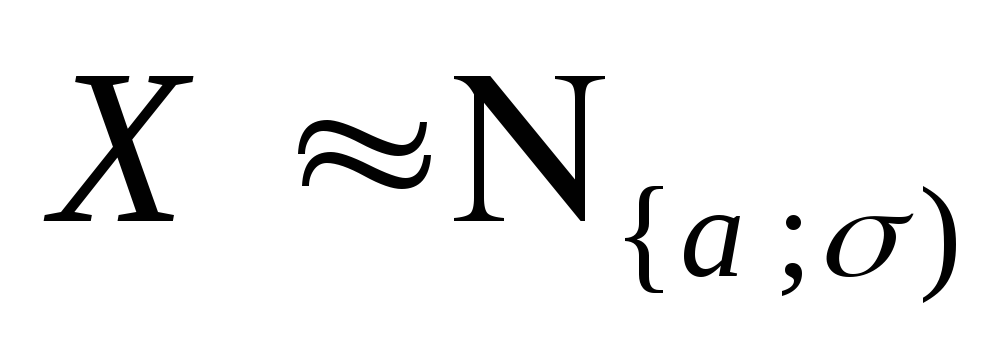, справедливы равенства:

(42)

Доказательство. По определению м.о. с.в. 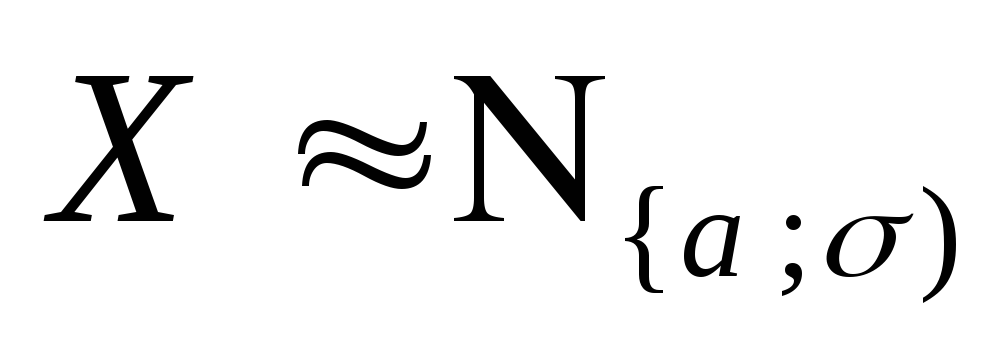,имеем

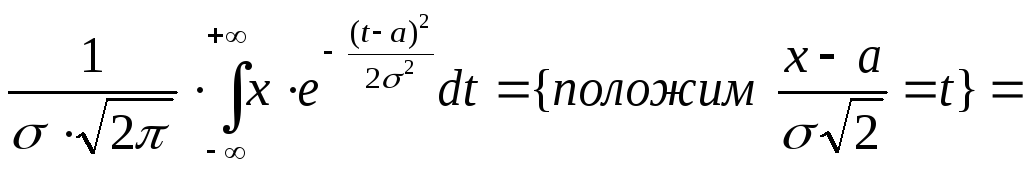
Первый интеграл равен нулю, так как подынтегральная функция нечетная, а пределы интегрирования симметричны относительно нуля, а второй интеграл согласно равенству (30) равен , следовательно, правая часть равна параметруматематическому ожиданию. Тем самым первая формула (42) получена.

Вычислим дисперсию с.в. 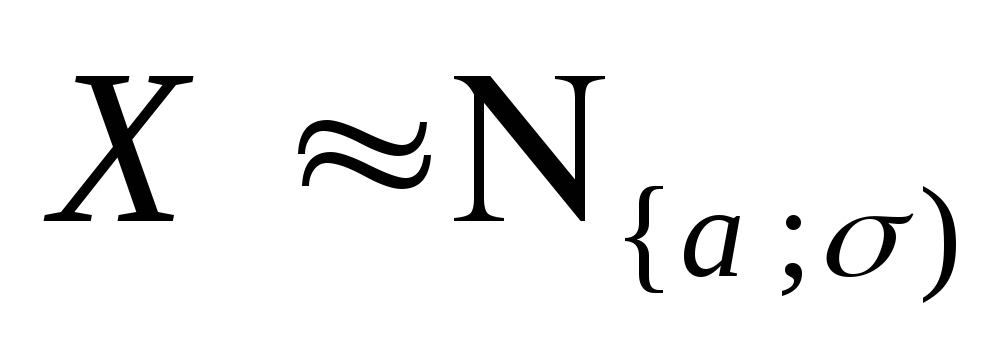.Снова сделаем подстановкуи применим метод интегрирования по частям с последующим применением формулы Пуассона (30), тогда получим: по определению дисперсии с.в. ,

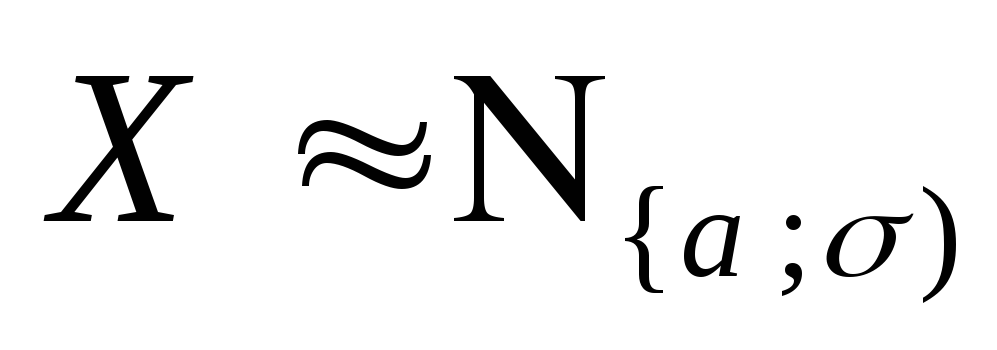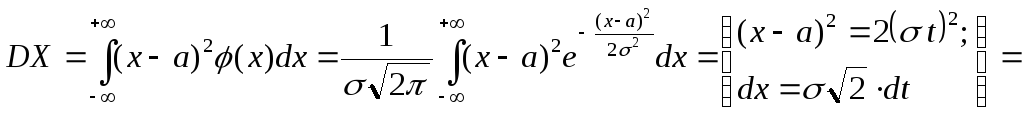
Таким образом, среднее квадратичное отклонение (илистандарт).

Теорема 9 полностью доказана.

Упражнения. Покажите, что для с.в. 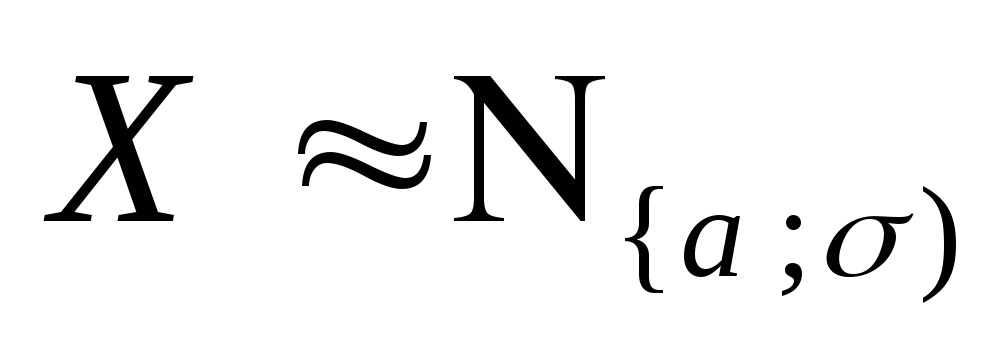выполняются следующие равенства:

1., где- точка максимума функции плотности.

2. . где- медиана с.в. 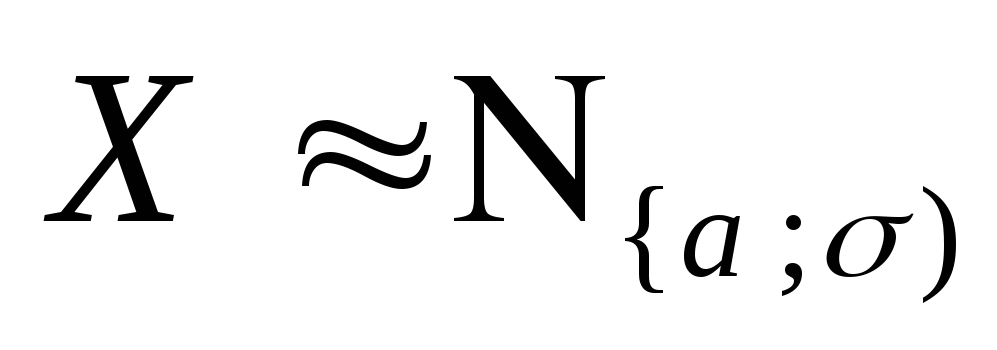(см.Т.8., п.6 равенство (23)).

3. коэффициент асимметрии 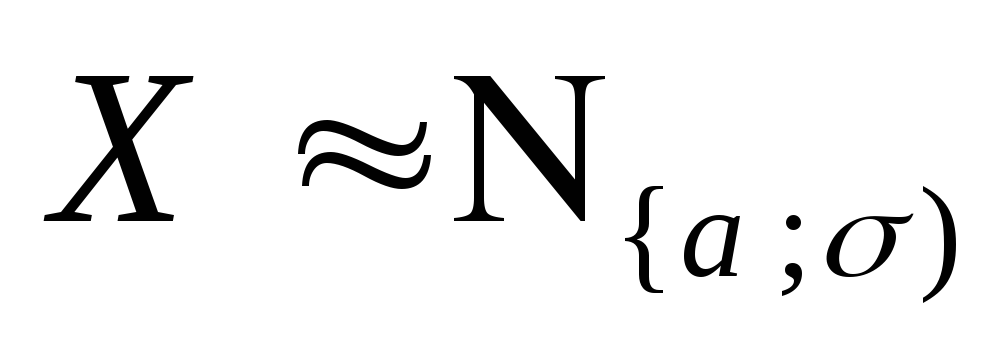(см. п.7., Т.8).

Это означает, что ассиметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; ассиметрия отрицательна, если «длинная часть» крывой распределения расположена слева от математического ожидания.

Практически знак асимметрии определяют по расположению кривой распределения относительно моды (точки максимума плотности распределения): если «длинная часть» кривой распределения расположена правее моды, то асимметрия положительна (рис.10, а), если левее моды, то асимметрия отрицательна (рис.10,б).

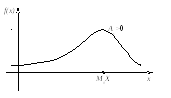
Рис. 10, из Гмурмана. Стр. 170)

4. коэффициент эксцесса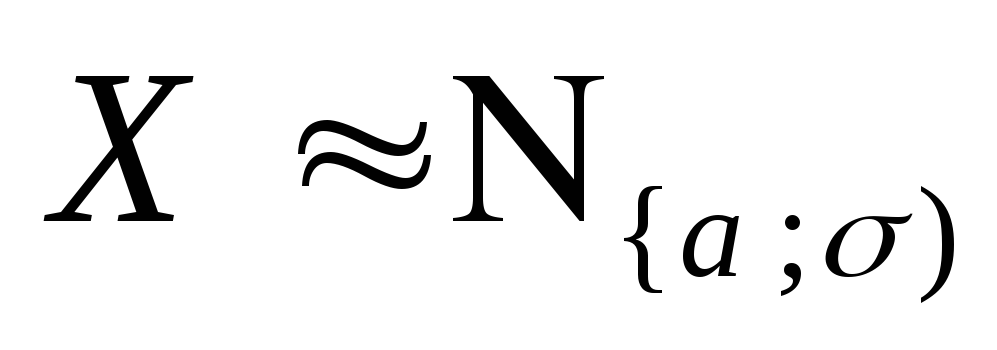(см. п.7.,Т.8).

Для нормального распределения , следовательно, эксцессПоэтому, если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой; если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая (рис.11,а); если эксцесс отрицательный, то сраниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая (рис.11,б). При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

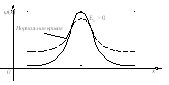
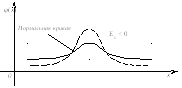
Рис. 11 из Гм. Стр. 171)

Исследование свойства функции Гаусса .

1.Как уже было отмечено ранее, для всех; график функции расположен выше оси

2.Осьслужит асимптотой графика функции ,так как

3. Функция имеет один единственный максимум в точкеравный

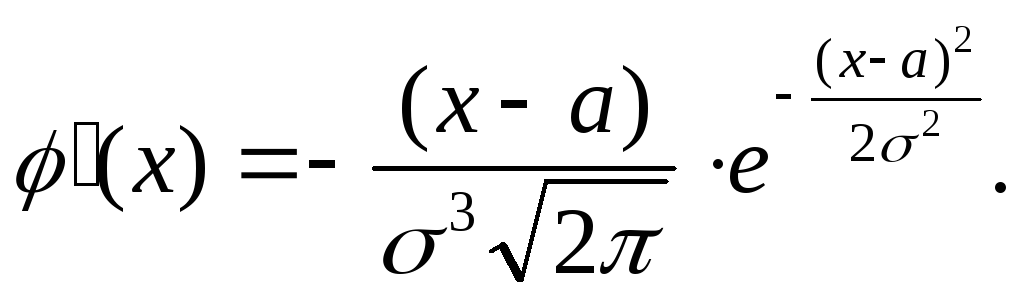. Действительно,Следовательно.припри этом: еслитоа еслитоЭто и означает, что точкаявляется точкой максимума нашей функции, т.е.

4.График функции симметричен относительно прямой , так как

аналитический вид функции содержит разностьв квадрате.

5. Можно убедиться, что иявляютсяточками перегиба графика функции .Действительно, найдём вторую производную функции нормального распределения с.в. .

.

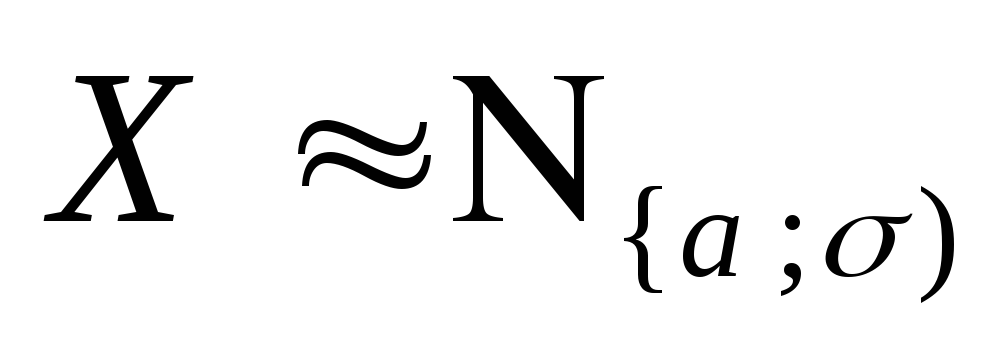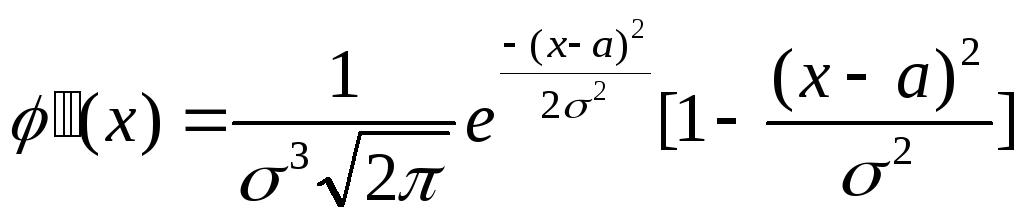Легко заметить, что a при переходе через эти точки она меняет знак (в обеих этих точках значение функции равна .

Таким образом, точки и являются точками перегиба графика функции .

На основании вышеуказанных свойств график функции Гаусса (или нормальной кривой) имеет вид:

Рис.34.из кн. Письменного

Рассмотрим, как изменяется график функции (кривая Гаусса) при изменении параметров ? При измененииграфик функции сохраняет свою форму, т.е. графики функции и

имеют одинаковую форму; одна из них от другого получается путём переноса «центра» на величину(еслив право, если же, то влево).

С изменением максимальная ордината точки кривой изменяется. Поскольку площадь, ограниченная кривой распределения, и осьюравна единице при любом значении, тогда

с возрастанием кривая Гаусса становится более «пологой», т.е. сжимается равномерно к оси а при убываниинормальная кривая становится более «островершинной» и растягивается в положительном направлении оси .

Рис.35. из Письм (или рис.8 из кн.Гмурман)

На рис. 35 изображены нормальные кривые при различных значениях и некотором значении параметра(одинаковом для всех трёх кривых).

Вычисление вероятности попадания с.в. 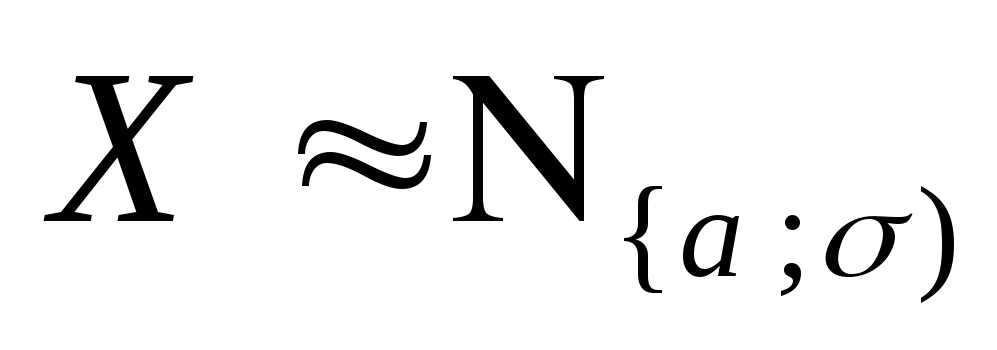в интервал.

Часто требуется вычислять вероятность попадания нормально распределенной случайной величины в интервал, симметричной, относительно центра рассеяния : Пусть для любого положительного числа, этим интервалом будетдлины, Другими словами, с.в.удовлетворяет двойному неравенству:

Тогда по формуле (38) с учётом нечётности функции распределения имеем

Следовательно,

(43) .

На рис.9 наглядно показано, что если две случайные величины нормально распределены и то вероятность принятия значение из интервалабольше у той величины, у которой меньше значение с. к. о.Этот факт полностью соответствует вероятному смыслу параметра,которая характеризует рассеяние с.в. вокруг ее математического ожидания.

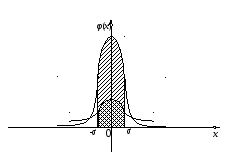
Рис. 9. из кн. Гм. Стр.166.

Пример 1. Пусть случайная величина распределена по нормальному закону 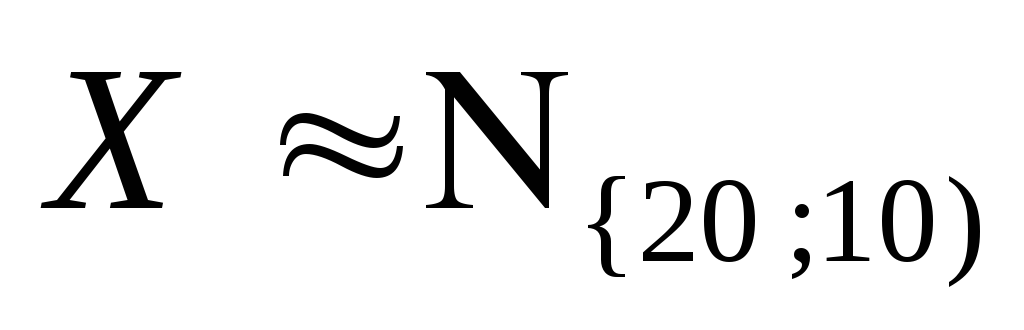с параметрамиНайти вероятность того, что отклонение по абсолютной величине будет меньше трёх.

Решение. На основании формулы (43) получим.

По таблице (приложение …) находим, следовательно,

Пример 2. При измерении детали получаются случайные ошибки, подчинённые нормальному закону с параметром10мм. Производится три независимых измерения детали. Найти вероятность того, что что ошибка хотя бы одного измерения не превосходит по модулю 2мм.

Решение. По формуле (43) находим:

Вероятность того, что эта ошибка (погрешность) превышает 2мм в одном опыте (измерении), равна

По теореме умножения вероятность тог, что во всех трёх опытах ошибка измерения превышает 2мм, равна

Следовательно, искомая вероятность равна 1-

Правило «сигм».Положим в равенстве (43), получим

(44) .

Если внимательно посмотреть на таблицу значений функции то мы увидем, что по мере роста величинызначении функции Лапласа фактически мало отличается от величины 0,5. По этой причине во многих практических задачах ограничиваются «правилом трёх сигм», т.е. мы приходим к очень важному утверждению:

Теорема 9.10.Практически достоверно, что с.в. 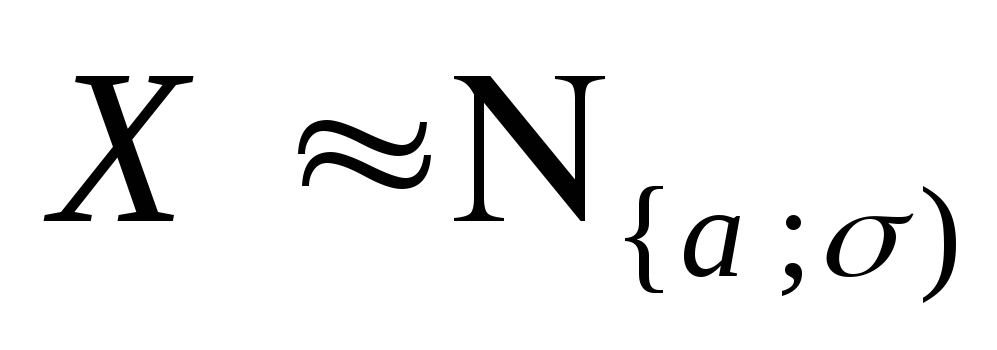принимает свои значения в промежуткеИменно из равенство(44)в указанном интервале имеет место

(45)

Другими словами: если с.в.распределена по нормальному закону, то абсолютная величина её отклонение от математического ожидания не превосходит от утроенного среднего квадратичного отклонения.

Задание. Убедитесь самостоятельно (на основании равенства (44) и таблицы значения функции Лапласа) в нижеследующих вычислительных формулах:

1. .

2.

3.

4,

На практике «правило трёх сигм» применяется следующим образом: если распределение, изучаемой величины неизвестно, но условие, указанное в приведённом правиле выполняется, тогда есть основание предположить, что изучаемая с.в. распределена по нормальному закону; в противном случае она распределена не по нормальному закону.

Нормальному закону подчиняются ошибки измерений, величина износа деталей в различных механизмах, рост человека, ошибки стрельбы, величина шума, в радиоприёмном устройстве, колебания курса акции в финансовых сферах и т.д.