
- •Глава II
- •2. Дискретные и непрерывные случайные величины
- •3. Законы распределения дискретной случайной
- •4. Функция распределения случайной величины, функция
- •5. Производящая функция дискретной случайной величины
- •6. Плотность распределения вероятностей
- •Тема 8. Числовые характеристики
- •1. Математическое ожидание случайной величины
- •2. Дисперсия случайной величины
- •3. Среднее квадратичное отклонение
- •4. Среднее квадратичное отклонение суммы
- •5. Одинаково распределённые взаимно
- •6. Мода и медиана, моменты случайных величин
- •7. Асимметрия и эксцесс, квантили
- •8. Производящая функция
- •Тема 9. Основные законы распределения
- •1. Биномиальный закон распределения (Закон Бернулли)
- •2. Распределение Пуассона
- •3. Геометрическое распределение
- •4. Гипергеометрическое распределения
- •5. Равномерный закон распределения
- •2. .
- •6. Показательный закон распределения
- •7. Функция надёжности, показательный закон надёжности
- •8. Характеристическое свойство показательного
- •9. Нормальный закон распределения
- •Тема 10. Предельные теоремы теории вероятностей
- •1. Неравенство Чебышева и Маркова
- •2. Теорема Чебышева (збч Чебышева)
- •3. Ещё раз о теореме Бернулли
- •4. Центральная предельная теорема
- •0,04, Т.Е..
- •5. Применение цпт
- •6. Примеры на применение нормального закона
Тема 9. Основные законы распределения
случайных величин
Среди общих законов д.с.в.
![]() наиболее
распространённым является биномиальный
закон распределения, с которым мы уже
встречались. Здесь рассмотрим более
подробно этот и другие законы, их
производящие функции и основные числовые
характеристики: м.о., дисперсия и среднее
квадратическое отклонение.
наиболее
распространённым является биномиальный
закон распределения, с которым мы уже
встречались. Здесь рассмотрим более
подробно этот и другие законы, их
производящие функции и основные числовые
характеристики: м.о., дисперсия и среднее
квадратическое отклонение.
1. Биномиальный закон распределения (Закон Бернулли)
Напомним, что если вероятность наступления
случайного события
![]() в каждом испытании равна
в каждом испытании равна![]() ,
,![]() .
Как было показано в первой части, при
этих условиях вероятность того, что
при
.
Как было показано в первой части, при
этих условиях вероятность того, что
при![]() испытаниях событие
испытаниях событие![]() осуществится
осуществится![]() раз, определяется формулой Бернулли
раз, определяется формулой Бернулли
![]() ..
..
или
![]()
где
![]() .Составим таблицу распределения
биномиального закона:
.Составим таблицу распределения
биномиального закона:
|
Х |
|
|
|
m |
|
|
|
P |
|
|
|
|
|
|
Контроль-![]()
Как было показано ранее из
![]() ,
ввиду равенства
,
ввиду равенства![]() получим
получим
![]() .
.
Биноминальнымназывается распределение
вероятностей, определяемое формулой
Бернулли. Закон называется «биноминальным»
потому, что правую часть равенства
![]() ,
можно рассматривать как общий член
разложения бинома Ньютона:
,
можно рассматривать как общий член
разложения бинома Ньютона:
![]() .
.
Таким образом, первый член разложения
![]() определяет вероятность наступления
рассматриваемого событияA
определяет вероятность наступления
рассматриваемого событияA
![]() раз вn– независимых
испытаниях; второй член
раз вn– независимых
испытаниях; второй член
![]() определяет вероятность наступления
события
определяет вероятность наступления
события![]() (
(![]() )
раз, и т.д. последний член
)
раз, и т.д. последний член![]() определяет вероятность того, что события
определяет вероятность того, что события![]() не появится ни разу.
не появится ни разу.
Функция распределения с.в.![]() распределенный по биномиальному закону,
имеет вил:
распределенный по биномиальному закону,
имеет вил:
(1)
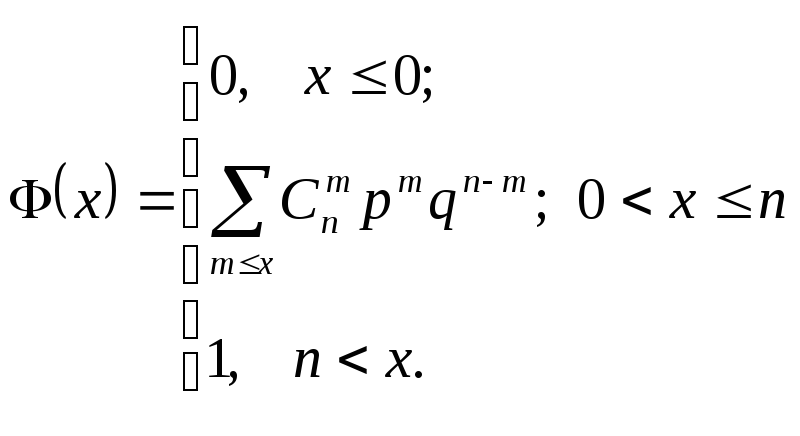
Выпишем производящую функцию биномиального распределения
(2)
![]()
То ест
![]() .
Очевидно,
.
Очевидно,
![]()
Продифферецируя
равенство (2) почленно относительно
![]() ,
получим соответственно
,
получим соответственно
(3)
![]()
Следовательно, имеет место утверждение
Теорема 9.1. Для числовых характеристик биномиального распределения имеют место равенства:
(4)
![]()
Доказательство. На основании
равенств (38) пункта 8 и равенства (3)
настоящего раздела, также с учётом
равенства![]() ,
получим
,
получим
![]()
![]()
Утверждение доказано.
Пример 1.Монета брошена 3 раза. Найти
закон распределения с.в.![]() -
числа выпадения герба, математическое
ожидание, дисперсию и среднее
квадратическое отклонение.
-
числа выпадения герба, математическое
ожидание, дисперсию и среднее
квадратическое отклонение.
Решение.Сначала найдем закон
распределения дискретной случайной
величины![]() ,
т.е.
,
т.е.![]() .
.
Вычислим по формуле Бернулли величины
![]() ,
где
,
где![]() Имеем
Имеем
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Отсюда, получим следующий закон распределения:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
Теперь найдем математическое ожидание
![]() .
.
Найдем дисперсию и среднее квадратическое отклонение.
![]() .
.
![]() .
.
Заметте, что эти равенства легко определяются по теореме1 (см. (4)). Действительно,
![]() .
.
Пример 2 Устройство состоит из трех независимо работающих элементов. Вероятностьотказа каждого элемента в одном опыте равна 0,1.
1.Определить с.в.![]() и
составить закон распределения количества
отказавших элементов в одном опыте.
и
составить закон распределения количества
отказавших элементов в одном опыте.
2.Найти числовые характеристики данной случайной величины.
Решение. Дискретная случайная
величинаХ(число отказавших
элементов в одном опыте) имеет следующие
возможные значения:![]() (ни один из элементов устройства не
отказал),
(ни один из элементов устройства не
отказал),![]() (отказал один элемент),
(отказал один элемент),![]() (отказали два элемента) и
(отказали два элемента) и![]() (отказали три элемента).
(отказали три элемента).
Отказы элементов независимы один от
другого, вероятности отказа каждого
элемента равны между собой, поэтому
применима формула Бернулли. Учитывая,
что, по условию,
![]() получим:
получим:
![]()
![]()
![]()
![]()
Искомый биноминальный закон распределения случайной величины Х будет иметь вид:
|
X |
0 |
1 |
2 |
3 |
|
P |
0,729 |
0,243 |
0,027 |
0,001 |
Контроль-![]() .
.
Найдём математическое ожидание, дисперсию и среднее квадратическое отклонение по формулам (4) теоремы 1
![]()
Пример 3. Игральный кубик брошен 4 раза. Написать закон распределения числа появлений тройки.
Решение.Случайная величина может
принимать значения 0, 1, 2, 3, 4. Найдем их
вероятности по формуле Бернулли для![]() и
и![]() .
.
![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
Построим закон распределения рассмотренного примера
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
Контроль -![]() .
.
Задание.Вычислите математическое
ожидание, дисперсию и среднее
квадратическое отклонение случайной
величины![]() двумя
способами: по формулам (4) и по определению
этих величин.
двумя
способами: по формулам (4) и по определению
этих величин.
