18. Комбинационные устройства. Дешифраторы.

Под комбинационным устройством понимают устройство без запоминания переменных (логические схемы без памяти). Выходные переменные однозначно определяются значениями входных переменных. В слу­чае логических схем с памятью (схем последовательностного типа) выходные пере­менные зависят, кроме того, и от состоя­ния системы в данный момент, т.е. от ее предыстории, такие устройства называются последовательными.

Дешифратором называется комбинационное устройство, преобразующее n-разрядный двоичный код в логический сигнал, появляющийся на том выходе, десятичный номер которого соответствует двоичному коду. Обозначается на схемах как DC (DeCoder, шифратор – CD – CoDer). Число входов и выходов в так называемом полном дешифраторе связано соотношением m = 2ⁿ, где n — число входов, а m — число выходов. Если в работе дешифратора используется неполное число выходов, то такой дешифратор называется неполным. Так, например, дешифратор, имеющий 4 входа и 16 выходов, будет полным, а если бы выходов было только 10, то он являлся бы неполным.

Рассмотрим неполный дешифратор, реализующий код «1 из n», в данном случае, один из 10. Суть «кода 1 из n» в том, что в зависимости от входных сигналов (4 двоичных числа в нашем случае) на одном из выходов появляется логическая единица, соответствующая входному двоичному числу. Вид дешифратора и таблица переключений, характеризующая значения на выходах дешифратора, в зависимости от входных сигналов:

Число	Вход (A1…A4)	Выход(Y0…Y9)
0	0000	1000000000
1	0001	0100000000
2	0010	0010000000
3	0011	0001000000
4	0100	0000100000
5	0101	0000010000
6	0110	0000001000
7	0111	0000000100
8	1000	0000000010
9	1001	0000000001

Для такого дешифратора, функции выходов в зависимости от функций входов будут представлять собой следующие уравнения:

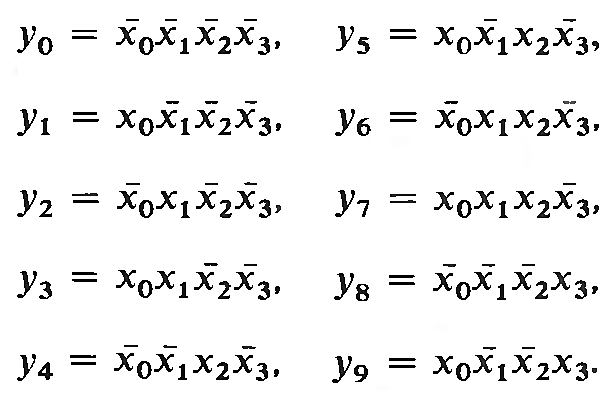
Схема такого дешифратора на логических элементах может быть построена очень просто по уравнениям, написанным выше: с помощью десяти элементов И с четырьмя входами (их выводы и есть выходы дешифратора). Входы элементов соединяются с соответствующими входами дешифратора, как в уравнении (с обычным входом, или с инвертированным). Но, стоит учесть, что в случае дешифратора 1 из 10, двоичных чисел на входах, выходящих за рамки диапазона от 0 до 9 в десятичной системе, быть не должно. Иными словами, на входы, для правильной работы, должны подаваться только такие значения, которые «умеет» расшифровывать дешифратор(какие есть в таблице переключений). В данном случае, не больше 1001 в двоичной системе, т.к. например, при 1101, на выходах мы получим нули. Для упрощения схемы, данные уравнения можно минимизировать с помощью карт Карно.

Преобразователями кодов в общем случае называются устройства, предназначенные для преобразования одного кода в другой, при этом они часто выполняют нестандартные преобразования кодов. Обозначаются обычно через X/Y. К таким преобразователям относится, например, преобразователь двоичного кода в код управления семисегментным индикатором. Принцип работы преобразователя схож с принципом работы дешифратора – в зависимости от входных сигналов, соответствующим образом формируются сигналы на выходах преобразователя кодов. Для описания работы преобразователя, также как и для дешифратора, пользуются таблицей переключений. Например, если на входы подаются двоичные сигналы (например со счетчика, в обычном двоичном коде – 8-4-2-1), а сигналы с выходов подаются на семисегментный индикатор, таблица переключений будет иметь вид (слева изображен преобразователь):

Число	Вход (1234)	Выход(abcdefg)
0	0000	1111110
1	0001	0110000
2	0010	1101101
3	0011	1111001
4	0100	0110011
5	0101	1011011
6	0110	1011111
7	0111	1110000
8	1000	1111111
9	1001	1111011

Внутренние компоненты преобразователя выбираются исходя из конкретного его предназначения. Чаще всего компоненты выбирают, составляя минимизированные логические уравнения для выходов преобразователя, которые в свою очередь находят с помощью составления карт Карно.

Кроме обычного двоично-десятичного кодирования чисел (по порядку 0-0000, 1-0001, 2-0010 и т.д. – 8-4-2-1), существуют и другие коды, например, код Айкена 2-4-2-1 (такой же как и 8-4-2-1 но 8-1110, 9-1111), 4-2-2-1, 5-4-4-1 и другие.