
Свойства дюрации и показателя выпуклости облигации.
Дюрация облигации не превосходит срока до ее погашения Т.
Действительно,
![]() ,
,
где P(r) – рыночная стоимость облигации в момент t = 0, r – ее внутренняя доходность.
Дюрация чисто дисконтной облигации равна сроку до ее погашения.
Действительно, для чисто дисконтной облигации имеем ,
где A – номинал облигации. Тогда дюрация облигации равна
 .
.
Если облигация не является чисто дисконтной, то чем больше внутренняя доходность облигации, тем меньше ее дюрация и показатель выпуклости.
Доказательство. Рассмотрим облигацию, по которой через t1 , t2,…, tn лет от текущего момента времени t = 0 (0 < t1 < t2 < … < tn ) обещают выплатить денежные суммы С1, С2,…, Сn соответственно. Безрисковые процентные ставки для всех сроков одинаковы и равны r. Покажем, что дюрация D и показатель выпуклости C облигации - это убывающие функции r. Согласно определению
 .
.
Рассмотрим производную

=
 .
.
Используем обозначения
![]() ,
,
![]() ,
,
![]() .
.
Покажем, что a2 – bc < 0 методом математической индукции по числу платежей n.
Основание индукции n = 2.
a2
– bc
=
 =
=
=
![]() ,
где t2
> t1.
,
где t2
> t1.
Предположим, что утверждение верно для ( n – 1 ) платежей по облигации, т.е.
![]() =
=
 .
.
Пусть теперь число платежей по облигации равно n. Рассмотрим
a2
– bc
=
 =
=
=
(
![]() )–
)–
![]() ,
,
где
![]() <
0 по
предположению индукции.
<
0 по
предположению индукции.
![]()
![]() ,
где 0
< t1
< t2
<…< tn.
,
где 0
< t1
< t2
<…< tn.
Следовательно
a2
– bc
<
0 для всех
целых
n
>
1. Значит,
![]() .
.
Согласно определению, показатель выпуклости равен
 .
.
Тогда
C
 =D
+ B,
=D
+ B,
где
 – дюрация облигации,
– дюрация облигации, .
Следовательно,
.
Следовательно,![]() ,
где
,
где![]() .
Покажем, что
.
Покажем, что![]() .
.
 .
.
Используем обозначения
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Покажем, что ab – dc < 0 методом математической индукции по числу платежей n.
Если n = 2, то


![]() ,
где 0
< t1
< t2.
,
где 0
< t1
< t2.
Положим,
![]() для (n
– 1 ) платежей по облигации, т.е.
для (n
– 1 ) платежей по облигации, т.е.
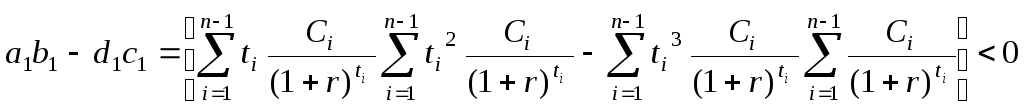 .
.
Для n платежей по облигации имеем
![]()
![]() .
.
![]() по
предположению индукции,
по
предположению индукции,
![]() =
=
=
 =
=
![]()
![]() ,
где
0
< t1
< t2
<…< tn.
,
где
0
< t1
< t2
<…< tn.
Значит,
ab
– dc
< 0 для
всех целых n
> 1.
Следовательно
![]() .
Тогда
.
Тогда![]() .
Свойство доказано.
.
Свойство доказано.
Если все платежи по облигации отсрочить на t0 лет, не изменяя ее внутренней доходности r, то дюрация облигации увеличится на t0 лет, а показатель выпуклости – на (t02 + 2 t0D + t0 ) лет2.
Доказательство. Дюрация исходной облигации
 .
.
Дюрация облигации с отсроченными платежами

=
 .
.
Таким образом,
![]() =
D
+ t0.
(11.12)
=
D
+ t0.
(11.12)
Показатель выпуклости исходной облигации
 .
.
Показатель выпуклости облигации с отсроченными платежами равен


= C + 2 t0D + t02 + t0 .
Таким образом,
![]() =
C
+ (t02
+ 2
t0D
+ t0
). (11.13)
=
C
+ (t02
+ 2
t0D
+ t0
). (11.13)
Свойство доказано.
Если до погашения облигации остается больше одного купонного периода, то при заданном значении внутренней доходности r дюрация облигации и показатель выпуклости тем больше, чем меньше купонная ставка.
Доказательство. Покажем, что дюрация облигации и показатель выпуклости – убывающие функции купонной ставки f .
Формула
(11.6) для дюрации купонной облигации,
продающейся через время
![]() после купонной выплаты с доходностью
к погашениюr,
когда до погашения остается n
купонных выплат, имеет вид:
после купонной выплаты с доходностью
к погашениюr,
когда до погашения остается n
купонных выплат, имеет вид:
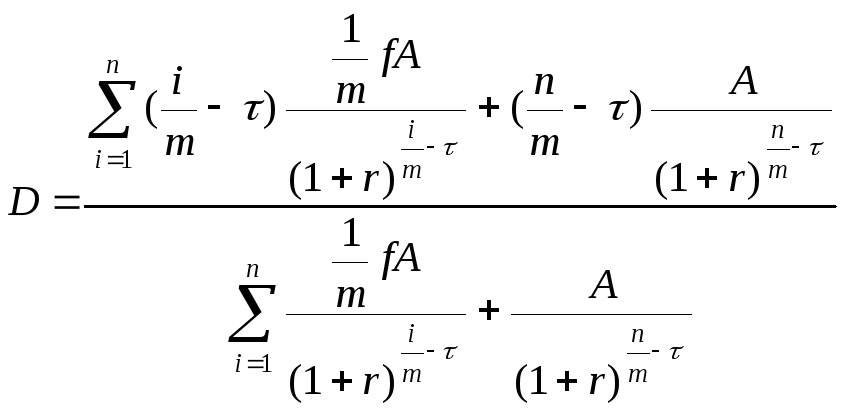 .
(11.14)
.
(11.14)
Цена облигации
 .
.
Используем обозначения
 .
(11.15)
.
(11.15)
Тогда
 .
.
Рассмотрим производную дюрации по купонной ставке f.

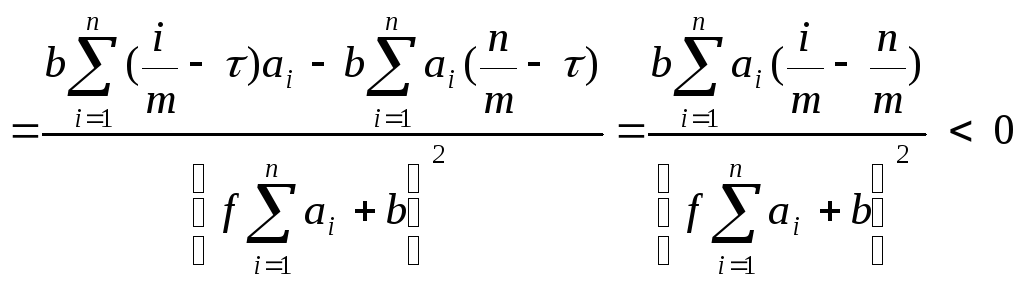 ,
,
так
как
![]() и по условиюn
> 1. Таким образом,
и по условиюn
> 1. Таким образом,
![]() .
.
Показатель выпуклости купонной облигации равен
 .
(11.16)
.
(11.16)
Используем те же обозначения (11.15). Тогда
C
=
 .
.
