
- •1.13. Инвестиции в портфель облигаций.
- •Пример 13.1. Сформирован портфель п(2000, 3000, 2000) из облигаций трех видов, потоки платежей по которым указаны в таблице. Определить поток платежей от этого портфеля.
- •1) Средневзвешенная доходность портфеля rср.; 2) внутренняя ставка доходности rP .
- •5. Если заданное значение дюрации портфеля d удовлетворяет условию
- •6. Иммунизирующее свойство дюрации портфеля.
- •Решение.
1.13. Инвестиции в портфель облигаций.
Дюрация и показатель выпуклости портфеля.
Рассмотрим портфель из облигаций, не имеющих кредитного риска. Риск неплатежа от портфеля отсутствует. Однако в условиях рынка остается процентный риск. Изменение процентных ставок на рынке вызывает изменение рыночных цен облигаций, входящих в портфель, а следовательно, изменение стоимости всего портфеля.
Предположим,
на рынке имеются облигации без кредитного
риска m
видов, цены которых в момент t
= 0 равны соответственно P1,
P2,…,
Pm.
Предположим также, что на рынке можно
купить любое количество облигаций, в
том числе нецелое. Пусть Ωj
– сумма, затраченная инвестором на
приобретение облигаций j
– го вида, j
= 1, 2,…, m.
Тогда в момент t
= 0 сформирован портфель облигаций П(Ω1,
Ω2,…,
Ωm),
стоимость которого равна Ω =
![]() .
kj
=
.
kj
=
![]() и
и
![]() – соответственно количество и доля
облигаций j
– го вида в портфеле, j
= 1, 2,…, m.
Следовательно,
– соответственно количество и доля
облигаций j
– го вида в портфеле, j
= 1, 2,…, m.
Следовательно,![]() . Пусть через t1,
t2,…,
tn
лет от момента t
= 0 производится
платеж хотя бы по одному виду облигаций,
входящих в портфель. Обозначим через
. Пусть через t1,
t2,…,
tn
лет от момента t
= 0 производится
платеж хотя бы по одному виду облигаций,
входящих в портфель. Обозначим через
![]() платеж по облигации j
– го вида в момент ti,
где i
= 1, 2, …, n.
Тогда R1,
R2,
…, Rn
в моменты t1,
t2,…,
tn
–
ожидаемый
поток платежей от портфеля, где
платеж по облигации j
– го вида в момент ti,
где i
= 1, 2, …, n.
Тогда R1,
R2,
…, Rn
в моменты t1,
t2,…,
tn
–
ожидаемый
поток платежей от портфеля, где
![]() ,
i
= 1, 2, …, n.
(13.1)
,
i
= 1, 2, …, n.
(13.1)
Таким образом, портфель П(Ω1, Ω2,…, Ωm) в момент t = 0 можно рассматривать как одну облигацию без кредитного риска стоимостью Ω с потоком платежей R1, R2, …, Rn в моменты времени t1, t2,…, tn. По своим инвестиционным качествам портфель эквивалентен такой облигации.
Пример 13.1. Сформирован портфель п(2000, 3000, 2000) из облигаций трех видов, потоки платежей по которым указаны в таблице. Определить поток платежей от этого портфеля.
|
Облигация |
Платеж, д.е. |
||||
|
Срок, годы |
|||||
|
0 |
0,5 |
1 |
1,5 |
2 |
|
|
В1 |
- 850 |
|
|
|
1035 |
|
В2 |
- 290 |
10 |
10 |
330 |
|
|
В3 |
- 990 |
|
90 |
|
1100 |
Согласно условию, P1 = 850, P2 = 290, P3 = 990; Ω1 = 2000, Ω2 = 3000, Ω3 = 2000. Члены потока платежей от портфеля рассчитаем по (13.1):
R1
=
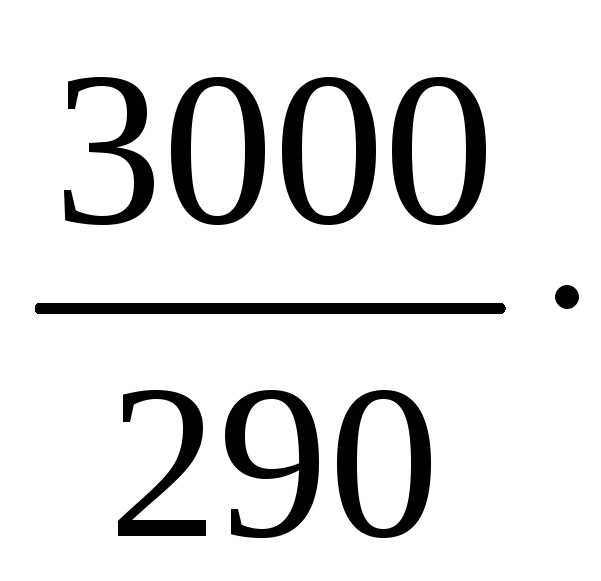 10
= 103,448 в момент t1
= 0,5.
10
= 103,448 в момент t1
= 0,5.
R2
=
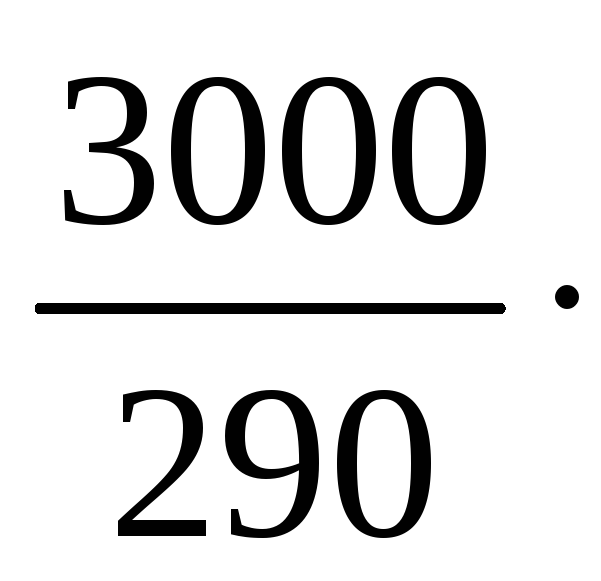 10
+
10
+
 90
= 285,266 в момент t2
= 1.
90
= 285,266 в момент t2
= 1.
R3
=
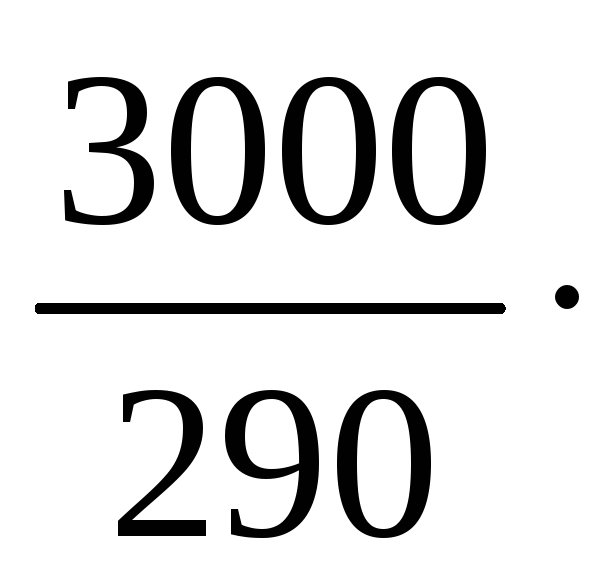 330
= 3413,793 в момент t3
= 1,5.
330
= 3413,793 в момент t3
= 1,5.
R4
=
 1035
+
1035
+
 1100
= 4657,516 в момент t4
= 2.
1100
= 4657,516 в момент t4
= 2.
Таким образом, поток платежей от портфеля П(2000, 3000, 2000) имеет вид, показанный в таблице:
|
Срок, годы |
0 |
0,5 |
1 |
1,5 |
2 |
|
Платеж, д.е. |
- 7000 |
103,448 |
285,266 |
3413,793 |
4657,516 |
Меры доходности портфеля.
Для вычисления доходности портфеля П(Ω1, Ω2,…, Ωm) приняты две характеристики:
