59

ЛЕКЦИЯ №5

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

1. Понятие о колебательном движении.

Гармонические колебания.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Колебательное движение и вызываемые им волны очень часто встречаются в природе и технике. Колеблются мосты под действием проходящих по ним поездов, совершает колебания барабанная перепонка уха, вибрируют части зданий, ритмично сокращается сердечная мышца.

В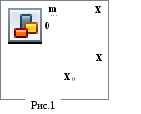зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные и др.. Мы рассмотрим механические колебания.

Рассмотрим простейшую механическую систему, состоящую из тела (шар) некоторой массы m, нанизанного на стержень, и пружины с жёсткостью k, соединяющей его с неподвижной стеной. Направим ось OX вдоль стержня, а начало координат совместим с центром шара, при условии, что пружина находится в недеформированном состоянии. Сместим шар на расстояние X₀ от положения равновесия (см. рис.1). Тогда со стороны пружины на тело будет действовать упругая сила F=-kX₀ (1). Эта сила, как видно из уравнения (1), пропорциональна смещению и направлена в сторону противоположную смещению. Её называют возвращающей силой. Кроме того, система будет обладать запасом потенциальной энергии . Если отпустить груз, то под действием упругой силы он станет двигаться к положению равновесия, при этом его потенциальная энергия будет уменьшаться, переходя в кинетическую, возвращающая сила будет убывать и в положении равновесия станет равной нулю, но тело в положении равновесия не остановиться, а по инерции будет продолжать движение. Его кинетическая энергия будет переходить в потенциальную, возвращающая сила станет расти, но её направление изменится на противоположное. В системе возникнут колебания. При колебательном движении положение тела в каждый данный момент времени характеризуется расстоянием от положения равновесия, которое называется смещением. Среди различных видов колебаний наиболее простой формой является гармоническое колебание, т.е. такое, при котором колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.

2. Незатухающие гармонические колебания.

Пусть на тело массой m действует сила, стремящаяся вернуть его в положение равновесия (возвращающая сила) и пропорциональная смещению от положения равновесия, т.е. сила упругости F_УПР= -kX . Если трение отсутствует, тогда уравнение второго закона Ньютона для тела имеет вид:

; или .

Обозначим , получим. (1)

Уравнение (1) является линейным однородным дифференциальным уравнением 2-го порядка, с постоянными коэффициентами. Решение уравнения (1) будет законом свободных или собственных незатухающих колебаний:

,

где A – величина наибольшего отклонения от положения равновесия, которая называется амплитудой (амплитуда – постоянная, положительная величина); - фаза колебаний;- начальная фаза.

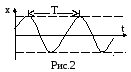Графически незатухающие колебания представлены на рис.2:

Т – период колебания (промежуток времени одного полного колебания); , где - круговая или циклическая частота,, ν называется частотой колебания.

Чтобы найти скорость материальной точки при гармоническом колебании, нужно взять производную от выражения для смещения:

,

где - максимальная скорость (амплитуда скорости). Продифференцировав это выражение, найдём ускорение:

,

где - максимальное ускорение.

3. Затухающие гармонические колебания.

В реальных условиях, кроме возвращающей силы в колеблющейся системе будет действовать сила трения (сила сопротивления среды), которая при небольших скоростях пропорциональна скорости движения тела: , гдеr – коэффициент сопротивления. Если ограничиться учётом возвращающей силы и силы трения, то уравнение движения примет вид: или , разделив наm, получим: , обозначив ,, получим:. Это уравнение носит название линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решение этого уравнения будет законом свободных затухающих колебаний, и будет иметь следующий вид: .

Из уравнения видно, что амплитуда не является постоянной, а зависит от времени и убывает по экспоненциальному закону. Как и для незатухающих колебаний, величина ω – называется круговой частотой:, где- коэффициент затухания;

-начальная фаза.

Графически затухающие колебания представлены на рис.3.

О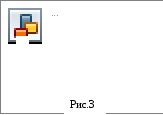пределим период колебанийили, откуда видно, что колебания в системе могут возникать только при условии если сопротивление незначительно. Период колебаний практически равен.

С ростом коэффициента затухания, период колебаний увеличивается и при обращается в бесконечность. Движение перестаёт быть периодическим. Выведенная из положения равновесия система возвращается в состояние равновесия, не совершая колебаний. Такое движение называется апериодическим.

На рис.4 показан один из случаев возвращения системы в положение равновесия при апериодическом движении. В соответствии с указанной кривой спадает заряд на мембранах нервных волокон человека.

Для характеристики скорости затухания колебаний вводится понятие коэффициента затухания . Найдём время τ, за которое амплитуда колебаний уменьшится вe раз:

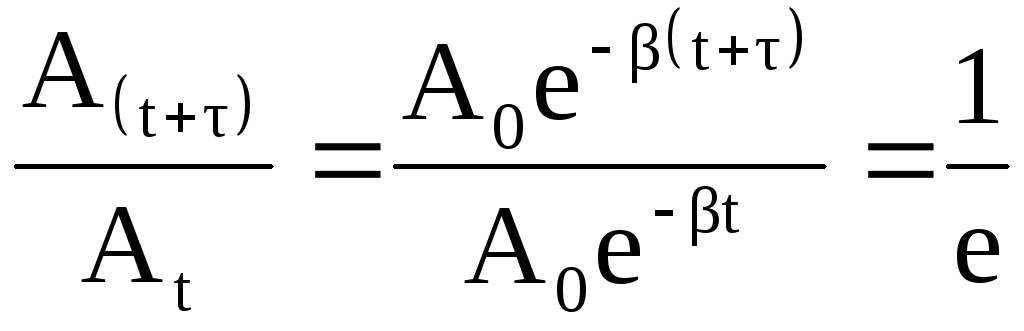, т.е.

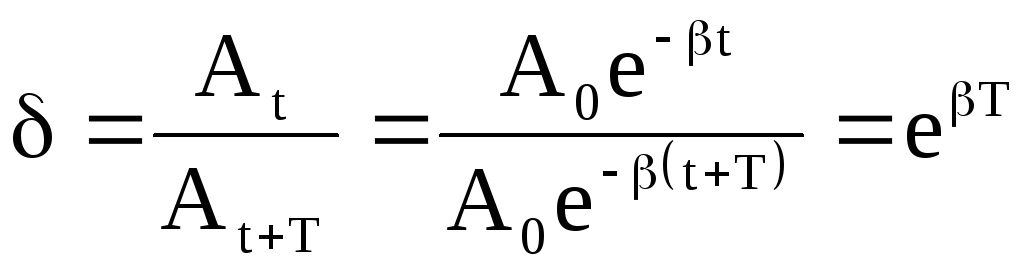откуда βτ=1, следовательно . Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшится вe раз. Отношение значений амплитуд, соответствующих моментам времени, отличающихся на период, равное называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:

.