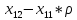15. Методи виявлення та усунення автокореляції залишків.

Методи виявлення автокореляції залишків:

І Графічний метод

Будується модель і статистичні точки, на основі яких побудована модель. По розміщенні точок навколо моделі можна судити про наявність і відсутність автокореляції.

ІІ Тест Дарбіна-Уотсона

Обчислюємо параметр Дарбіна – Уотсона

Знаходимо в таблиці числа . Ці числа залежать від рівня значущості α, довжини статистичного ряду n і кількості коефіцієнтів моделі – m.

За допомогою табличних будуємо інтервал.

На побудований інтервал наносимо число «d»:

• Число d попадає в проміжок «А» - автокореляція відсутня;

• В1 – присутня відємна автокореляція;

• В2 – присутня додатня автокореляція

• С – зона невизначеності – це говорить про те, що даний метод не може дати точної відповіді (присутня чи відсутня автокореляція).

Усунення автокореляції:

• Правильна специфікація моделі (якщо це можливо)

• Обчислюємо автокореляційний коефіцієнт

Необхідно перерахувати заново усі статистичні дані

…	…	…

• На основі нової таблиці будуємо нову модель, у якої, можливо, автокореляція вже відсутня.

16. Гетероскедатичність залишків, причини виникнення, наслідки, методи виявлення.

Трапляються такі випадки, коли дисперсія залишків є величина не постійна, таке явище називається гетероскедатичність.

Причини виникнення:

• Неправильна специфікація моделі (неправильно визначено тип функціональної залежності або в модель не включено деякий фактор, який суттєво впливає на залежну змінну).

• Накопичення похибок вимірювання даних або не удосконалення методики збору статистичної інформації.

Наслідки: необґрунтоване збільшення довірчих інтервалів, що призводить до неефективних прогнозів.

Методи виявлення:

І Графічний метод

ІІ Виявити гетероскедатичність можна якщо виконати наступні кроки:

• Ранжуємо статистичний ряд по змінних x;

• Розбиваємо статистичний ряд на 2 рівні частини (якщо довжина статистичного ряду досить велика (), то можна відсунути деяку незначну за розміром середню частину, в цьому випадку ефективність тесту посилюється);

• На основі отриманих даних будуємо 2 моделі.

• Для кожної моделі знаходимо суми:

Обчислюємо F–стат. Після чого більше число ділимо на менше.

Порівнюємо обчислюване значення F із табличним, якщо F, то гетероскедатичність присутня.

17. Методи виявлення та усунення гетероскедатичності.

Методи виявлення:

І Графічний метод

ІІ Виявити гетероскедатичність можна якщо виконати наступні кроки:

• Ранжуємо статистичний ряд по змінних x;

• Розбиваємо статистичний ряд на 2 рівні частини (якщо довжина статистичного ряду досить велика (), то можна відсунути деяку незначну за розміром середню частину, в цьому випадку ефективність тесту посилюється);

• На основі отриманих даних будуємо 2 моделі.

• Для кожної моделі знаходимо суми:

• Обчислюємо F–стат. Після чого більше число ділимо на менше.

Порівнюємо обчислюване значення F із табличним, якщо F, то гетероскедатичність присутня.

Методи усунення:

• Якщо це можливо, то необхідно правильно ідентифікувати модель;

• Чітко знати від якої змінної х є залежність дисперсії залишків;

• Необхідно знати як дисперсія залишків залежить від змінної х.

Нехай побудована трьох факторна модель:

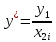; ; ;, тоді модель набуває такого вигляду:

Тобто будуємо нову модель по таблиці нових даних і коефіцієнти цієї моделі підставляємо в стару модель.