5.Основні теореми двоїстої та їх економічний зміст.

Зв’язок між оптимальними розв’язками прямої та двоїстої задач встановлюють леми та теореми двоїстості.

Основна нерівність теорії двоїстості. Якщо та — допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність або .

Доведення. Помножимо кожне рівняння системи на відповідну змінну двоїстої задачі:

Маємо:

Підсумувавши праві і ліві частини нерівностей, отримаємо:.

Аналогічно перетворимо систему обмежень двоїстої задачі:

Підсумувавши після множення тут також ліві та праві частини, отримаємо нерівність: .

Ліві частини нерівностей та збігаються, отже: .

Нерівність доведено.

Достатня умова оптимальності. Якщо та — допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність то X*, Y* — оптимальні розв’язки відповідних задач.

Доведення. Нехай — допустимий план прямої задачі. Тоді на підставі нерівності маємо: . За умовою задачі , отже

Оскільки за допущенням — довільний допустимий план прямої задачі, то нерівність виконується для будь-якого з можливих розв’язків. Отже, маємо, що при цільова функція набирає найбільшого значення, тобто є оптимальним розв’язком початкової задачі.

В аналогічний спосіб доводиться, що — оптимальний план двоїстої задачі.

6.Базисний та опорний розв’язки задачі лінійного програмування. Штучний базис задачі лінійного програмування.

Базисний розв'язок складається з базисних змінних і нулів, причому нулям відповідають небазисні змінні. Якщо в базисі є стільки змінних, скільки рівнянь, то такий базис називається не виродженим. Якщо ж базисних змінних менше, то такий базис називається виродженим.

Якщо базисний розв’язок задачі не містить від’ємних чисел, то він називається опорним.

Більшість задач не можна звести до потрібного вигляду. В такому разі застосовується метод штучного базису.

Розглянемо задачу лінійного програмування:

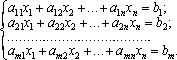
Задача подана в канонічному вигляді і система обмежень не містить одиничної матриці. Отримати одиничну матрицю можна, якщо до кожного рівняння в системі обмежень задачі додати одну змінну . Такі змінні називають штучними. (Не обов’язково кількість введених штучних змінних має дорівнювати m. Їх необхідно вводити лише в ті рівняння системи обмежень, які не розв’язані відносно базисних змінних.) Допустимо, що система рівнянь не містить жодного одиничного вектора, тоді штучну змінну вводять у кожне рівняння:

7.Задачі цілочисельного програмування та методи їх розв’язку.

У багатьох задачах оптимального планування значення невідомих вказує на кількість одиниць того чи іншого обладнання, автомашин і т.д., тобто є цілими числами. Задачі лінійного програмування, у яких допустимі множини включають також вимогу цілочисельності всіх змінних, називаються задачами цілочисельності лінійного програмування.

Прикладом математичної моделі такої задачі є:

max(min)Z=

Де N – деяка множина множини (1,2,…,m).

Якщо N=(1,2,3,…,n), то ця задача повністю цілочисельного лінійного програмування, у протилежному випадку – задача частково цілочисельного лінійного програмування.