Змінимо напрям реакції на протилежний на кресленні та відповідно знак реакції на протилежний. Тоді будемо мати

З рівняння моментів відносно точки В

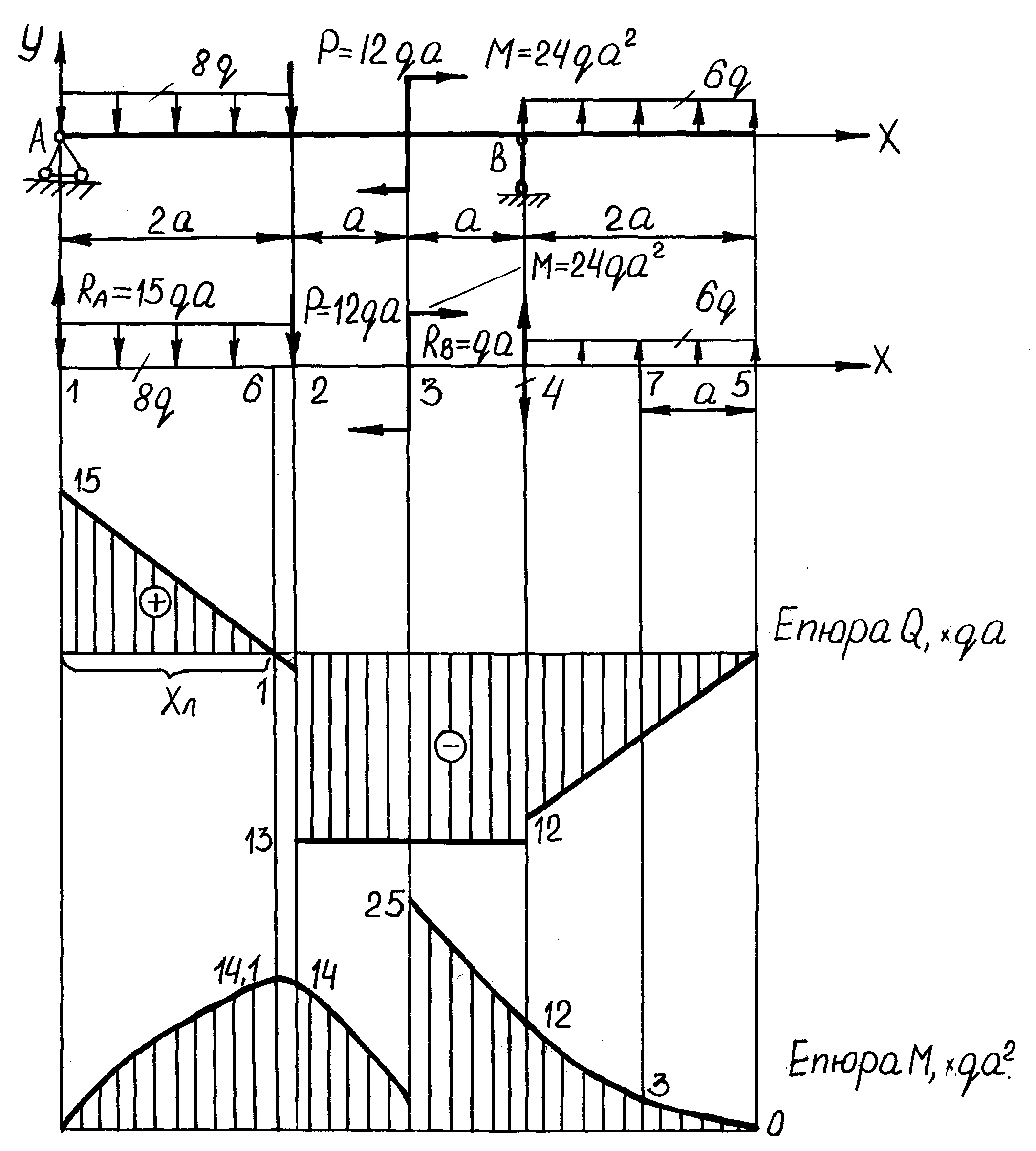
Мал.23

Знаходимо

Перевірка: ;

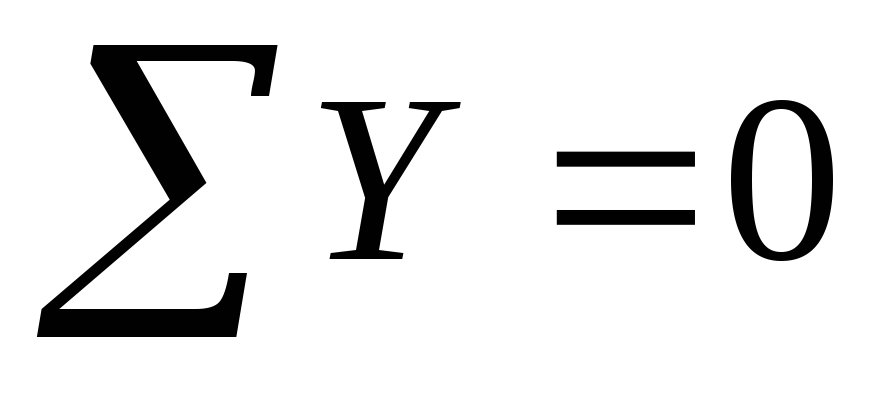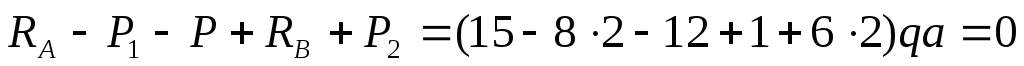
Одержана тотожність говорить про те, що обчислення реакцій зроблено правильно.

Поперечні сили:

;

;

;

У перерізах 4-5 поперечні сили зручніше визначити справа-наліво (знаки при цьому змінюються на протилежні).

; .

Перевірка: (те ж, що зліва-направо)

Епюра Q . Поле епюри

Після побудови виконуємо перевірку "векторним способом": у пере­різах під силами є "стрибки" на величину цих сил у напрямку їх дій. На дільницях з розподіленими навантаженнями епюра Q - похила пря­ма. Момент М не впливає на епюру Q . Правило замкнутості епюри також виконується: починаючи з нульового значення у лівому кінцево­му перерізі: епюра закінчується на нуль у правому кінцевому перерізі.

Визначаємо згинаючі моменти

; . Оскільки на ділянці 1-2 епюра Q перетинає базис, визначимо екстремальне значення моменту у перерізі, для якого поперечна сила дорівнює нулю. Абсциса точки 6 та момент

;

.

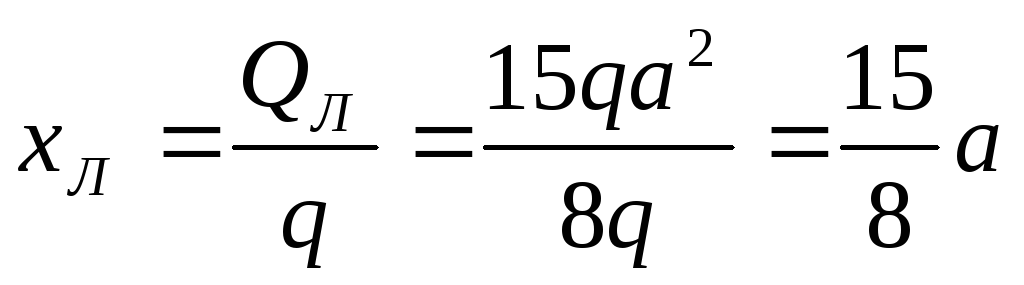Епюру M на ділянці 1-2 можна будувати по значеннях згинаю­чих моментів в точках 1, 2, 6.

.

Для останніх перерізів зручніше визначити згинаючі моменти розгляданням справа-наліво:

;

Для побудови параболи визначимо момент у перерізі на середині прольоту (в т.7), тобто на відстані a від правого кінця:

.

Епюра Q не перетинає базис, тому не повинно бути екстремуму M.

Перевірка: .

Епюра M . Поле епюри:

Перевірка епюри M: у перерізі під моментом - стрибок на величину моменту на дільницях з рівномірно розподіленим навантаженням епюри M - парабола з випуклістю проти напряму дії навантаження; на ділянках між навантаженнями епюри - нахилені прямі.

Небезпечним є переріз 3 , в якому діє максимальний момент і максимальна поперечна сила .

Завдання 6. Двотаврова балка № 16 (мал.24) навантажена згинаючим моментом , зосередженою силою , рівномірно розподіленим навантаженням інтенсивністю . Перевірити міцність балки по нормальним напруженням

Розв’язок

1.Опорні реакції:

; ;

;

; ; .

Перевірка: .

2.Поперечні сили.; ;

.

Епюра Q . Поле епюри: .

Мірило .

3.Згинаючі моменти.

; ; ;

Справа-наліво: ; ;

.

Перевірка: .

Епюра M . Поле епюри . Мірило .

Небезпечний переріз - точка 2, у якому , .

Рівняння міцності:

Для двотавра №16 по ГОСТ 8239-72

Мал.24

Фактичні напруження

.

Відхилення

- недонапруження, тобто міцність балки забезпечена.

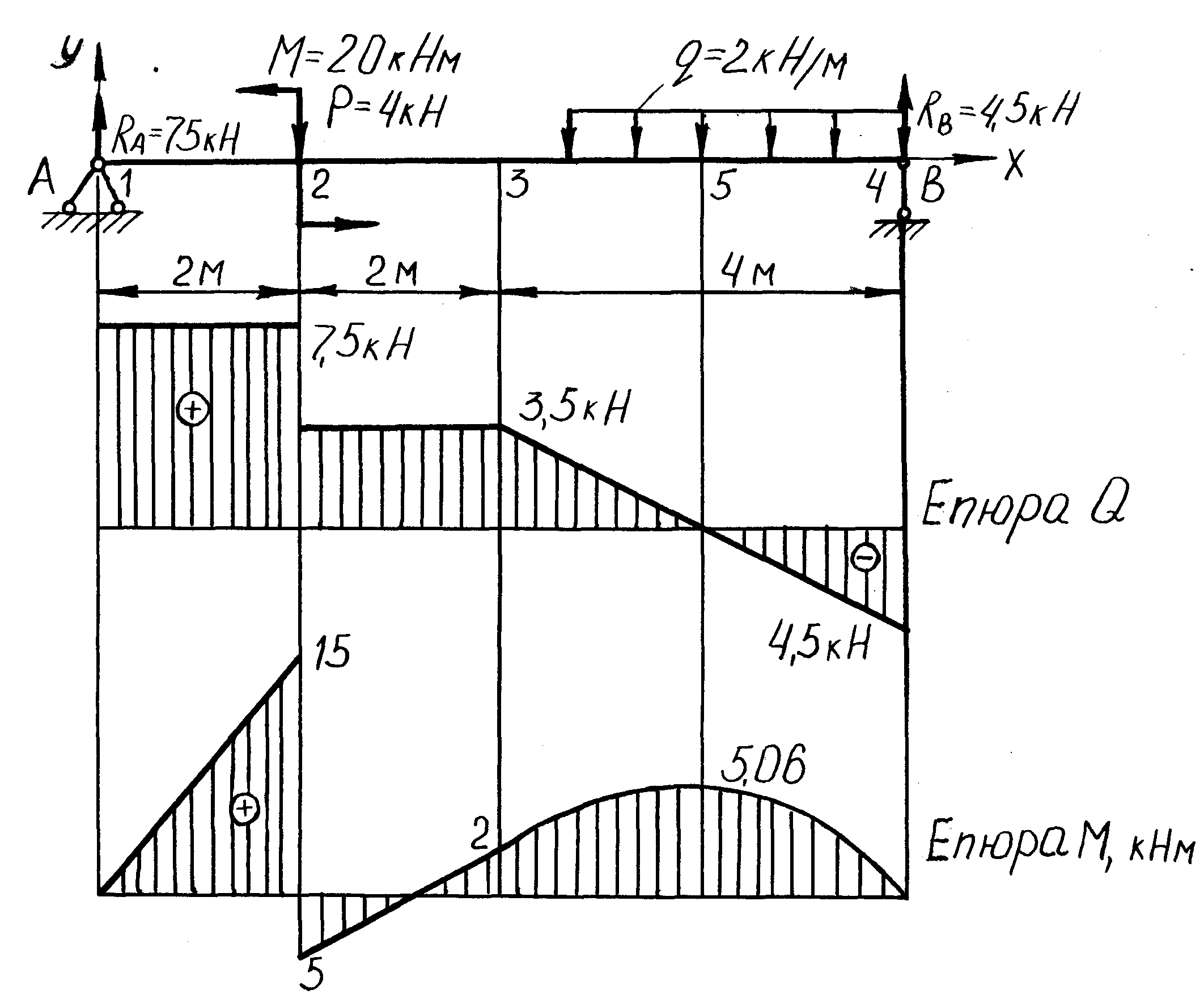
Завдання №7. Дано: ; , ; (мал.25). Побудувати епюри Q та M . Визначити необхідні розміри круглого, квадратного, прямокутного ( ), швелерного та двотаврового перерізів.

Приклад рішення.

Опори балки - А і В. Характерні перерізи 15.

1.Опорні реакції.

; ;

;

; ;

.

Перевірка: ; ;

;

2.Поперечні сили.

;;

;

; .

Епюра Q . Поле епюри .

3.Згинаючі моменти: ; ;

;

Справа-наліво: .

Перевірка: .

Епюра М . Поле епюри: . .

4.Допустимі напруження

Приймаємо

.

5.Підбір перерізів. Рівняння міцності ;

.

а) круглий переріз ; ;

По ГОСТ 2590-71 приймаємо .

Мал.25

б) квадратний переріз ; ;

По ГОСТ 2591-71 приймаємо .

.

в) прямокутний переріз ; ;

; Приймаємо ; ; г) швелерний переріз

По ГОСТ 8240-72 для швелера №12 ; для №14 - .

Перевіряємо швелер №12

.

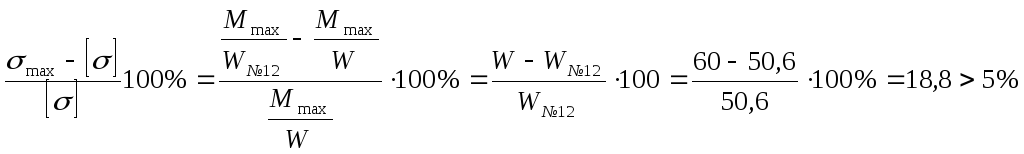Швелер №12 брати не можна так як перенапруга > 5%.

Перевіряємо швелер №14.

.

Приймаємо швелер №14.

д) двотавровий переріз

По ГОСТ 8239-72 для двотавра №12 , для двотавра №14 – . Перевіряємо двотавр №12. тобто перенапруження

меньше 5%, що допустимо. Приймаємо двотавр №12.

СКЛАДНИЙ ОПІР.

По цьому розділу курсу виконується завдання "Розрахунок на міцність вала при згині і крученні", яке складається з двох задач. Розраховуються вали циліндричної косозубої та конічної передач. Роз­рахункові схеми задач враховують одночасну дію кручення, згину, розтягу або стиску. Тобто внутрішні зусилля в поперечному перерізі приводяться до таких компонентів: крутного моменту відносно осі вала, моменту згину та відносно головних цен­тральних вісей симетрії перерізу Y та Z , поперечних сил та , спрямованих по тим же вісям та повздовжньої сили , діючій вздовж осі х.

Дотичні напруження, визначаючі та , мають другорядне значення і їх при розрахунку звичайно не враховують. Дією осьових сил також нехтують.

Для відшукання небезпечного перерізу вала необхідно побуду­вати епюри внутрішніх силових факторів – крутного момента та моментів згину та . Розрахунок на міцність ведуть по еквівалентному напруженню для небезпечної точки перерізу. Небезпечною є точка, для якої еквівалентне напруження має найбільше значення. В небезпечних точках при зазначеному сполученні деформацій має місце спрощений напружений стан. Еквівалентне напруження можна визначити в залежності від прийнятої теорії міцності по одній з наступних формул:

;

Небезпечний буде переріз для якого має найбільше значення. В цьому перерізі небезпечними є точки, які найбільш віддалені від нейтральної вісі, поскільки найбільші напруження та виникають в периферійних точках перерізу. Умова міцності має вигляд: За цією формулою розрахунки круглих валів ведуть аналогічно роз­рахункам на згин, але не по згинаючому, а по еквівалентному моменту. Вали звичайно виготовлюють із матеріалів, для яких

Приклади розв’язування завдань

Приклад І. Побудувати епюри моментів згину та кручення, визна­чити опорні реакції та діаметр вала редуктора. Провести розрахунок при ;

, (мал. 26)

Розв'язок.

Складемо розрахункову схему. Сили, паралельні осі .вала, нази­вають

осьовими , дотичні до ділільних кіл коліс – дотичними , діючі

вздовж радіуса до центру коліс – радіальними

Розглянемо рівновагу вала, перед цим приводячи сили , та , до центру вала. Використовуючи правило паралельного перено­су сил, одержимо на схемі вала окрім перерахованих сил моменти кру­чення :

и

від переносу дотичних сил та відповідно, а також момент згину

від переносу осьової сили (мал. 28)

Моменти m₁ та m₂ спричиняють кручення вала відносно вісі х на проміжках від лівого кінця вала до середини зубчатого колеса (між перерізами Д та C) , а момент згину від сили - згин в площині

Так як сила невідома, знайдемо її. Складемо рівняння рівноваги - суму моментів всіх сил відносно вісі X

Мал.26

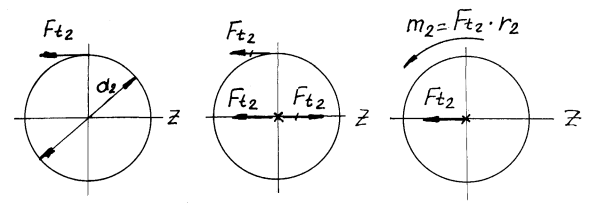
Мал. 27

56