
1212
.docxМетод 2МНК можна застосовувати бля оцінки параметрів:
Select one:
 a.
точно ототожненого рівняння
a.
точно ототожненого рівняння
![]()
 b.
неможливо використовувати в будь-якому
випадку
b.
неможливо використовувати в будь-якому
випадку
 c.
переототожненого рівняння
c.
переототожненого рівняння
 d.
недеототожненого рівняння
d.
недеототожненого рівняння
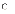 e.
у випадку рекурсивних моделей
e.
у випадку рекурсивних моделей
Question 2
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
Діаграма розподілу це:
Select one:
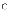 a.
інша назва множинної прогресії
a.
інша назва множинної прогресії
 b.
лінія з нахилом а і перетином b
b.
лінія з нахилом а і перетином b
 c.
графік значень незалежної і залежної
змінних
c.
графік значень незалежної і залежної
змінних
 d.
інша назва простої прогресії
d.
інша назва простої прогресії
 e.
лінія, що відображає зв'язок між незалежною
і залежною змінними
e.
лінія, що відображає зв'язок між незалежною
і залежною змінними
![]()
Question 3
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
При перевірці значимості параметра регресії використовуємо:
Select one:
 a.
будь-що із згаданого тут
a.
будь-що із згаданого тут
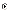 b.
X2-
тест
b.
X2-
тест
![]()
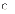 c.
t - тест
c.
t - тест
 d.
F-тест
d.
F-тест
 e.
біноміальний розподіл
e.
біноміальний розподіл
Question 4
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
Якщо ми будуємо взаємозв’язок, котрий має U-подібний вигляд (такий, як крива загальних витрат), найкраще відобразити його за допомогою:
Select one:
 a.
залежної
змінної
з
лагом
a.
залежної
змінної
з
лагом
 b.
атрибутивної
змінної
b.
атрибутивної
змінної
![]()
 c.
квадратичної
регресійної
моделі
c.
квадратичної
регресійної
моделі
 d.
такий зв'язок не може бути відображений
за допомогою регресійного аналізу
d.
такий зв'язок не може бути відображений
за допомогою регресійного аналізу
 e.
простої
регресії
e.
простої
регресії
Question 5
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
Припустимо, що залежність витрат від доходу описується функцією:
а b0=3. Тоді коефіцієнт еластичності витрат від доходу дорівнює:
Select one:
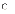 a.
4
a.
4
 b.
1
b.
1
 c.
9
c.
9
![]()
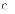 d.
8
d.
8
Question 6
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
Припустимо, що залежність витрат від доходу описується функцією:
Середнє значення y=15, середнє значення x=7, а b1=4. Тоді коефіцієнт еластичності витрат від доходу дорівнює:
Select one:
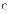 a.
1/7
a.
1/7
 b.
4
b.
4
![]()
 c.
38
c.
38
 d.
9
d.
9
Question 7
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
За інших однакових умов, чим більша оцінка середнього квадратичного відхилення нахилу, тим:
Select one:
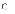 a.
більший
коефіцієнт
нахилу
a.
більший
коефіцієнт
нахилу
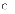 b.
більша величина перетину
b.
більша величина перетину
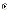 c.
менша t-величина нахилу
c.
менша t-величина нахилу
![]()
 d.
більша t-величина нахилу
d.
більша t-величина нахилу
 e.
менша t-величина перетину
e.
менша t-величина перетину
Question 8
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
При перевірці значимості коефіцієнта регресії (b1 ) нульова гіпотеза представлена:
Select one:
 a.
H0 : β1
a.
H0 : β1
![]()
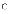 b.
-0.5
b.
-0.5
 c.
-1
c.
-1
 d.
H0 : β1
d.
H0 : β1
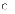 e.
H0 : β1
e.
H0 : β1
 f.
0.5
f.
0.5
 g.
H0 : β1
g.
H0 : β1
 h.
1
h.
1
 i.
H0 : β1
i.
H0 : β1
 j.
0
j.
0
Question 9
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
Крива Філіпса краще за все описується моделлю:
Select one:
 a.
a.
 b.
b.
 c.
c.
![]()
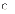 d.
d.
Question 10
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
Щоб перевірити, чи є нахил позитивним і таким, що значимо відрізняється від нуля, нульова гіпотеза має бути такою:
Select one:
 a.
H0 : β1
a.
H0 : β1
 b.
H0 : β1
b.
H0 : β1
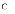 c.
0
c.
0
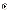 d.
H0 : β1≤0
d.
H0 : β1≤0
![]()
 e.
1
e.
1
 f.
H0 : β1 ≥1
f.
H0 : β1 ≥1
 g.
H0 : β1≥0
g.
H0 : β1≥0
Question 11
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
У регресії завжди має бути:
Select one:
 a.
r > 0
a.
r > 0
 b.
r < 0
b.
r < 0
 c.
t < 0
c.
t < 0
![]()
 d.
d.
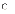 e.
t > 0
e.
t > 0
Question 12
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
Що з наведеного не є припущенням моделі лінійної регресії
Select one:
 a.
дисперсія випадкової величини дорівнює
0
a.
дисперсія випадкової величини дорівнює
0
 b.
випадкові величини є статистично не
залежними одна від одної
b.
випадкові величини є статистично не
залежними одна від одної
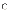 c.
або є сталими числами, або вони є
статистично незалежними від
випадкових величин Ei
c.
або є сталими числами, або вони є
статистично незалежними від
випадкових величин Ei
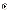 d.
математичне сподівання випадкової
величини Ei
дорівнює нулеві
d.
математичне сподівання випадкової
величини Ei
дорівнює нулеві
![]()
 e.
дисперсія випадкової величини Ei
e.
дисперсія випадкової величини Ei
Question 13
Incorrect
Mark 0,00 out of 1,00
 Flag
question
Flag
question
Question text
Крива витрат Енгеля показує відношення витрат споживача до його загального доходу. Позначаючи через У витрати споживача на товари, через Х доход споживача, отримує такі моделі:
Select one:
 a.
a.
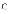 b.
b.
 c.
c.
![]()
 d.
d.
Question 14
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
Рівняння симультативної моделі переототожнене, якщо :
Select one:
 a.
K - k ≥ m – 1 і ранг матриці А менший за М-1
a.
K - k ≥ m – 1 і ранг матриці А менший за М-1
 b.
m – 1 і ранг матриці А дорівнює М-1
b.
m – 1 і ранг матриці А дорівнює М-1
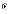 c.
K - k > m – 1 і ранг матриці А буде дорівнювати
М–1
c.
K - k > m – 1 і ранг матриці А буде дорівнювати
М–1
![]()
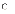 d.
K - k < m – 1, ранг матриці А менший за М-1
d.
K - k < m – 1, ранг матриці А менший за М-1
 e.
K - k
e.
K - k
Question 15
Correct
Mark 1,00 out of 1,00
 Flag
question
Flag
question
Question text
Рівняння симультативної моделі:
Select one:
 a.
завжди можна пере ототожнити
a.
завжди можна пере ототожнити
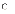 b.
завжди можна точно ототожнити
b.
завжди можна точно ототожнити
 c.
можливі будь-які варіанти
c.
можливі будь-які варіанти
![]()
 d.
завжди можна недоототожнити
d.
завжди можна недоототожнити
