З урахуанням виразу :

. (2.36)

Згідно з законом Майєра і співвідношення, (2.36) можна представити у вигляді:

. (2.37)

Підставляючи із рівнянь стану значення і, отрмаємо:

. (2.38)

З урахуванням 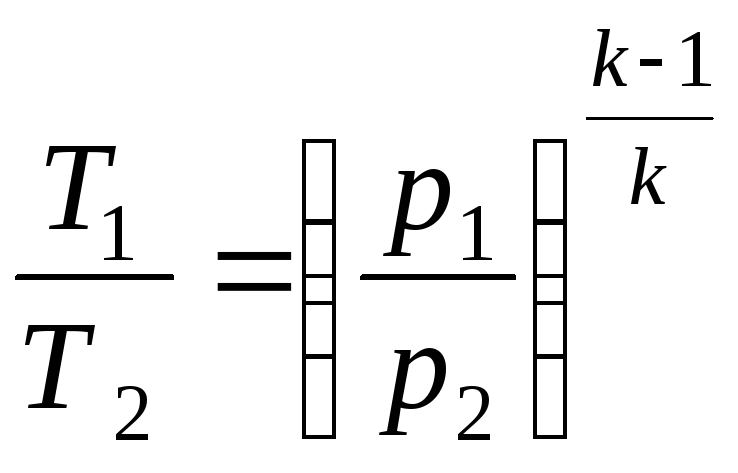, вираз (2.38) можна представити у вигляді:

. (2.39)

Таким чином, робота розширення в адіабатному процесі виконується за рахунок зменшення внутрішньої енергії газу, а його температура зменшується .

Коефіцієнт розподілу теплоти в процесі q=0:

. (2.40)

Теплоємність адіабатного процесу

. (2.41)

Показник адіабати для одноатомних газів дорівнюєk=1,66, для двохатомних k=1,4 і для трьохатомних k=1,3.

Зміна кількості теплоти , тому щоТ, атоі. Таким чином, адіабатний процес з ідеальним газом є ізоентропійний процес.

Політропний процес і його узагальнююче значення. Політропні процеси – це рівноважні, оборотні процеси, що протікають при постійній теплоємності c=const.

Кожен політропний термодинамічний процес (ТП) має цілком визначений, властивий йому характер розподілу енергетичних складових, що входять у рівняння першого закону термодинаміки: , Дж/кг.

Політропний процес – це процес зміни стану робочого тіла, у якому у внутрішню енергію протягом усього процесу перетворюється та сама частка кількості зовнішньої теплоти:

, Дж/кг, де . (2.42)

При цьому на здійснення зовнішньої механічної роботи приходиться частка теплоти, рівна:

, Дж/кг, (2.43)

де - коефіцієнт розподілу теплоти в політропному процесі.

Теплота, підведена до газу в нескінченно малому політропному процесі, дорівнює:

, Дж/кг (2.44)

чи для кінцевого процесу 1-2: . Таким чином, одержимо теплоємність політропного процесу:, Дж/кгК.

Знаючи значення коефіцієнта в політропному процесі, можна визначити теплоємністьc, теплоту q, зміну внутрішньої енергії і роботу розширення (стиску)l. Для виводу рівняння політропного процесу в p-v координатах використовуємо рівняння першого закону термодинаміки, виражені через энтальпию і внутрішню енергію:

, (2.45)

, (2.46)

чи , (2.47)

. (2.48)

Звідси маємо:

, (2.49)

. (2.50)

Розділивши почленно рівняння (2.49) на рівняння (2.50), маємо:

, (2.51)

де - показник політропного процесу, що не змінюється протягом усього даного ТП. З рівняннямаємо:

, або . (2.52)

Тоді після інтегрування для кінцевої ділянки процесу 1-2 одержимо:

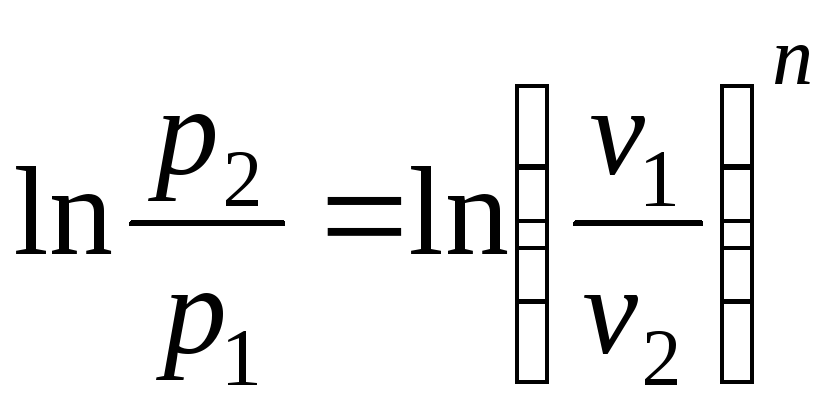, (2.53)

чи після потенціювання: 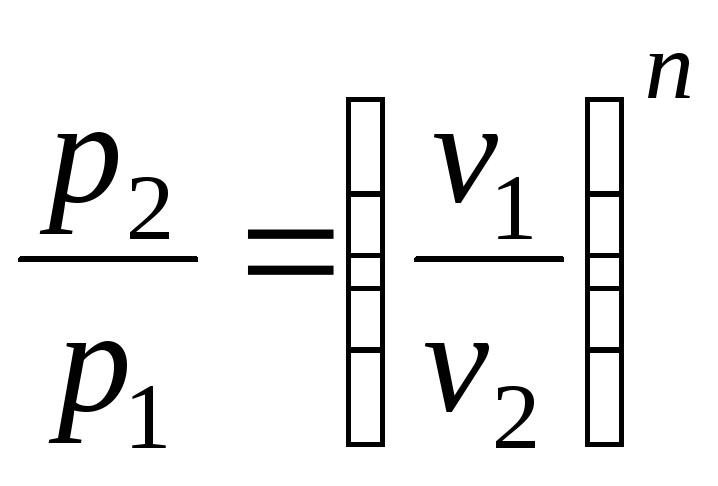, чи. (2.54)

Це рівняння політропного процесу в координатах p-v. Показник політропного процесу може мати будь-яке значення в інтервалі .

В ізохорному процесі теплоємність показник політропи.

В ізобарному процесі теплоємність і показник політропи.

В ізотермному процесі , або, теплоємністьі показник політропи, тобто.

В адіабатному процесі теплоємність і показник політропи.

З виразу можна одержати формулу для розрахунку теплоємності політропного процесу, чи. Звідси маємо, чи, де– показник адіабатного процесу. Остаточно маємо:

. (2.55)

Таким чином, теплоємність політропного процесу залежить від показника політропи . Використовуючи термічне рівняння стану для ідеального газуі рівняння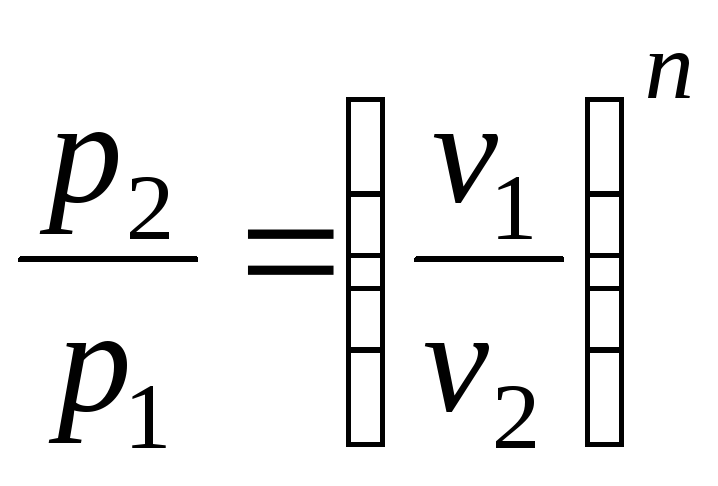, можна одержати співвідношення між параметрами для кінцевого процесу 1-2:

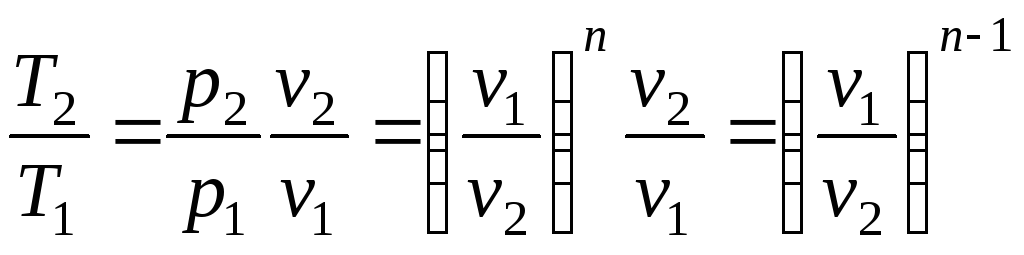. (2.56)

З огляду на те, щ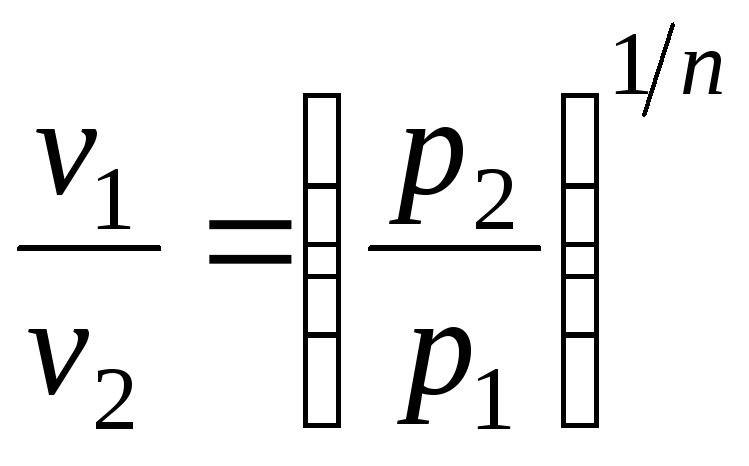о , маємо:

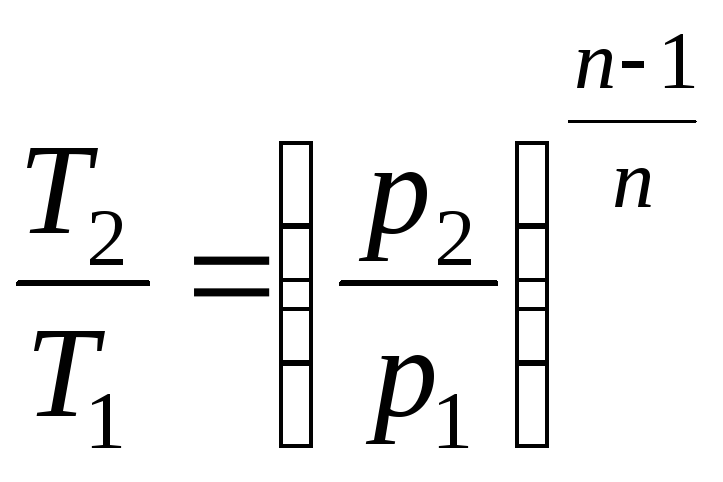. (2.57)

Робота в політропному процесі 1-2 дорівнює:

. (2.58)

Після інтегрування, з огляду на те, що , маємо різні вирази для розрахунку роботи розширення:

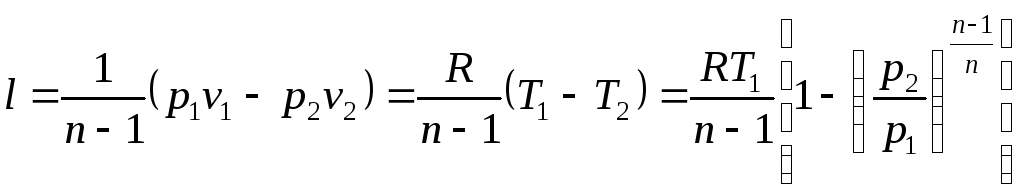. (2.59)

Кількість теплоти згідно першого закону термодинаміки:

. (2.60)

З отримаємо:

, або . (2.61)

Зміна ентропії:

. (2.62)

Оскільки , то коефіцієнт розподілу теплоти дорівнює:

. (2.63)

Тоді зміна внутрішньої енергії, теплота, зміна ентальпії в процесі 1-2 можуть бути розраховані по формулах:

, (2.64)

, (2.65)

. (2.66)

Дослідження політропних процесів. Для того, щоб прослідкувати за розташуванням політропних процесів при різних значеннях , вікоординатах, зображують графіки ізохорного, ізобарного, ізотермногоі адіабатногопоцесів, за якими можна визначити відносне розташування інших політроп при інших значеннях, а також визначити знаків цих процесах (рис. 2.5).

Н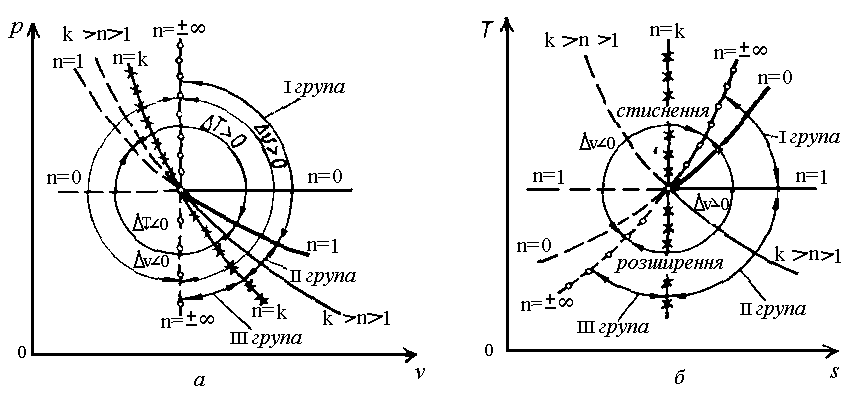априклад, графік політропного процесу зпроходить між графіками процесіві, причому при розширенні в цьому процесі теплота підводиться, оскільки, температура, а отже, внутрішня енергія зменшуються. Робота вцьому випадку здійснюється за рахунок теплоти і зменшення внутрішньої енергії.

Рис. 2.5. Відносне розташування графіків політропного процесу в окремих випадках.

Оскільки знаки теплоти і зміни температури в політропному процесі з показником політропи різні, то теплоємність в цьому випадку буде від’ємною.

В табл. 2.1 наведені особливості трьох груп політропних процесів розширення (процесів, які проходять справа від ізохори).

Таблиця 2.1.