
Шпоры / шпоры тау / 2006дистанционники / Lekcii / Lekcija №21
.doc
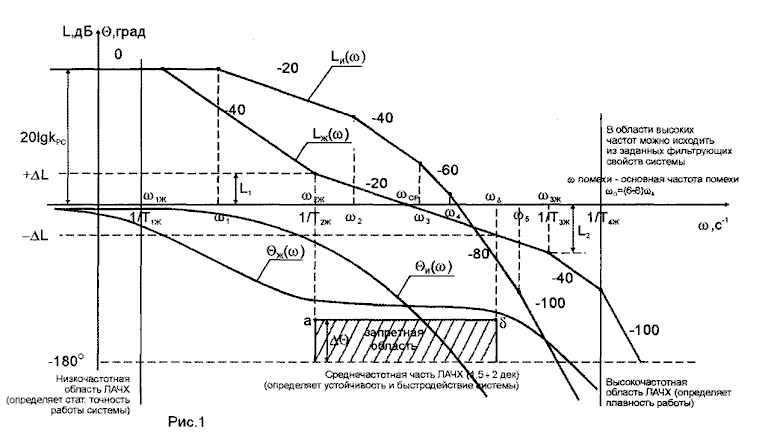
Алгоритм построения желаемых ЛЧХ
-
Выбор частоты среза Lж(w).
Е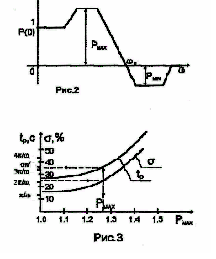 сли
заданы перерегулирование
сли
заданы перерегулирование
![]() и время затухания переходного процесса
и время затухания переходного процесса
![]() ,
то используются номограммы В.В.Солодовникова
или А.В.Фатеева; если задан показатель
колебательности М, то расчет ведут по
методу В.А.Бесекерского.
,
то используются номограммы В.В.Солодовникова
или А.В.Фатеева; если задан показатель
колебательности М, то расчет ведут по
методу В.А.Бесекерского.
В
основу построения номограмм качества
В.В.Солодовниковым положена типовая
вещественная частотная характеристика
замкнутой САУ (рис. 2). Для статических
систем (=0)
![]() ,
для астатических систем (=1,
2,…)
,
для астатических систем (=1,
2,…)
![]() .
.
Этот
метод предполагает, что соблюдается
соотношение
![]() .
.
В
качестве исходных приняты показатели
качества
![]() и
и
![]() ,
которые связаны с параметрами вещественной
частотной характеристики диаграммой
качества (рис. 3). По заданному
,
которые связаны с параметрами вещественной
частотной характеристики диаграммой
качества (рис. 3). По заданному
![]() с помощью кривой
с помощью кривой
![]() (рис.3) определяется соответствующее
значение
(рис.3) определяется соответствующее
значение
![]() .
Затем по
.
Затем по
![]() и кривой
и кривой
![]() определяется значение
определяется значение
![]() ,
которое приравнивается заданному
,
которое приравнивается заданному
![]() ,
получаем
,
получаем
![]()
![]() ,
где
,
где
![]() – значение частоты среза, при котором
время регулирования не превысит заданного
значения
– значение частоты среза, при котором
время регулирования не превысит заданного
значения
![]() .
.
С
другой стороны
![]() ограничивается допустимым ускорением
регулируемой координаты
ограничивается допустимым ускорением
регулируемой координаты
![]() .
Рекомендовано
.
Рекомендовано
![]()
![]() ,
где
,
где
![]() – начальное рассогласование.
– начальное рассогласование.
Время
регулирования
![]() можно приближенно определить, используя
эмпирическую формулу
можно приближенно определить, используя
эмпирическую формулу
![]() ,
где коэффициент числителя принимается
равным 2 при
,
где коэффициент числителя принимается
равным 2 при
![]() ,
3 при
,
3 при
![]() ,
4 при
,
4 при
![]() .
.
Всегда желательно проектирование системы с максимально возможным быстродействием.
Как
правило,
![]() не превышает
не превышает
![]() более, чем на ½ декады. Это связано с
усложнением корректирующих устройств,
необходимостью введения в систему
дифференцирующих звеньев, что уменьшает
надежность и помехоустойчивость, а
также в силу ограничения по максимально
допустимому ускорению регулируемой
координаты.
более, чем на ½ декады. Это связано с
усложнением корректирующих устройств,
необходимостью введения в систему
дифференцирующих звеньев, что уменьшает
надежность и помехоустойчивость, а
также в силу ограничения по максимально
допустимому ускорению регулируемой
координаты.
Частоту
среза
![]() можно повышать лишь увеличением
можно повышать лишь увеличением
![]() .
Статическая точность при этом возрастает,
но ухудшаются условия устойчивости.
.
Статическая точность при этом возрастает,
но ухудшаются условия устойчивости.
Принятие
решения по выбору
![]() должно иметь достаточное обоснование.
должно иметь достаточное обоснование.
-
Строим среднечастотную асимптоту. Ее проводим через точку на оси абсцисс
 с наклоном –20 дБ/дек.
с наклоном –20 дБ/дек. -
Среднечастотную асимптоту сопрягаем с низкочастотной асимптотой
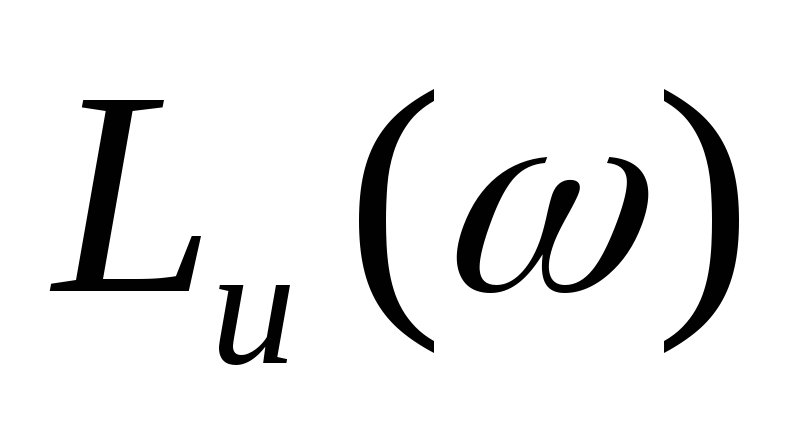 так, чтобы в интервале частот, в котором
так, чтобы в интервале частот, в котором
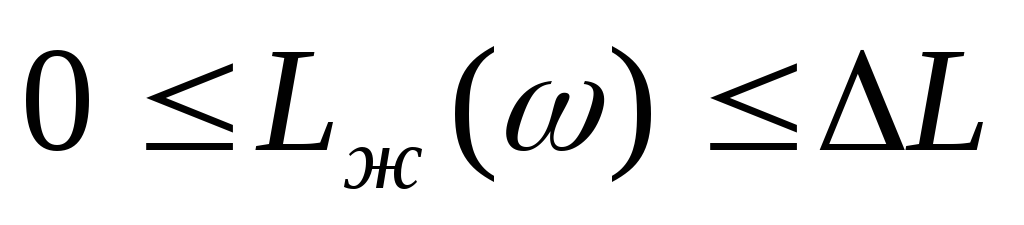 ,
иметь избыток фазы
,
иметь избыток фазы
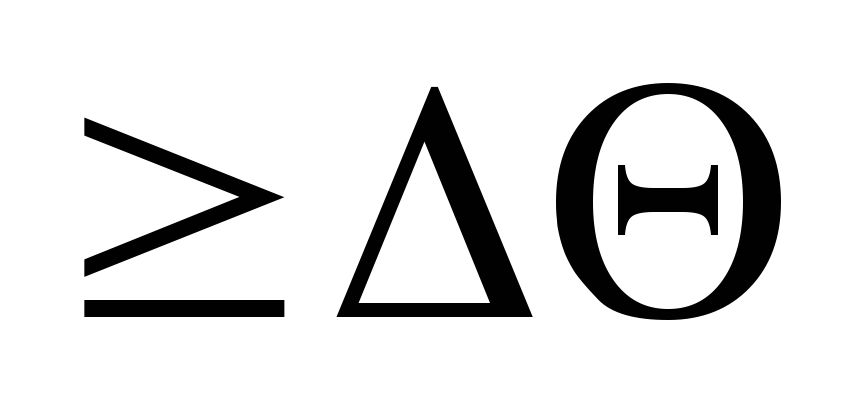 .
Избыток фазы и избыток модуля
.
Избыток фазы и избыток модуля
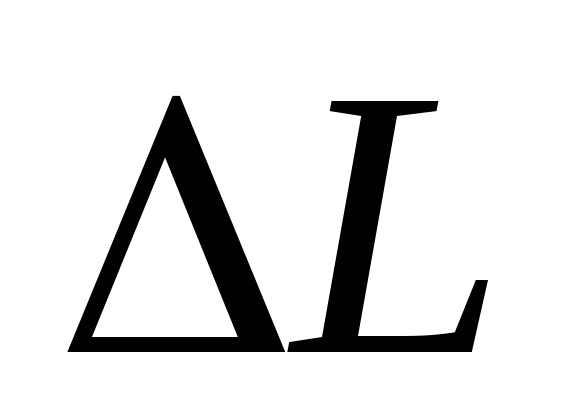 определяем по номограмме (рис. 4).
Сопрягающая асимптота имеет наклон
–20, -40 или –60 дБ/дек при =0
(
- порядок астатизма системы); -40, -60 дБ/дек
при =1
и -60 дБ/дек при =2.
определяем по номограмме (рис. 4).
Сопрягающая асимптота имеет наклон
–20, -40 или –60 дБ/дек при =0
(
- порядок астатизма системы); -40, -60 дБ/дек
при =1
и -60 дБ/дек при =2.
∆L, дБ ∆θ, град
Е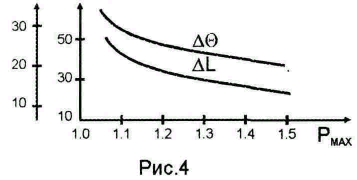 сли
избыток фазы
сли
избыток фазы
![]() окажется меньше
окажется меньше
![]() ,
то сопрягающую асимптоту следует
сместить влево или уменьшить ее наклон.
Если избыток фазы больше допустимого,
то сопрягающую асимптоту смещают вправо
или увеличивают ее наклон.
,
то сопрягающую асимптоту следует
сместить влево или уменьшить ее наклон.
Если избыток фазы больше допустимого,
то сопрягающую асимптоту смещают вправо
или увеличивают ее наклон.
Первоначальная
сопрягающая частота определяется из
выражения
![]() .
.
Рекомендуемая
разность
![]() должна составлять несколько градусов.
Однако, часто (в статических системах)
должна составлять несколько градусов.
Однако, часто (в статических системах)
![]() значительно превосходит
значительно превосходит
![]() ,
и уменьшение
,
и уменьшение
![]() затруднительно. В этом случае принимается
затруднительно. В этом случае принимается
![]() .
.
-
Среднечастотную асимптоту сопрягаем с высокочастотной частью
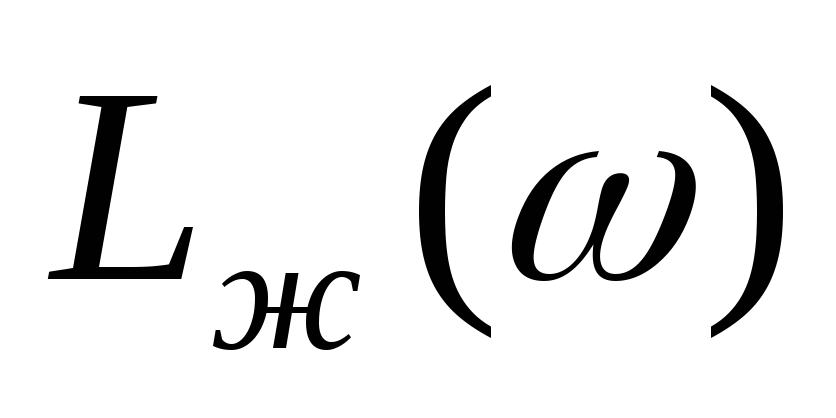 таким образом, чтобы в интервале частот,
где
таким образом, чтобы в интервале частот,
где
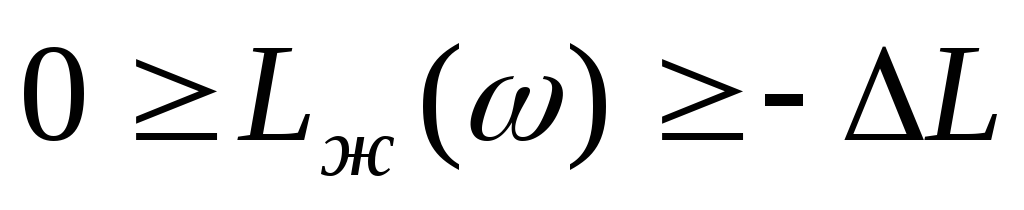 ,
избыток фазы был
,
избыток фазы был
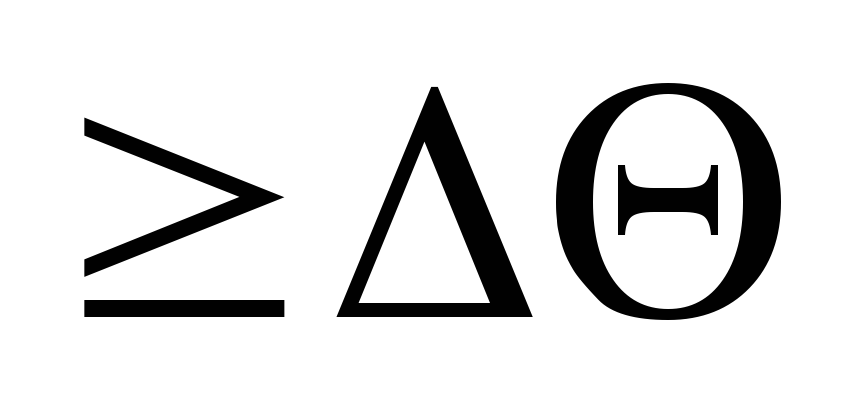 .
Сопрягающую частоту определяем по
соотношению
.
Сопрягающую частоту определяем по
соотношению
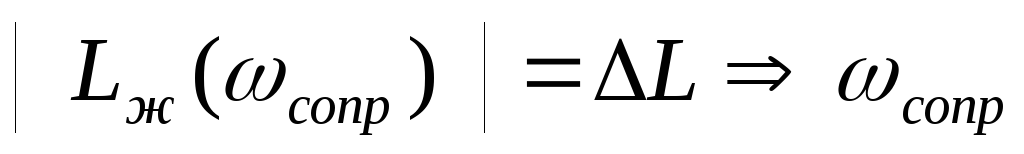 .
.
Если
на сопрягающей частоте
![]() <
<![]() ,
то сопрягающую асимптоту смещают вправо
или уменьшают ее наклон.
,
то сопрягающую асимптоту смещают вправо
или уменьшают ее наклон.
Если
![]() >
>![]() ,
то сопрягающую асимптоту смещают влево
или увеличивают ее наклон. Рекомендуемая
разность
,
то сопрягающую асимптоту смещают влево
или увеличивают ее наклон. Рекомендуемая
разность
![]() должна составлять несколько градусов.
Правая сопрягающая частота сопрягающей
асимптоты
должна составлять несколько градусов.
Правая сопрягающая частота сопрягающей
асимптоты
![]() .
.
Как
правило, наклон этой асимптоты составляет
-40 дБ/дек, а допустимая разность
![]() .
Проверка производится на частоте, при
которой
.
Проверка производится на частоте, при
которой
![]() .
.
-
Высокочастотная часть
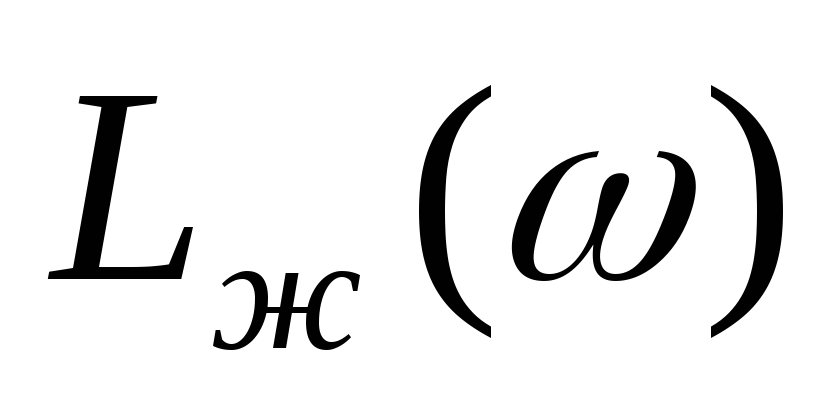 проектируется параллельно
проектируется параллельно
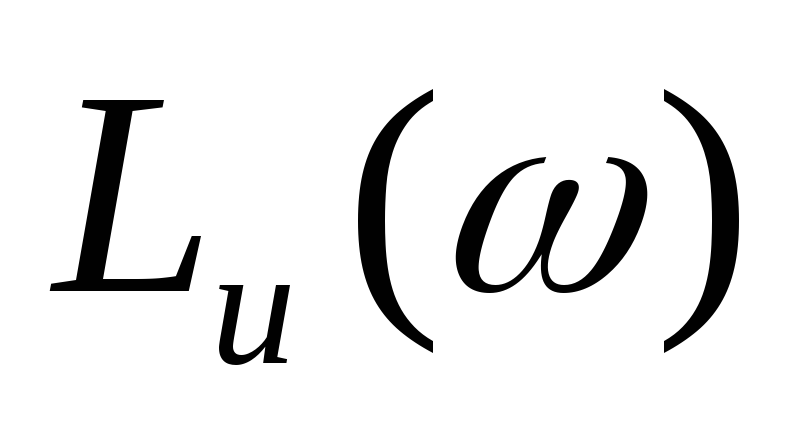 или совмещается с ней. Эта часть
характеристики влияет на плавность
работы системы.
или совмещается с ней. Эта часть
характеристики влияет на плавность
работы системы.
Итак,
на первом этапе построения
![]() частоты, на которых сопрягается
среднечастотная асимптота с сопрягающими
асимптотами, находятся из условий
частоты, на которых сопрягается
среднечастотная асимптота с сопрягающими
асимптотами, находятся из условий
![]() .
На втором этапе уточняются значения
сопрягающих частот с учетом избытков
фазы. На третьем этапе корректируются
все сопрягающие частоты
.
На втором этапе уточняются значения
сопрягающих частот с учетом избытков
фазы. На третьем этапе корректируются
все сопрягающие частоты
![]() по условию их близости к сопрягающей
частоте исходной системы, т. е.
по условию их близости к сопрягающей
частоте исходной системы, т. е.
![]() ,
если эти частоты незначимо отличаются
друг от друга.
,
если эти частоты незначимо отличаются
друг от друга.
Синтез корректирующей цепи последовательного типа
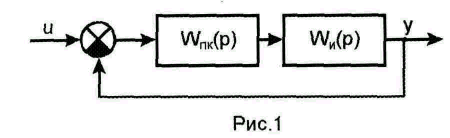
В
схеме рис.1
![]() ,
отсюда могут быть получены параметры
корректирующей цепи:
,
отсюда могут быть получены параметры
корректирующей цепи:
![]() .
.
Перейдем
к логарифмическим частотным характеристикам:
![]() ,
,
![]() .
.
Рассмотрим на примере расчет последовательной корректирующей цепи.
Пусть
требуется скорректировать статическую
систему. Предположим, что
![]() и
и
![]() нами построены. Полагаем, что система
с минимально-фазовыми звеньями, поэтому
фазо-частотную характеристику не строим
(рис.2).
нами построены. Полагаем, что система
с минимально-фазовыми звеньями, поэтому
фазо-частотную характеристику не строим
(рис.2).
![]() ,
,
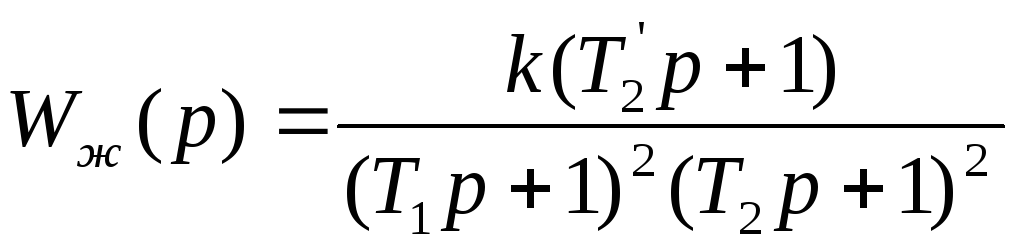 ,
,
![]() .
.
Т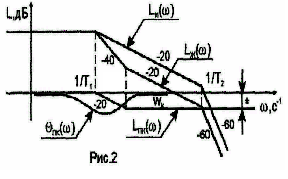 еперь
легко воспроизвести параметры
корректирующей цепи. Чаще всего
используются активные корректирующие
устройства и пассивные RC-цепи.
Исходя из физических представлений
строим цепь, изображенную на рис. 3.
еперь
легко воспроизвести параметры
корректирующей цепи. Чаще всего
используются активные корректирующие
устройства и пассивные RC-цепи.
Исходя из физических представлений
строим цепь, изображенную на рис. 3.
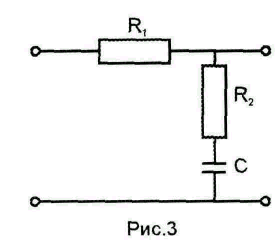 Ослаблению
сигнала делителем R1-R2
на высоких частотах соответствует
ослабление сигнала * на
Ослаблению
сигнала делителем R1-R2
на высоких частотах соответствует
ослабление сигнала * на
![]() .
.
![]() ,
где
,
где
![]() ,
,
![]() .
.
![]() на высоких частотах
не вносит искажений – положительный
фактор. Частоту среза имеем возможность
сдвинуть влево с помощью корректирующей
цепи и обеспечить требуемые устойчивость
и качество работы системы.
на высоких частотах
не вносит искажений – положительный
фактор. Частоту среза имеем возможность
сдвинуть влево с помощью корректирующей
цепи и обеспечить требуемые устойчивость
и качество работы системы.
Достоинства последовательных КУ:
-
Простота корректирующего устройства (во многих случаях реализуются в виде простых пассивных RC-контуров);
-
Простота включения.
Недостатки:
-
Эффект последовательной коррекции уменьшается в процессе эксплуатации при изменении параметров (коэффициентов усиления, постоянных времени), поэтому при последовательной коррекции к стабильности параметров элементов предъявляются повышенные требования, что достигается применением более дорогостоящих элементов;
-
Дифференцирующие фазоопережающие RC-контуры чувствительны к высокочастотным помехам;
-
Последовательные интегрирующие RC-контуры содержат более громоздкие конденсаторы, чем контуры в цепи обратной связи.
Применяются обычно в маломощных системах. Это объясняется, с одной стороны, простотой последовательных корректирующих устройств, а с другой стороны, нецелесообразностью применения в этих системах громоздких, соизмеримых с размерами исполнительного двигателя таких параллельных корректирующих устройств, как тахогенератор.
Следует
иметь в виду, что из-за насыщения
усилителей не всегда целесообразно
осуществлять формирование желаемой
ЛАЧХ в диапазоне низких и средних частот
за счет последовательного включения в
систему интегрирующих и интегродифференцирующих
цепей или каких-нибудь других элементов
с аналогичными характеристиками. Поэтому
часто для формирования
![]() в диапазоне низких и средних частот
применяются обратные связи.
в диапазоне низких и средних частот
применяются обратные связи.
