3.5.3. Фундаментальное множество циклов

Каркас (V,T) связного неориентированного графа G=<V,E> содержит N-1 ребро, где N - количество вершин G. Каждое ребро, не принадлежащее T, то есть любое ребро из E-T, порождает в точности один цикл при добавлении его к T. Такой цикл является элементом фундаментального множества циклов графа G относительно каркаса T. Поскольку каркас состоит из N-1 ребра, в фундаментальном множестве циклов графа G относительно любого каркаса имеется M-N+1 циклов, где M - количество ребер в G.

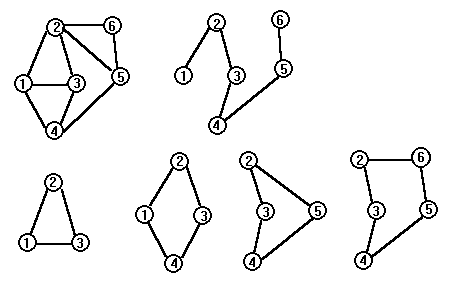Пример графа, его каркаса и множества фундаменталь-ных циклов.

Поиск в глубину является естественным подходом, используемым для нахождения фундаментальных циклов. Строится каркас, а каждое обратное ребро порождает цикл относительно этого каркаса. Для вывода циклов необходимо хранить порядок обхода графа при поиске в глубину (номера вершин) - массив St, а для определения обратных ребер вершины следует “метить” (массив Gnum) в той очередности, в которой они просматриваются. Если для ребра <v,j> оказывается, что значение метки вершины с номером j меньше, чем значение метки вершины с номером v, то ребро обратное и найден цикл.

Начальная инициализация переменных.

......

num:=0;yk:=0;

for j:=1 to N do Gnum[j]:=0;

.......

Логика.

procedure Circl(v:integer);

{глобальные переменные: А - матрица смежности графа; St - массив для хранения номеров вершин графа в том порядке, в котором они используются при построении каркаса; yk - указатель записи в массив St; Gnum - для каждой вершины в соответствующем элементе массива фиксируется номер шага (num), на котором она просматривается при поиске в глубину}

var j:integer;

begin

Inc(yk);St[yk]:=v;Inc(num);

Gnum[v]:=num;

for j:=1 to N do if A[v,j]<>0 then

if Gnum[j]=0 then Circl[j] {вершина j не просмотрена}

{j не предыдущая вершина при просмотре, и она была просмотрена ранее}

else if (j<>St[yk-1]) and (Gnum[j]<Gnum[v]) then

<вывод цикла из St>;

Dec(yk);

end;

Дополнения.

Название “фундаментальный” связано с тем, что каждый цикл графа может быть получен из циклов этого множества. Для произвольных множеств A и B определим операцию симметрической разности AÅB=(AÈB)\(AÇB). Известно [9], что произвольный цикл графа G можно однозначно представить как симметрическую разность некоторого числа фундаментальных циклов. Однако не при всех операциях симметрической разности получаются циклы (вырожденный случай). Исследовательская работа - разработать программу нахождения всех циклов графа.

3.6. Кратчайшие пути

3.6.1. Постановка задачи. Вывод пути

Постановка задачи. Дан ориентированный граф G=<V,E>, веса дуг - А[i,j] (i,j=1..N, где N - количество вершин графа), начальная и конечная вершины - s, tÎV. Веса дуг записаны в матрице смежности A, если вершины i и j не связаны дугой, то A[i,j]=¥. Путь между s и t оцениваетсяåA[i,j]. Найти путь с минимальной оценкой. i,jÎпути

Пример.

Кратчайший путь из 1 в 4 проходит через 3-ю и 2-ю вершины и имеет оценку 6.

Особый случай - контуры с отрицательной оценкой.

Пример.

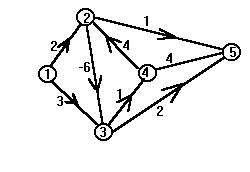При s=1 и t=5, обходя контур 3®4®2®3 достаточное число раз, можно сделать так, что оценка пути между вершинами 1 и 5 будет меньше любого целого числа. Оценку пути назовем его весом или длиной. Будем рассматривать только графы без контуров отрицательного веса.

Нам необходимо найти кратчайший путь, то есть путь с минимальным весом, между двумя вершинами графа. Эта задача разбивается на две подзадачи: сам путь и значение минимального веса . Обозначим ее через D[s,t]. Неизвестны алгоритмы, определяющие только D[s,t], все они определяют оценки от вершины s до всех остальных вершин графа. Определим D, как array[1..n] of integer. Предположим, что мы определили значения элементов массива D - решили вторую подзадачу. Определим сам кратчайший путь. Для s и t существует такая вершина v, что D[t]=D[v]+A[v,t]. Запомним v (например, в стеке) . Повторим процесс поиска вершины u, такой, что D[v]=D[u]+A[u,v], и так до тех пор, пока не дойдем до вершины с номером s. Последовательность t, v, u, ..., s дает кратчайший путь.

procedure Way(s,t:integer);

{D, A - глобальные структуры данных}

var v,u:integer;

Stack - локальная структура данных для хранения номеров вершин;

procedure Print;

{выводит содержимое Stack}

begin

...

end;

begin

<почиститьStack>;

<занести вершину с номером t в Stack>;v:=t;

while v<>s do begin

u:=<номер вершины, для которой D[v]=D[u]+A[u,v]>;

<занести вершину с номеромvв Stack>;

v:=u;

end;

end;

Итак, путь при известном D находить мы умеем. Осталось научиться определять значения кратчайших путей, то есть элементы массива D. Идея всех известных алгоритмов заключается в следующем. По данной матрице весов A вычисляются первоначальные верхние оценки. А затем пытаются их улучшить до тех пор, пока это возможно. Поиск улучшения, например для D[v], заключается в нахождении вершин u, таких, что D[u]+A[u,v]<D[v]. Если такая вершина u есть, то значение D[v] можно заменить на D[u]+A[u,v].