3.4.2. Определение связности
Определения. Неориентированный граф G связен, если существует хотя бы один путь в G между каждой парой вершин i и j. Ориентированный граф G связен, если неориентированный граф, получающийся из G путем удаления ориентации ребер, является связным. Ориентированный граф сильно связен, если для каждой пары вершин i и j существует по крайней мере один ориентированный путь из i в j и по крайней мере один из j в i. Максимальный связный подграф графа G называется связной компонентой графа G. Максимальный сильно связный подграф называется сильно связной компонентой.
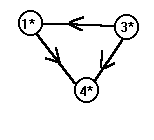Рассмотрим
алгоритм нахождения сильных компонент
графа. Идея достаточна проста. Для
вышеприведенного примера значение
R(1)={1}È{2,5}È{6}È{4}È{7}={1,2,4,5,6,7},
а Q(1)={1}È{2,5}È{3}.
Пересечение этих множеств дает множество
C(1)={1,2,5} вершин графа G, образующих сильную
компоненту, которой принадлежит вершина
графа с номером 1. Продолжим рассмотрение:
R(3)={1,2,3,4,5,6,7}, Q(3)={3} и C(3)={3}; R(4)={4}È{7}È{6}={4,6,7}
и Q(4)={4}È{6}È{7}={4,6,7}
и С(4)={4,6,7}. Итак, мы нашли сильные компоненты
графа G. Граф G*=(V*,E*) определим так: каждая
его вершина представляет множество
вершин некоторой сильной компоненты
графа G, дуга (i*, j*) cуществует в G* тогда
и только тогда, когда в G существует
дуга (i,j), такая, что i принадлежит
компоненте, соответствующей вершине
i*, а j - компоненте, соответствующей
вершине j*. Граф G* называется конденсацией
графа G.
Дополнения.
1. Доказать, что в конденсации графа не содержится циклов.
2. Доказать, что в ориентированном графе каждая вершина i может принадлежать только одной сильной компоненте.
3. В графе есть множество вершин P, из которых достижима любая вершина графа и которое является минимальным в том смысле, что не существует подмножества в P, обладающего таким свойством достижимости. Это множество вершин называется базой графа. Показать, что в P нет двух вершин, которые принадлежат одной и той же сильной компоненте графа G.
Показать, что любые две базы графа G имеют одно и то же число вершин.
Разработать программу нахождения базы графа. Схема решения. База P* конденсации G* графа G состоит из таких вершин графа G*, в которые не заходят ребра. Следовательно, базы графа G можно строить так: из каждой сильной компоненты графа G, соответствующей вершине базы P* конденсации G*, надо взять по одной вершине - это и будет базой графа G.
3.4.3. Двусвязность
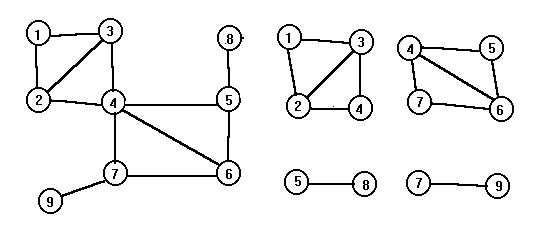
Иногда недостаточно знать, что граф связен. Может возникнуть вопрос, насколько “сильно связен” связный граф. Например, в графе может существовать вершина, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся вершины. Такая вершина называется точкой сочленения, или разделяющей вершиной. Граф, содержащий точку сочленения, называется разделимым. Граф без точек сочленения называется двусвязным или неразделимым. Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Пример.Разделимый граф и его двусвязные компоненты. Точки сочленения вершины с номерами 4, 5 и 7.
Точку
сочленения можно определить иначе.
Вершина t является точкой сочленения,
если существуют вершины u и v, отличные
от t, такие, что каждый путь из u в v
(предполагаем, что существует по крайней
мере один) проходит через вершину с
номером t.
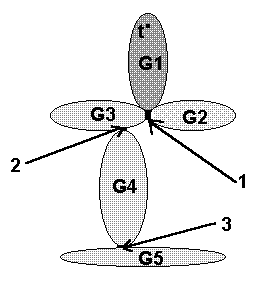Наша
задача - найти точки сочленения и
двусвязные компоненты графа. Основная
идея. Есть двусвязные компоненты G1, G2,
G3, G4 и G5 и точки сочленения 1, 2, 3. Осуществляем
поиск в глубину из вершины t, принадлежащей
G1. Мы можем перейти из G1 в G2, проходя
через вершину 1. Но по свойству поиска
в глубину все ребра G2 должны быть пройдены
до того, как мы вернемся в 1. Поэтому G2
состоит в точности из ребер, которые
проходятся между заходами в вершину 1.
Для других чуть сложнее. Из G1 попадаем
в G3, затем в G4 и G5. Предысторию процесса
прохождения ребер будем хранить в стеке.
Тогда при возвращении в G4 из G5 через
вершину 3 все ребра G5 будут на верху
стека. После их удаления, то есть вывода
двусвязной компоненты из стека, на верху
стека будут ребра G4, и в момент прохождения
вершины 2 мы можем их опять вывести.
Таким образом, если распознать точки
сочленения, то, применяя поиск в глубину
и храня ребра в стеке в той очередности,
в какой они проходятся, можно определить
двусвязные компоненты. Ребра, находящиеся
на верху стека в момент обратного прохода
через точку сочленения, образуют
двусвязную компоненту.
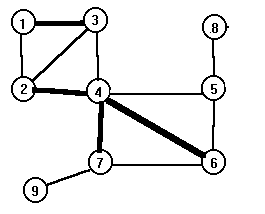Итак,
проблема с точками сочленения. Рассмотрим
граф. В процессе просмотра в глубину
все ребра разбиваются на те, которые
составляют дерево (каркас), и множество
обратных ребер. Обратные ребра выделены
на рисунке более жирными линиями.
Что нам это дает? Пусть очередность просмотра вершин в процессе поиска в глубину фиксируется метками в массиве Num. Для нашего примера Num - (1,2,3,4,5,6,7,9,8). Если мы рассматриваем обратное ребро (v,u), и v не предок u, то информацию о том, что Num[v] больше Num[u], можно использовать для пометки вершин v и u как вершин, принадлежащих одной компоненте двусвязности. Массив Num использовать для этих целей нельзя, поэтому введем другой массив Lowpg и постараемся пометить вершины графа, принадлежащие одной компоненте двусвязности одним значением метки в этом массиве. Первоначальное значение метки совпадает со значением соответствующего элемента массива Num. При нахождении обратного ребра (v,u) естественной выглядит операция: Lowpg[v]:=Min(Lowpg[v],Num[u]) - изменения значения метки вершины v, так как вершины v и u из одной компоненты двусвязности. К этой логике необходимо добавить смену значения метки у вершины v ребра (v,u) на выходе из просмотра в глубину в том случае, если значение метки вершины u меньше, чем метка вершины v (Lowpg[v]:= Min(Lowpg[v],Lowpg[u])). Для нашего примера массив меток Lowpg имеет вид: (1,1,1,2,4,4,4,9,8). Осталось определить момент вывода компоненты двусвязности. Мы рассматриваем ребро (v,u), и оказывается, что значение Lowpg[u] больше или равно значению Num[v]. Это говорит о том, что при просмотре в глубину между вершинами v и u не было обратных ребер. Вершинаv- точка сочленения, и необходимо вывести очередную компоненту двусвязности, начинающуюся с вершиныv.
Итак, логика.
procedure Dvy(v,p:integer);{вершина p - предок вершины v}
{массивы A, Num, Lowpg и переменная nm - глобальные}
var u:integer;
begin
Inc(nm);Num[v]:=nm;Lowpg[v]:=Num[v];
for u:=1 to N do
if A[v,u]<>0 then if Num[u]=0 then begin
<сохранить ребро (v,u) в стеке>;
Dvy(u,v);
Lowpg[v]:=Min(Lowpg[v],Lowpg[u]);
{функция, определяющая минимальное из двух чисел }
if Lowpg[u]>=Num[v] then <вывод компоненты>;
end
else if (u<>p) and (Num[v]>Num[u]) then begin
{u не совпадает с предком вершины v}
<сохранить ребро (v,u) в стеке>;
Lowpg[v]:=Min(Lowpg[v],Num[u]);
end;
end;
Фрагмент основной логики:
....
FillChar(Num,SizeOf(Num),0);
FillChar(Lowpg,SizeOf(Lowpg),0);
nm:=0;
for v:=1 to N do if Num[v]=0 then Dvy(v,0);
....
Дополнение. Мостом графа G называется каждое ребро, удаление которого приводит к увеличению числа связных компонент графа. Разработать программу нахождения всех мостов графа. Покажите, что мосты графа должны быть в каждом каркасе графа G. Каким образом знание мостов графа может изменить (ускорить) логику нахождения всех его каркасов?