2.10.3. Алгоритм Кристофидеса

Отличается от предыдущего логикой построения маршрута из каркаса минимального веса. Неравенство треугольника выполняется.

Шаг 1. Строится каркас минимального веса (алгоритм Прима или Краскала).

Шаг 2. На множестве вершин каркаса(обозначим их через V), имеющих нечетное число ребер каркаса, находится паросочетание минимального веса. Таких вершин в любом каркасе четное число. Метод поиска паросочетания - чередующиеся цепочки.

Шаг 3. Каркас преобразуется в эйлеров граф путем присоединения ребер, соответствующих найденному паросочетанию.

Шаг 4. В построенном графе находится эйлеров маршрут.

Шаг 5. Эйлеров маршрут преобразуется в маршрут коммивояжера:

Итак, данный метод отличается от предыдущего только шагами 2 и 3.

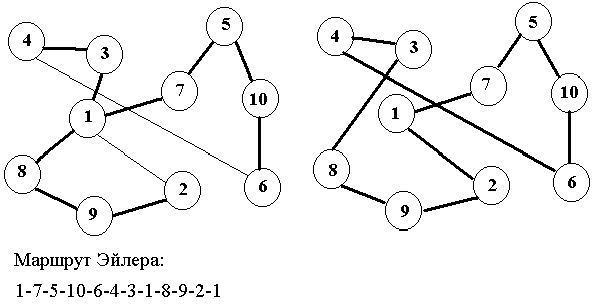
Все этапы реализуются за полиномиальное время. Известно[1], что для этого метода оценка приближенного метода имеет видCostAp<1.5*CostBestи эта оценка является лучшей для приближенных полиномиальных алгоритмов решения задачи о коммивояжере с неравенством треугольника. На данных из п. 2.1.7 на рисунке показан пример каркаса (жирными линиями) и паросочетание минимального веса (тонкими линиями), построенное на вершинах каркаса с нечетными степенями. Путь коммивояжера имеет стоимостьCostAp, равную 191, что составляет~ 1.2*CostBest.

В логикуsolve (см. предыдущий алгоритм) добавляется процедура построения паросочетания минимального веса (P). Назовем ееpair.Ее входными данными является матрицаB(описывает каркас), выходными - новая матрица С (элементы логического типа), соответствующая графу получаемому добавлением к каркасу реберP.

Procedure pair;

var ?;

<процедурыpair>;

begin

init_pair;{инициализация переменных процедуры, формирование массива с номерами вершин, имеющих нечетную степень}

first;{поиск первого паросочетания}

find;{поискP}

ad;{добавление ребер, образующихPк каркасу - матрица С}

end;

Примечание. Возможен вариант уточнения логики до работающей программы (это уже теоретическое занятие, которые мы очень не любим). Однако перед этим занятием школьники повторяют ранее изученные алгоритмы построения паросочетаний в графе, так что на этой стадии детализации можно и остановиться.

3.11. Задачи

1. Дан ориентированный граф с N вершинами (N<50).Вершины и дуги окрашены в цвета с номерами от 1 доM (M£6).Указаны две вершины, в которых находятся фишки игрока и конечная вершина. Правило перемещения фишек: игрок может передвигать фишку по дуге, если ее цвет совпадает с цветом вершины, в которой находится другая фишка; ходы можно делать только в направлении дуг графа; поочередность ходов необязательна. Игра заканчивается если одна из фишек достигает конечной вершины.

Написать программу поиска кратчайшего пути до конечной вершины, если он существует.

2. Некоторые школы связаны компьютерной сетью. Между школами заключены соглашения: каждая школа имеет список школ-получателей, которым она рассылает программное обеспечение всякий раз, получив новое бесплатное программное обеспечение (извне сети или из другой школы). При этом, если школа В есть в списке получателей школы А, то школа А может не быть в списке получателей школы В.

Требуется написать программу, определяющую минимальное количество школ, которым надо передать по экземпляру нового программного обеспечения, чтобы распространить его по всем школам сети в соответствии с соглашениями.

Кроме того, надо обеспечить возможность рассылки нового программного обеспечения из любой школы по всем остальным школам. Для этого можно расширять списки получателей некоторых школ, добавляя в них новые школы. Требуется найти минимальное суммарное количество расширений списков, при которых программное обеспечение из любой школы достигло бы всех остальных школ. Одно расширение означает добавление одной новой школы-получателя в список получателей одной из школ.

3. Задан неориентированный граф. При прохождении по некоторым ребрам некоторые (определенные заранее) ребра могут исчезать или появляться.

Найти кратчайший путь из вершины с номером qв вершину с номеромw.

4. Заданы два числа N иM(20£M£N£150),гдеN -количество точек на плоскости. Требуется построить дерево изMточек так, чтобы оно было оптимальным. Дерево называется оптимальным, если сумма всех его ребер минимальна. Все ребра - это расстояния между вершинами, заданными координатами точек на плоскости.

5. Даны два числаN иM.Построить граф изN вершин иMребер. Каждой вершине ставится в соответствие число ребер, входящих в нее. Граф должен быть таким, чтобы сумма квадратов этих чисел была минимальна.

6. Задан ориентированный граф с Nвершинами, каждому ребру которого приписан неотрицательный вес. Требуется найти простой цикл, для которого среднее геометрическое весов его ребер было бы минимально.

Примечание. Цикл называется простым, если через каждую вершину он проходит не более одного раза, петли в графе отсутствуют.

7. Компьютерная сеть состоит из связанных между собой двусторонними каналами связиNкомпьютеров (N не превосходит 50, а количество каналовN+5), номера которых от 1 доN.Эта сеть предназначена для распространения сообщения от центрального компьютера всем остальным. Компьютер, получивший сообщение, владеет им и может распространять его дальше по сети. Запрещается передавать сообщения одному и тому же компьютеру дважды. Время передачи сообщения по каналу связи занимает одну секунду, при этом передающий и принимающий компьютеры заняты на все время передачи данного сообщения. На рисунке приведен возможный вариант такой сети.

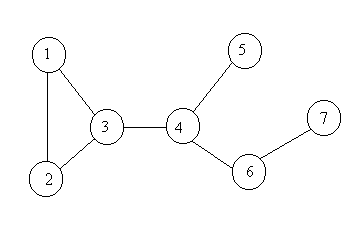
В начальный момент времени центральный компьютер может передать сообщение одному из непосредственно связанных с ним компьютеров, т.е. соседу. После окончания передачи, этим сообщением будут владеть оба компьютера. Каждый из них может передать сообщение одному из своих соседей и так далее, пока все компьютеры не будут владеть сообщением. Для сети, показанной на рисунке, возможный порядок распространения сообщения от центрального компьютера с номером 6 имеет вид:

Секунда 1: 6®4

Секунда 2: 4®3

6®7

Секунда 3: 3®1

4®5

Секунда 4: 3®2

Написать программу определения и вывода порядка передачи сообщения за минимальное время.

8. Внутрь квадрата с координатами левого нижнего угла (0,0) и координатами верхнего угла (100, 100) поместилиN (1£N£30) квадратиков. Необходимо найти кратчайший путь из точки (0,0) в точку (100,100), который бы не пересекал ни одного из этих квадратиков. Ограничения:

• длина стороны каждого квадратика равна 5;

• стороны квадратиков параллельны осям координат;

• координаты всех углов квадратиков - целочисленные;

• квадратики не имеют общих точек.

  9. Задан неориентированный граф с Nвершинами, пронумерованными целыми числами от 1 доN. Написать программу, которая последовательно решает следующие задачи:

• выясняет количество компонент связности графа;

• находит и выдает все такие ребра, что удаление любого из них ведет к увеличению числа компонент связности;

• определяет, можно ли ориентировать все ребра графа таким образом, чтобы получившийся граф оказался сильно связным;

• ориентирует максимальное количество ребер, чтобы получившийся граф оказался сильно связным;

• определяет минимальное количество ребер, которые следует добавить в граф, чтобы ответ на третий пункт был утвердительным.

  10. Задан ориентированный граф с N (1£N£33) вершинами, пронумерованными целыми числами от 1 доN. Напишите программу, которая подсчитывает количество различных путей между всеми парами вершин графа.

  11. Ребенок нарисовал кружки и некоторые из них соединил отрезками. Кружки он пометил целыми числами от 1 до N (1£N£30), а на каждом отрезке поставил стрелочку. Затем он приписал каждому кружочку вес в виде некоторого целого числа и определил начальный и конечный кружочки. Из первого он должен выйти, а во второй попасть.

  Ребенок решил для себя следующее:

• набрать максимально возможное суммарное количество очков;

• по каждому отрезку пройти ровно один раз;

• если в кружок он попадает при движении по направлению стрелки, то к суммарному количеству очков вес этого кружка прибавляется;

• если в кружок он попадает при движении против направления стрелки, то из суммарного количества очков вес этого кружка вычитается.

Написать программу, которая бы помогла ребенку построить путь, удовлетворяющий всем этим требованиям.

Литература

1. Адельсон-Вельский Г.М., Диниц Е.А., Карзанов А.В. Потоковые алгоритмы.-М.:Наука,1975.

2. Берж К. Теория графов и ее применение. - М.: ИЛ, 1962.

3. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. - М.: Наука, 1990.

4. Зыков А. А. Теория конечных графов.-Новосибирск:Наука; Сиб. отд-ние, 1969.

5. Йенсен П., Барнес Д. Потоковое программирование.-М.:Радио и связь,1984.

6. Касьянов В.Н., Сабельфельд В.К. Сборник заданий по практикуму на ЭВМ. - М.: Наука, 1986.

7. Кристофидес Н. Теория графов. Алгоритмический подход.-М.: Мир, 1978.

8. Кофман А. Введение в прикладную комбинаторику.-М.:Наука,1975.

9. Липский В. Комбинаторика для программистов.-М.:Мир, 1988.

10. Майника Э. Алгоритмы оптимизации на сетях и графах.-М.:Мир,1981.

11. Нечепуренко М.И., Попков В.К., Майнагашев С.М. и др. Алгоритмы и программы решения задач на графах и сетях.-Новосибирск: Наука; Сиб. отд-ние, 1990.

12. Окулов С.М.Конспекты занятий по информатике (алгоритмы на графах). Учебное пособие для студентов и учителей школ. - Киров, 1996.

13. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация: Алгоритмы и сложность.-М.:Мир,1985.

14. Свами М., Тхуласираман К. Графы, сети и алгоритмы.- М.:Мир,1984.

15. Филипс Д., Гарсиа-Диас А. Методы анализа сетей. - М.: Мир, 1984.

16. Форд Л.Р., Фалкерсон Д.Р. Потоки в сетях.-М.:Мир,1963.

17. Фрэнк Г., Фриш И. Сети, связь и потоки.-М.:Связь,1978.

18. Харари Ф. Теория графов.-М.:Мир,1973.

19. Ху Т. Целочисленное программирование и потоки в сетях.- М.:Мир,1974.

148