Свойства реляционных операций.
Для наглядности будем использовать базу Поставщик – Деталь – Поставка.
Поставщик (код_поставщика, фамилия, статус, город);
Деталь (код_детали, название, вес, цвет, город);
Поставка ( код_детали, код_поставщика, количество).
Операция селекции.
Запрос: получить информацию о поставщиках из Перми.
Эта информация находится в таблице Поставщики, из этой таблицы нужно отобрать строки, в которых город=Пермь.
Отобразить информацию о поставщиках из Перми, статус которых >50.
,
при этом порядок селекций произвольный,
т.е. операция
селекция коммутативна относительно
суперпозиции селекции:
-можно
записывать так.
Пусть нужно найти информацию о поставщиках из города Перми или тех у кого статус больше 50.
В данном случае будем использовать объединение селекций:
.
Операция селекции дистрибутивна относительно операций объединения, разности и пересечения:
Вопрос:
если дано r(A,B,C)
, то на запрос
,
ответ будет состоять из одной записи,
так как ключ является уникальной записью.
Операция проекции.
Запрос: необходимо получить номера поставляемых деталей.
Так как в запросе присутствует отглагольная форма, то требуемую информацию необходимо искать в связующей таблице, т.е. в таблице Поставки.
Свойства операции проекции:
Если
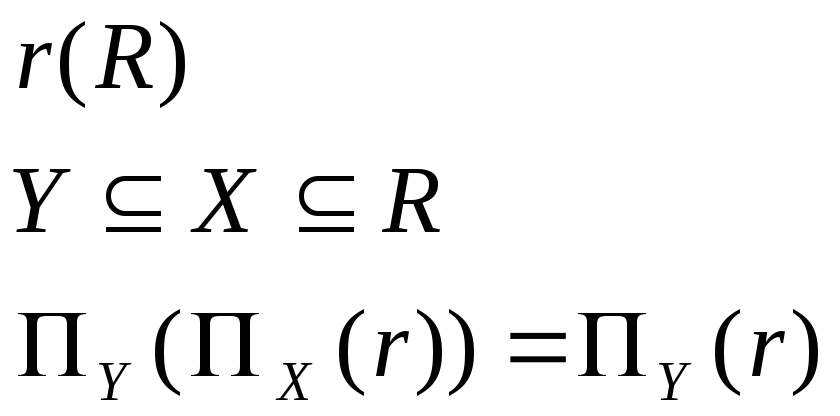,то
То есть операция проекции дает результат самого внешнего атрибута, если он является подмножеством.
Запишем законы дистрибутивности проекции по отношению к операциям пересечения, разности и объединения:
;
;
.
Докажем на примерах второе и третье соотношение.
а) дано r(A,B) s(A,B)
ab1 a2b
ab a2b1
a1b
a1b2
пересечение дает
пустое множество r
s=0,
а если сначала найти проекции
и
,
то ответ будет иным:
=(B)
=(B)
b b
b1 b1
b2
тогда
=(B)
b
b1
0
б) Дано r(A,B) s(A,B)
ab1 a2b
ab a2b1
a1b
a1b2
Операция разности дает следующий результат: r\s=(A,B)
ab1
ab
a1b
a1b2,
а
проекция от разности равна:
b1
b
b2,
а если сначала найти проекции, а потом их разность, то получим следующий результат:
b1 b
b b1
b2
b2
Еще одно свойство:
,
при этом в
должны использоваться те атрибуты,
которые принадлежат X.
Операция соединения.
С помощью операции соединения можно выполнить операцию селекции, при этом операция селекции равносильна квантору существования.
Е
сли
дано r(R), и необходимо выполнить операцию
селекции
,
то ее можно выполнить с помощью операции
соединения r s(A)
Пример
Запрос: существует ли поставщик из Березников со статусом 80?
(Поставщик
s(город, статус))
Березники, 80
Операция соединения коммутативна:
r
s = s r
Операция соединения ассоциативна:
r
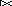1
(r2 r3)=(r1 r2) r3
Операция соединения дистрибутивна относительно операций пересечения, объединения и разности:
(
r1
r2)
s = (r1
s)
(r2
s);
(
r1
r2)
s = (r1
s)
(r2
s);
(
r1\r2)
s = (r1\s) (r2\s)/
Свойство идемпотентности:
q
q=q;
q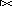
r = q (q r )
Свойство полусоединения:
(r
s) =
(r)
s
Условие полного соединения
Д
ано
r(R) и s(S), тогда q(RS)=r s
,
если выполняется равенство, то r полностью
соединимо.
,
если выполняется равенство, то s полностью
соединимо.
Пример:
r(A,B) s(A,B) q(A,B,C)
ab1 b1c ab1c
ab2
A,B
ab – неполное соединение
B,C
b1c - полное соединение.
Для того чтобы было полное соединение необходимо, чтобы в соединяемых столбцах были все значения R и S.
Условие разложения без потерь.
q(R,S)
r=
s=
r
s=
=q’
q’
q(R,S)
т.е.
q’ есть
надмножество q
Если q’=q, то это разложение без потерь.
Пример:
R(X,Y,Z)
r1(X,Y) r2(X,Z) r1 r2 =
(X,Y,Z)
123 12 13 123
323 32 33 127
117 11 17 122
132 13 12 323
417 41 47 113
117
112
133
137
132
417
то есть это разложение с потерями.
Рассмотрим другое измерение:
r3(X,Y)
r4(Y,Z) r3 r4 = (X,Y,Z)
12 23 123
32 17 323
11 32 117
13 132
417
это разложение без потерь.