Алгоритм экспертных процедур

При использовании экспертных методов всегда присутствуют три крупных этапа: подготовка, опрос экспертов, обработка результатов.

Подготовка предполагает формирование целей применения экспертной процедуры и определение состава информации предполагаемой к получению у экспертов. Она включает определение при­знаков, по которым эксперты будут оценивать альтернативы и вида допустимого множества оценок. Кроме этого, в этап подготовки включается формирование группы экспертов. Для получения удовлетворительных результатов желательно иметь относительно большую группу экспертов, численность которой составляет не менее деся­ти высококвалифицированных специалистов. Однако в ряде случаев приходится отступать от такого принципа, ограничиваясь группой в составе трех-четырех человек.

Опрос экспертов определяется в конечном итоге предложенным им видом множества допустимых оценок и сводится к выбору каждым экспертом "своей" оценки, определенной по соответствующей совокупности признаков.

Обработка результатов опроса может проводиться различными методами (статическими, алгебраическими). Конкретный метод обработки результатов в значительной степени определяется видом множества допустимых оценок. По информации, полученной в резу­льтате обработки данных опроса, исследователь выносят суждение об удовлетворительности процедуры. Кроме этого, он может полу­чить информацию о свойствах группы экспертов и каждого эксперта в отдельности. Последнее позволяет при повторении этапов опроса провести корректировку.

В общем случае алгоритм экспертной процедуры может быть представлен в следующем виде.

1. Анализ исходной информация и построение множества воз­можных альтернатив для реализации сформулированной системы целей.

2. Анализ признаков возможных альтернатив, выделение си­стемы определяющих признаков и формирование комплекса аспектов (и критериев) для оценки альтернатив.

3. Нормирование множества допустимых оценок, организация и проведение экспертного опроса с целью решения одной из следующих задач;

• упорядочение альтернатив по каждому из аспектов

• получение численных оценок альтернатив по отдельным кри­териям;

• определение системы замещений, отражающих информацию о взаимной ценности отдельных критериев и (или) аспектов;

• определение области предпочтительных альтернатив при их совокупной оценке по системе критериев и (или) аспектов;

• выявление множества предпочтительных альтернатив.

4. Обработка результатов опроса экспертов:

• построение системы данных для решения задачи опроса;

• определение индивидуальных особенностей членов эксперт­ной группы;

• корректировка состава группы экспертов;

• принятие решения о удовлетворительности результатов; если результаты удовлетворяют исследователя, то переход к п. 5; если результаты не удовлетворяют исследователя, то возврат к п. 3.

5. Оформление результатов экспертной процедуры.

Метод Дельфи и его модификации

Этот метод в основном используется для определения обобщенных мнений относительно будущих ситуаций. Такая направленность метода определила его название: метод Дельфи (от названия греческого города. Дельфы где по мифологии свои предсказания осу­ществлял оракул в Храме Аполлона).

Основные принципы метода Дельфи могут с успехом применяться не только для задач прогнозирования, но и решения других вопросов. Суть этого метода сводится к последовательной реализа­ции простой системы правил:

• многотуровый характер опроса экспертов;

• количественный характер оценок, представляемых группой экспертов;

• использование статических методов обработки результатов опроса экспертов;

• межтуровое доведение результатов обработки до сведения экспертов;

• возможность учета компетентности экспертов путем введения¹ весовых коэффициентов при учете та их мнений об обработке.

Принципиально важным является при этом независимость формирования экспертами своего мнения (оценки).

При использовании рассматриваемого метода информация полученная от экспертов, подвергается статистической обработке по следующей схеме:

определяется значение прогнозируемой величины как средняя величина оценок экспертов:

где z_i – оценки экспертов;

N – число экспертов;

рассчитывается дисперсия оценок, определяющая разброс мнений экспертов;

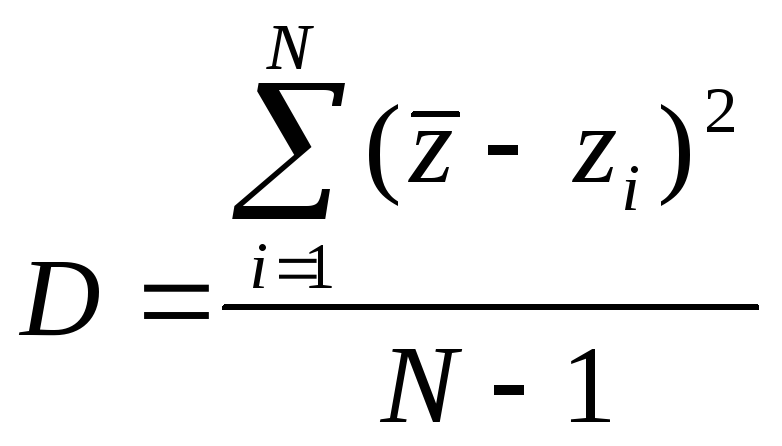
находится среднее квадратичное отклонение прогноза:

вычисляется так называемый коэффициент вариации, характеризующий единодушие экспертов:

определяется коэффициент компетентности экспертов с точки зрения всей группы экспертов как единого целого:

Полученные таким образом данные позволяют оценить диапа­зон прогнозируемой величины, в который она попадает с заданной вероятностью ρ. В предположении нормальности закона распределения мнений экспертов, что в большинстве случаев достаточно правдоподобно, диапазон определяется соотношением:

где τ - величина, зависящая от N и ρ, имеющая распределение Стьюдента с ( N - 1) степенями свободы и определяемая по таблицам в функции от (N-1) и (1- ρ) (например для N = 1 и ρ= 0,95 величина τ= 2,23).

Одной из модификаций метода Дельфи является использование мнений экспертов не в виде среднего значения оцениваемой величины z_i, а в виде диапазона, в который, по мнению эксперта. попадает эта величина (z_i^min, z_i^max).

В этом случае обработка результатов опроса имеет некото­рые особенности.

В предположении с равномерной плотности распределения в диапазоне (z_i^min, z_i^max) среднее значение оцениваемой величины для каждого i-го эксперта можно найти по соотношению

Полученные средние значения z_i, если их рассматривать как точечный прогноз, могут быть подвергнуты статистической обработке в соответствия с приведенными выше зависимостями

Однако наличие информации о диапазонах у каждого эксперта позволяет предложить и другой способ обработки информации:

для каждого эксперта определяется дисперсия значений оцениваемой величины:

коэффициент вариации для группы экспертов определяется по соотношению:

по величине дисперсии оценки эксперта может быть опреде­лен коэффициент η_i, характеризующий надежность данных, пред­ставленных экспертом, т.е. степень доверия к его информации:

с учетом доверия к эксперту оценка прогнозируемой величины группой экспертов рассчитывается по соотношению:

дисперсия прогнозируемой величины определяется в виде:

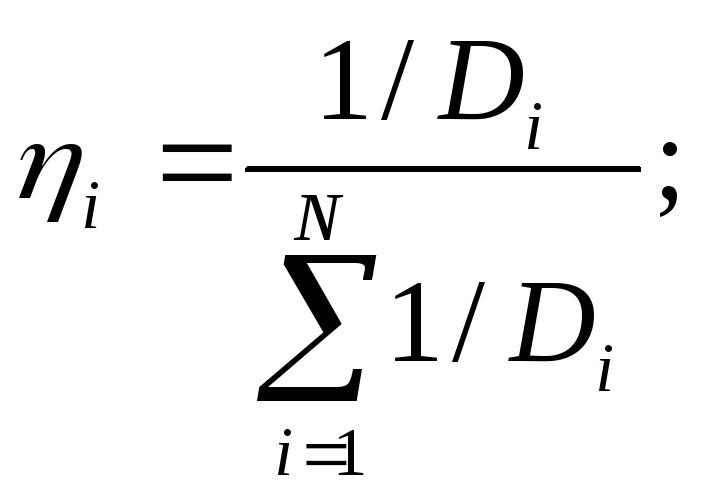
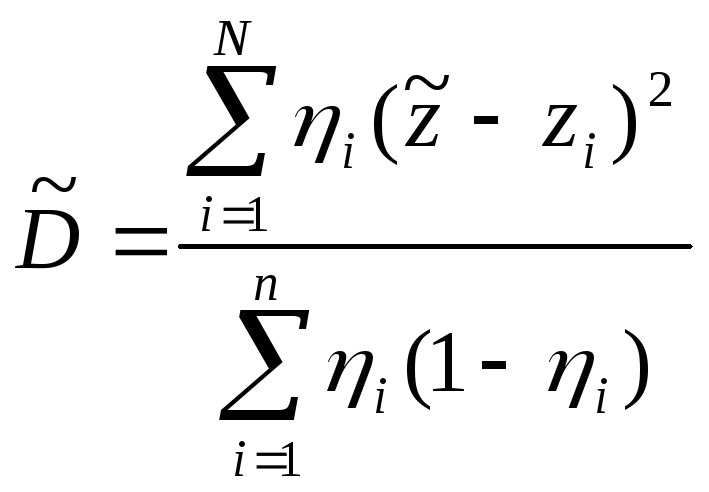
Как уже отмечалось выше, методы прогнозирования могут с успехом применяться для числовых оценок, определяющих некоторые альтернативы. При этом каждой альтернативе ставится в соответствие одна оценка. В ряде случаев для решения этой задачи яв­ляется удобной еще одна модификация метода Дельфи.

При организации опроса весь интервал, в котором может находиться оценка альтернативы, разбивается на т интервалов e₁,…,e_m:

Каждый из экспертов сообщает вероятность ρ_ij попадания оцениваемой величины в каждый из интервалов (где i - номер эксперта, j - номер интервала).

Суммарное мнение экспертов о попадании оцениваемой величины в каждый из интервалов определяется с учетом коэффициента доверия к эксперту величиной:

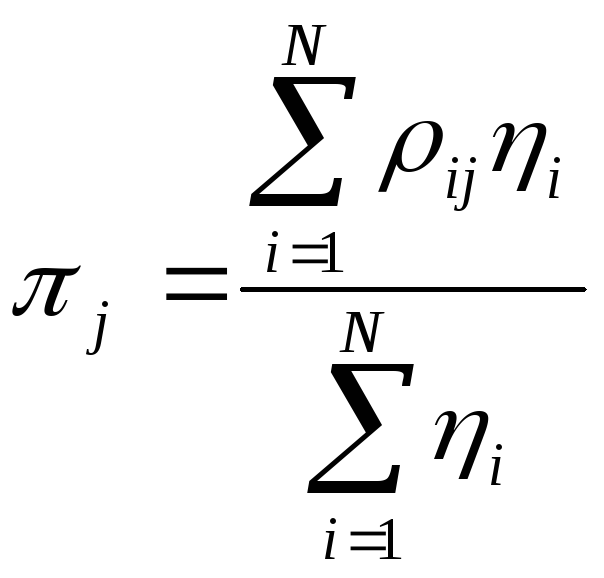
которая после нормирования

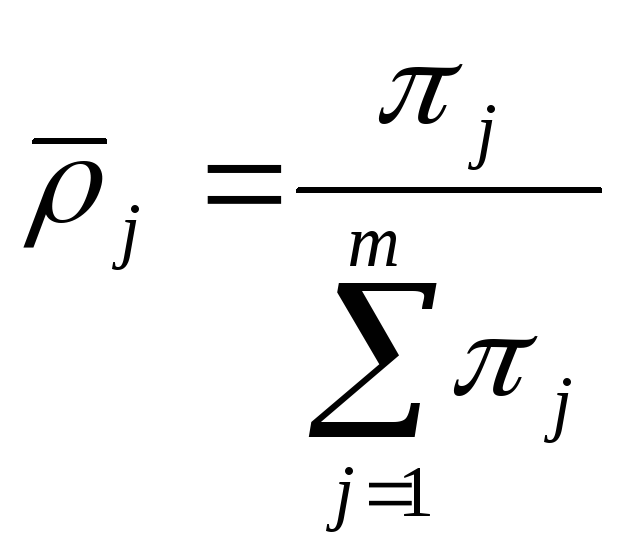
позволяет построить закон распределения вероятности попадания оцениваемой величины в интервалы оценки.

В качестве результирующей оценки рассматривается медиана построенного распределения, определяемая как величина оценки которая делит распределение на две равные части

Помимо медианы E₂ вычисляется диапазон квантилей

По опыту использования этой процедуры рекомендуется прекращать повторные опросы при уменьшении диапазона квантилей в 1,6 раза по сравнений со значением, полученным после первого тура опроса.