Министерство образования и науки рф

Московский государственный институт электроники и математики

(Технический университет)

Кафедра «Вычислительные системы и сети»

«МЕТОДЫ ЭКСПЕРТНЫХ ПРОЦЕДУР»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу

«СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ»

Москва 2005

ЦЕЛЬ РАБОТЫ

Цель работы – создание программы на основе методов принятия решений, использующих экспертные процедуры.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Экспертные процедуры

Альтернативы могут иметь различную форму представления. Они являются просто элементами множества Ω исходных альтернатив или представлены точками критериального пространства. Кроме этого, альтернативы можно упорядочить по некоторым аспектам.

Для возможности оптимизации и принятия проектных решений исключительно важным яв­ляется получение оценок рассматриваемых альтернатив. Такая задача получила название задачи оценивания (шкалирования). Ее суть сводится к тому, что каждому объекту ставится в соответствие число или совокупность чисел (вектор). В качестве объекта при этом могут выступать сами альтернативы, признаки альтернатив критерии или аспекты.

Задачи оценивания чаше всего решаются экспертными методами, т.е. путем организации опросов квалифицированных специалис­тов – экспертов (проектировщиков) с последующей обработкой полученной информации. Данные, получаемые от экспертов (для удобства их дальнейшей обработки и возможности получения достоверных результатов) в ходе решения одной проектной задачи должны носить унифицированный характер. Такая унификация реализуется путем введения системы допустимых оценок. Экспертам наиболее часто предлагаются следующие виды одинаковых множеств допустимых оценок.

Для попарного сравнения альтернатив задача заключается выявлении лучшего объекта, т.е. множество допустимых оценок Ω_g={0,1}, что позволяет при предъявлении альтернатив с и d реализовать правило выдачи оценки

При попарном сравнении множество Ω_g может быть расширено до трех элементов {-1,0,1} , что позволяет экспертам реали­зовать при сравнении альтернатив с и d правило

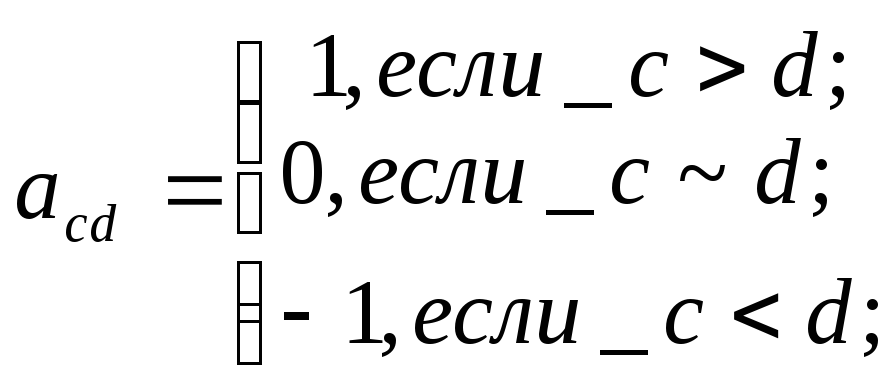
При одновременной оценке всех альтернатив экспертам пред­лагается установить ранг каждой альтернативы, т.е. расположить их в порядке возрастания (убывания) некоторого принципа, при этом допустимое множество оценок представляет собой совокупность перестановок порядковых номеров альтернатив

Ω_g={<1, 2,.., n, <1,3,...,n, 2>,…,<n,n-1,…, 2, 1>},

а результирующая оценка определяется как вектор номеров элемен­тов в данном упорядочении (задача ранжирования):

где К_j - номер j -й альтернативы при данном ранжировании.

Одновременную оценку всех альтернатив можно построить и на принципах задачи классификации, допустимое множество оценок при этом представляется как совокупность номеров классов, имеющих определенную признаки Ω_g = {1,…K}. Оценка в этой ситуа­ции определяется тем номером класса, к которому по мнению экс­перта принадлежит данная альтернатива (a =l , если альтернати­ва принадлежит классу с номером l).

При указании численных значений оце­нок каждой альтернативы эксперт называет одно (точка на оси кри­терия) или несколько (точка в критериальном пространстве) чисел оценка и этом определяется в масштабах соответствующих крите­риев: