4.2. Простейшие приближенные формулы для оценки низшей собственной частоты

Формула Релея. Пусть упругая система совершает собственные колебания с частотой p, причем смещение x_i массы m_i от равновесного положения изменяется по закону

(28)

Кинетическая энергия системы

. (29)

Потенциальная энергия системы изменяется пропорционально квадратам перемещений и может быть записана в форме

, (30)

где U₀ – энергия системы при амплитудных перемещениях x_i = u_i .

Из закона сохранения энергии следует

T+U= const,

поэтому должно быть

.

Таким образом, частота колебаний может быть определена по формуле Релея

, (31)

где - обобщенная масса системы при данной форме колебаний.

Если при вычислении формулы (31) задаваться формой к-того собственного колебания системы, то будет рассчитана к-тая собственная частота. Если задать форму колебаний, не слишком сильно отличающуюся от первой собственной формы, то формула Релея (31) позволяет определить приближенное значение первой частоты собственных колебаний системы. Причем принимая форму колебаний подобной статическим прогибам системы от некоторой подходящей нагрузки, можно существенно увеличить точность расчета за счет исключения операции дифференцирования.

Метод Граммеля. Позволяет повысить точность расчета путем замены дифференцирования интегрированием. Последовательность операций здесь такова.

• Задают форму колебаний и подсчитывают максимальную кинетическую энергию движения

. (32)

• Определяют максимальные силы инерции масс .

• Определяют внутренние силы в элементах системы, вызываемые нагрузками F_i.

• По внутренним силам вычисляют максимальную потенциальную энергию деформации U₀.

• Из равенства T_max = U₀ определяют частоту колебаний.

Формула Донкерлея. Так как метод Релея приводит к завышенному значению частоты колебаний, полезным является применение формулы, дающей заниженную частоту. Простейшей из такого рода формул является формула Донкерлея.

Точное значение собственной частоты многомассовой системы выразится формулой

. (33)

Частота колебаний той же системы, но с одной массой m_i, ,будет определяться по формуле

,

где δ_ii – податливость балки при приложении силы в точке закрепления массы m_i.

Приближенное значение частоты колебаний такой же системы можно определить по формуле Релея

. (34)

Сравнивая формулы (33) и (34) и учитывая, что формула Релея определяет завышенные значения частоты колебаний системы, получаем неравенство

.

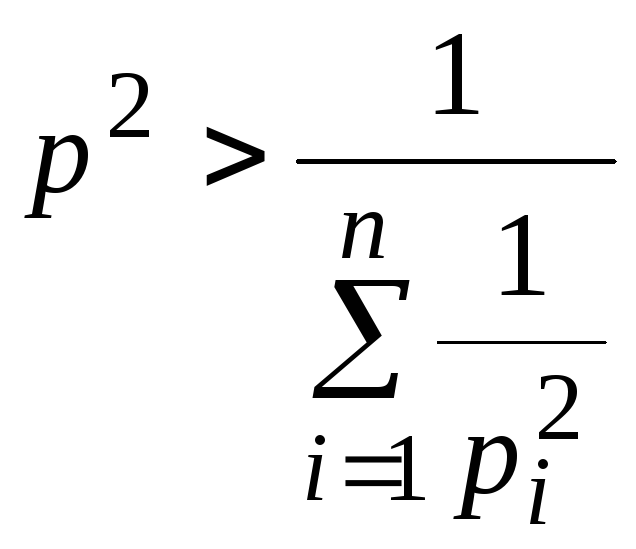Таким образом, приближенная формула Донкерлея

(35)

всегда дает преуменьшенное значение частоты.

Рассчитав частоту одной и той же системы по методу Релея и по формуле Донкерлея, мы получим интервал значений, содержащий истинную частоту колебаний.

4.3. Метод Релея – Ритца.

Метод Релея – Ритца основан на вариационном принципе Гамильтона, согласно которому для консервативной системы «действие», т. е. ,

имеет стационарное значение, здесь T – кинетическая, U – потенциальная энергия системы. Следовательно, вариация

. (36)

При этом на границах интервала интегрирования координаты не варьируются.

Записывая движение при собственных колебаниях в форме (28), подставляя соотношения (29) и (30), для интервала интегрирования (t₁=0, t₂=2π/p) приходим к уравнению

. (37)

В этом выражении частота p рассматривается как константа.

Зададим форму колебаний в виде ряда

, (38)

где a_r – неопределенные параметры; u^(r) – известные линейно независимые функции координат, удовлетворяющие условиям закрепления системы.

Количество слагаемых в выражении (38) определяется необходимой точностью расчета. С учетом (38), можно подсчитать значения иU₀, которые будут однородными квадратичными формами относительно параметров a_r. Тогда условия стационарности (37) приводит к системе уравнений

(39)

Уравнения (39) являются линейными и однородными относительно параметров a_r. Условие равенства нулю определителя системы (39) представляет собой уравнение частот

Это уравнение k- той степени относительно p². Если в выражении (38) для формы колебаний сохранить только одно слагаемое, то единственное уравнение системы (39) будет тождественно с формулой Релея. Сопоставляя метод Релея и метод Релея-Ритца, отметим, что в первом из них реальная система сходится к системе с одной степенью свободы, а во втором – к системе с k степенями свободы, где k – количество координатных функций, учитываемых в выражении (38) для формы колебаний.