отчет по 2 лабе

Пермский Государственный Технический Университет

Электротехнический факультет

Кафедра автоматики и телемеханики

Вычислительные методы.

Отчет по лабораторной работе №2.

Интегрирование функций.

Вариант №3.

Выполнили: студент гр. АТ-01-2

Лузин М.М. Лыткин П

Проверил: Данилова С.А.

Пермь 2003 г.

Цель работы: научиться применять численные методы вычисления определенных интегралов различных функций.

Задание: разработать программу вычисления определенного интеграла от функции

методом Гаусса для N=3 (степень полинома) с заданной погрешностью

Результат вывести в виде двух таблиц: 1 таблица без банкирования (т.е. погрешность, вычисляемая на каждом отрезке интегрирования не суммируется с погрешностью на последующем участке)

┌──┬────┬──── ┬──────┐

│ N │ Hi │ Qi │ Ei │

├──┼──── ┼────┼──────┤

………………………………………

Суммарная погрешность интегрирования должна быть меньше заданной.

2 таблица с банкированием, т.е. погрешность на каждом i-ом участке должна прибавляться к погрешности на i+1-ом участке. В результате интеграл будет подсчитан за меньшее число шагов, но с большей погрешностью, которая, тем не менее, не должна превышать заданную (должна равняться ей) (таблица выглядит аналогично).

Краткая теория.

Определенный интеграл может быть вычислен аналитически для заданной функции, непрерывной на интегрируемом отрезке, если известна первообразная интегрируемой функции. В тех случаях, когда первообразная сложна и определение ее затруднительно или невозможно, или когда функция задана таблично, целесообразно вычислять определенный интеграл численными методами.

Для метода Гаусса интеграл заменяется суммой

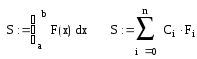
где Сi – коэффициенты

ti –

Можно построить поленом максимальной степени 2n-1 Простейший поленом t^k , где К=0, 1,…2n-1

K=0

K=1

K=2

K=2n-1

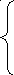
A₁+A₂+…A_n = 2

A₁t₁+A₂t₂+…A_nt_n = 0

A₁t²₁+A₂ t²₂+…A_nt²_n =

…………………………

A₁t^2n-1+A₂t^2n-1₂+…A_nt^2n-1_n = 0

Система нелинейная, порядок высокий, воспользуемся полиномом Лежандра для облегчения решения : k=0,1….n-1

по условию ортогональности k<n

L_n(t)=0 t=t_i - корни полинома Лежандра

В систему вместо t_i ставят корни полинома Лежандра

Переход к другим пределам:

- формула Гаусса

{Программа вычисляет интеграл методом Гаусса в адаптивном алгоритме}

Uses Crt;

Const b=5;a=0.6;e=0.001;

Function f(x:extended):extended;

Begin

f:=x*x*x*cos(3*ln(x))

End;

Function Gauss(a,b:extended):extended;

{Ф-ция вычисляет интеграл методом Гаусса по 4-м точкам}

var h,x4,x5:real;

Begin

h:=(b-a);

x4:=(b+a)/2+((b-a)*0.5773)/2;

x5:=(b+a)/2-((b-a)*0.5773)/2;

Gauss:=(h*(f(x4)+f(x5)))/2

End;

Function Gauss1(a,b:extended):extended;

{Ф-ция вычисляет интеграл методом Гаусса по 4-м точкам}

var h,x4,x5,x6:real;

Begin

h:=(b-a);

x4:=(b+a)/2+((b-a)*0.7746)/2;

x5:=(b+a)/2-((b-a)*0.7746)/2;

x6:=(b+a)/2;

Gauss1:=h*((5/9)*f(x4)+(5/9)*f(x5)+(8/9)*f(x6))/2

End;

{Основная программа}

Var

xl,xm,xr,x :extended;{Значение x на краях отрезка и посередине}

S,P,Q,h,ee:extended;{Значение интеграла}

ei,hi,Qi:array[1..1000]of extended;

xl1,xm1,xr1,x1 :extended;{Значение x на краях отрезка и посередине}

S1,P1,Q1,h1,ee1:extended;{Значение интеграла}

ei1,hi1,Qi1:array[1..1000]of extended;

i,j:byte;

BEGIN

ClrScr;

Writeln('Вычисление интеграла без банкирования');

WriteLn('j':5, '|', 'h(i)':17,'Q(i)':21,'e(i)':17);

WriteLn('-------------------------------------------------------------');

xl:=a;xr:=b;i:=0;

repeat{Цикл поиска отрезка,удовлетворяющего неравенству}

repeat h:=xr-xl;{Размер отрезка}

P:=Gauss(xl, xr);

xm:=(xl+xr)/2;

Q:=Gauss(xl, xm)+Gauss(xm, xr);

x:=xr;

xr:=xm;

ee:=Abs(P-Q)/31

until ee<=h*e/(b-a);

i:=i+1;

Qi[i]:=Q;

hi[i]:=h;

ei[i]:=ee;

xl:=x;

xr:=b

until x=b;

h:=0;S:=0;ee:=0;

for j:=1to i do begin WriteLn(j:5, '|', hi[j], '|', Qi[j], '|', ei[j]);

S:=S+Qi[j];

h:=h+hi[j];

ee:=ee+ei[j]

end;

WriteLn('---------------------------------------------------------------');

WriteLn(' ':5, ' ', h:5:5, ' | ', S:7:7, ' | ' , ee:5:5);

WriteLn;

WriteLn('Задана погрешность : ',e:5:5);

WriteLn('Значение интеграла : ',S:7:7);readln;

xl1:=a;xr1:=b;i:=0;

repeat{Цикл поиска отрезка,удовлетворяющего неравенству}

repeat h1:=xr1-xl1;{Размер отрезка}

P1:=Gauss1(xl1, xr1);

xm1:=(xl1+xr1)/2;

Q1:=Gauss1(xl1, xm1)+Gauss1(xm1, xr1);

x1:=xr1;

xr1:=xm1;

ee1:=Abs(P1-Q1)/31

until ee1<=h1*e/(b-a);

i:=i+1;

Qi1[i]:=Q1;

hi1[i]:=h1;

ei1[i]:=ee1;

xl1:=x1;

xr1:=b

until x1=b;

h1:=0;S1:=0;ee1:=0;

Writeln('Вычисление интеграла c банкированием');

WriteLn('j':5, '|', 'h(i)':17,'Q(i)':21,'e(i)':17);

WriteLn('-------------------------------------------------------------');

for j:=1to i do begin

S1:=S1+Qi1[j];

h1:=h1+hi1[j];

ei1[j+1]:=ei1[j+1]+ei1[j];

ee1:=ee1+ei1[j];

WriteLn(j:5, '|', hi1[j], '|', Qi1[j], '|', ei1[j]*10);

end;

WriteLn('---------------------------------------------------------------');

WriteLn(' ':5, ' ', h1:5:5, ' | ', S1:5:5, ' | ' , ee1*10:5:5);

WriteLn('Задана погрешность : ',e:5:5);

WriteLn('Значение интеграла : ',S1:5:5);readln

END.