кинематика / Glava_6

Глава 6. Общий случай движения НМС

6.1. Уравнения движения НМС

В общем случае движения НМС, когда она является свободной, НМС движется как угодно по отношению к неподвижной системе отсчета О₁х₁у₁z₁ (рис. 62). Выбрав в качестве полюса произвольную точку О НМС, свяжем с ней оси декартовой системы координат О, которые при движении НМС будут перемещаться вместе с полюсом поступательно.

Кроме того, построим неизменно связанную с НМС декартову систему координат Охуz с началом также в полюсе О.

Положение НМС в системе отсчета О₁х₁у₁z₁ будет известно, если известно положение полюса О, т.е. его координаты х_1О, y_1О, z_1О и положение НМС по отношению к осям О, определяемое, как и в случае сферического движения НМС (глава 5), углами Эйлера , ,  (рис. 62).

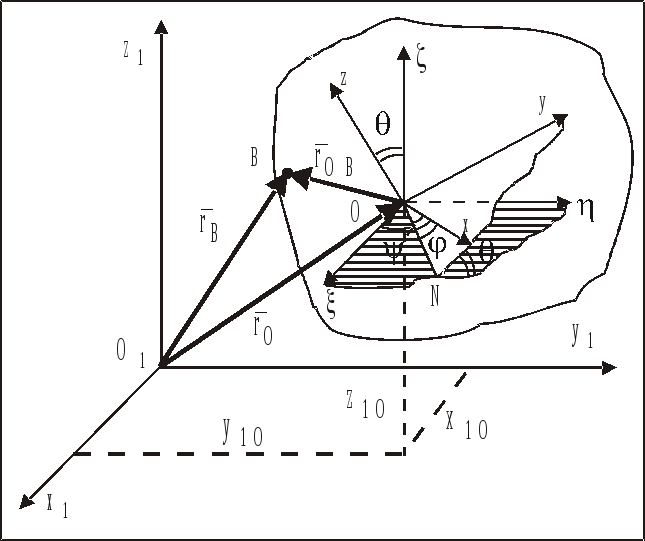
Рис. 62

Следовательно, уравнения движения свободного НМС, позволяющие найти ее положение по отношению к системе отсчета О₁х₁у₁z₁ в любой момент времени, имеют вид:

(6.1)

Эти функции должны быть однозначными, непрерывными и дважды дифференцируемыми. Уравнений движений свободной НМС шесть, столько же, сколько обобщенных координат у НМС.

Движение НМС относительно точки О, как следует из главы 5, представляет собой последовательность мгновенных вращательных движений относительно мгновенных осей вращения, проходящих через точку О, с угловой скоростью и угловым ускорением .

6.2. Скорость точки НМС

Радиус-вектор , определяющий положение точки, принадлежащей НМС, по отношению к неподвижной системе координат О₁х₁у₁z₁, можно представить в виде:

, (6.2)

где определяет положение полюса О по отношению к неподвижной системе координат О₁х₁у₁z₁, а определяет положение точки по отношению к подвижной системе координат Охуz ( меняется только по направлению и не меняется по модулю).

Взяв производную по времени от соотношения (6.2), получаем:

.

Так как здесь а, на основании формулы (5.7) , то в результате получим формулу:

(6.3)

где .

Теорема: Скорость точки свободной НМС в общем случае движения равна векторной сумме скорости точки НМС, выбранной в качестве полюса, и скорости этой точки от мгновенного вращательного движения НМС вокруг мгновенной оси вращения, проходящей через этот полюс.

6.3. Независимость угловой скорости и углового

ускорения НМС от выбора полюса

Используя формулу (6.3), докажем, что угловая скорость движения НМС относительно мгновенной оси вращения, проходящей через полюс, не зависит от выбора полюса.

Выберем два полюса О и О₂, а соответствующие им угловые скорости обозначим через и соответственно (рис. 63).

Рис. 63

На основании формулы (6.3) можно записать:

Подставив третье равенство в первое и сравнивая первые два, получим:

или

Так как , то

, следовательно, .

Взяв производную по времени от равенства , получим , т. е. .

Угловые скорость и ускорение свободного НМС в общем случае движения не зависят от выбора полюса.

6.4. Ускорение точки НМС

Для определения ускорений точек НМС в общем случае его движения возьмем производную по времени от выражения (6.3):

.

Так как здесь

,

то в результате получим формулу:

. (6.4)

Сравнивая полученное выражение с равенством (5.13), можно сделать вывод, что

,

где – ускорение от движения точки В относительно полюса О. Тогда соотношение (6.4) примет вид:

. (6.5)

Теорема: Ускорение точки свободной НМС в общем случае движения равно векторной сумме ускорения точки, выбранной в качестве полюса, и ускорения этой точки от мгновенного вращательного движения НМС вокруг мгновенной оси вращения, проходящей через этот полюс.

122