
- •Лекция 2. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ2.1
- •1.3. Электростатическое поле. Напряженность электростатического поля
- ••Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что
- ••ЭМП – есть не абстракция, а объективная реальность – форма существования материи, обладающая
- ••Силовой характеристикой поля, создаваемого зарядом q, является отношение силы действующей на заряд к
- •• Или в векторной форме
- ••Вектор напряженности электростатического поля равен силе, действующей в данной точке на помещенный в
- •1.4. Сложение электростатических полей.
- ••Результирующая сила определится выражением:
- ••Напряженность результирующего поля системы точечных зарядов равна векторной сумме напряженностей полей, созданных в
- •Пример 1
- ••В данном случае:
- ••Рассмотрим другой пример. Найдем
- ••Если поле создается не точечными зарядами, то используют обычный в таких случаях прием.
- ••Для решения подобных задач пользуются соответствующими значениями плотности заряда:
- ••Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного,
- ••Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy,
- •• Вектор dE имеет проекции dEx и dEy причем
- •тогда
- ••Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до
- ••Задание: по тонкому кольцу радиуса R равномерно распределен заряд q. Определить Е в
- •1.5. Электростатическое поле
- ••Пример 1. Найдем Е в точке А на прямой, проходящей через центр диполя
- ••Из подобия заштрихованных треугольников можно записать:
- ••Обозначим вектор: Р ql–
- •• Пример 2. На оси диполя, в точке В
- •• Пример 3. В произвольной точке С
- •• Электрическое поле диполя.
- ••Из приведенных примеров видно, что напряженность электрического поля системы зарядов равна геометрической сумме

тогда |
E Ex dEcosθ |
λ |
|
|
cosθdy |
||||||||
4πε0 |
|
|
x2 y2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y xtgθ, |
||||||
Теперь выразим y через θ. Т.к. |
|
|
|
|
|
|
|||||||
тоdy xdθ / cos |
2 θ |
|
|
|
x2 y2 |
x2 / cos2 |
|||||||
|
|
|
|
и |
|
π |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
тогда |
|
|
λ |
1 |
2 |
|
λ |
|||
|
|
|
|
E |
|
|
|
πcosθdθ |
|
. |
|||
|
|
|
|
4πε0 |
x |
2πε0 x |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
•Таким образом, напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.

•Задание: по тонкому кольцу радиуса R равномерно распределен заряд q. Определить Е в точке А
1.5. Электростатическое поле
диполя
•Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов, расстояние между которыми значи – тельно меньше расстояния до тех точек, в которых определяется поле системы
•Плечо диполя – вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.

•Пример 1. Найдем Е в точке А на прямой, проходящей через центр диполя и перпендикулярной к оси.
E E |
1 |
|
|
|
q |
|
|
|
q |
|
4πε0 |
|
r |
2 |
l |
2 |
4πε0r2 |
т.к. l r |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|

•Из подобия заштрихованных треугольников можно записать:
E |
|
|
|
l |
|
|
|
|
l |
отсюда |
E |
|
|
|
|
2 |
1 |
r |
|||
|
|
2 |
|
l |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
r |
|
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
•Обозначим вектор: Р ql–
электрический момент диполя (или дипольный момент) – произведение положительного заряда диполя на плечо l.
•Направление P совпадает с направлением l , т.е. от отрицательного заряда к положительному.
• Тогда, учитывая что |
|
получим: |
|||||
|
P |
ql P |
|||||
E |
|
|
P |
||||
|
или |
E |
|
|
|||
4πε0r3 |
|||||||
4 0r3 |
|||||||
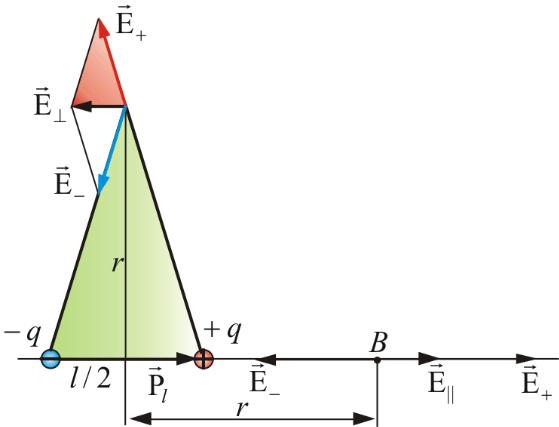
• Пример 2. На оси диполя, в точке В
|
2ql |
|
|
|
2P |
|
|
|
E|| |
|
|
или |
E|| |
|
. |
||
|
4πε0r |
3 |
4πε0r |
3 |
||||
|
|
|
|
|
|
|
||
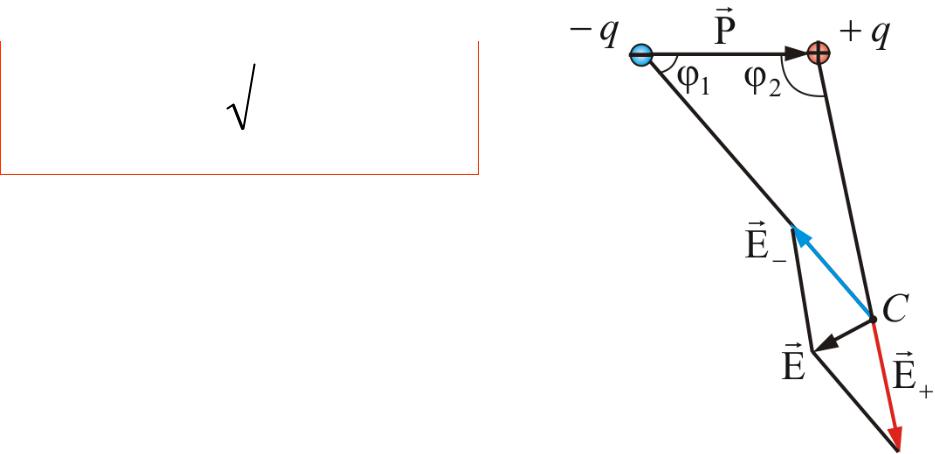
• Пример 3. В произвольной точке С
|
P |
|
|
|
|
E |
|
3cos2 |
φ 1, |
||
4πε0r3 |
|
||||
|
|
|
|
|
|
где φ φ1 φ2 При :
φ φ |
2 |
π |
, |
E |
P |
; |
|
||||||
1 |
2 |
|
1 |
4πε0r3 |
|
|
|
|
|
|
|
φ φ |
2 |
0, |
Е |
2P |
|
||||
1 |
|
2 |
4πε0r3 |
|
|
|
|
|

