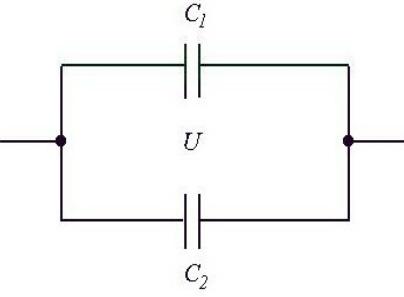
8.4.2. Соединение конденсаторов
Емкостные батареи – комбинации параллельных и последовательных соединений конденсаторов.
1) Параллельное соединение (рис. 5.6):
|
|
|
|
Общим является напряжение U |
||
|
|
|
|
|
q1 |
= C1U; |
|
|
|
|
|
q2 |
= C2U; |
|
|
|
|
Суммарный заряд: |
||
|
|
|
|
q = q1 + q2 = U(C1 + C2). (8.4.9) |
||
Результирующая емкость: |
|
|||||
|
C |
q |
C C |
|
|
(8.4.10) |
|
|
2 |
|
|
||
|
U |
1 |
|
|
||
|
|
|
|
|
||
Сравните с параллельным соединением сопротивлений R: |
||||||
1 |
1 |
1 |
(8.4.11) |
|||
|
|
|
|
|
|
|
|
R |
R |
R |
|
||
|
|
1 |
2 |
|
||
Таким образом, при параллельном соединении конденсаторов, их емкости складываются.
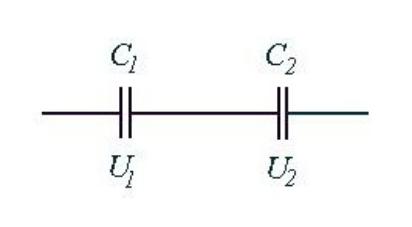
2) Последовательное соединение : |
|
|
|
|
|
|
|
q |
|
|||||||||||
Общим является заряд q |
U1 |
q |
|
; |
|
U2 |
|
|
; |
|||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
C1 |
|
|
1 |
|
|
C2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
U Ui q |
|
|
|
|
(8.4.12) |
||||||||||
|
|
|
|
|
Ci |
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
C1 |
C2 |
|
|
|
|
|
||||||
1 |
1 |
|
|
|
C |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
(8.4.14) |
R = R1 + R2 |
|
|
|
|
|
(8.4.13) |
|||||||||
|
C |
Ci |
|
|
|
|
|
|||||||||||||
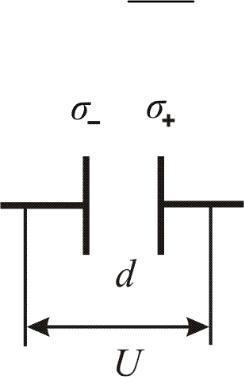
8.4.3. Расчет емкостей различных конденсаторов
1. Емкость плоского конденсатора.
E ;
0
|
|
|
|
|
|
x1 |
σ |
|
|
|
|
|
|
|
|
|
|
|
φ |
φ |
2 |
|
Edx |
|
d |
|
|
1 |
|
|
|
ε0 ε |
|||
где d = x |
– x |
|
|
|
x2 |
|||
|
– расстояние между |
|||||||
, |
2 |
1 |
|
|
|
|
|
|
пластинами. |
|
|
q σS |
|
|
|||
Так как заряд |
|
, то |
||||||
C |
q |
|
|
ε |
ε |
S |
|
|
φ |
φ |
|
d |
|
||||
|
2 |
0 |
|
(8.4.16) |
||||
|
1 |
|
|
|
|
|
||
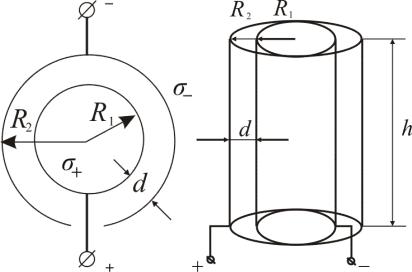
2. Емкость цилиндрического конденсатора.
Разность потенциалов между обкладками цилиндрического
конденсатораλ |
|
|
ln |
R2 |
(8.4.17) |
|
φ |
2πε |
0 |
ε |
R |
|
|
|
|
|
|
1 |
|
|
где λ – линейная плотность заряда, R1и R2 – радиусы цилиндрических обкладок.
q = λl, (l – длина конденсатора) |
lλ ln |
R2 |
|
|
q |
|
|||
R |
|
|
|
||||||
|
|
|
φ |
|
|
|
|
||
|
|
|
|
1 |
|
|
|
(8.4.18) |
|
|
2πε0εl |
|
C |
||||||
Cцил. |
2πε0εl |
|
|
||||||
|
|
|
|||||||
ln R |
|
|
|
|
|
|
|||
|
|
R2 |
|
|
|
|
|
|
(8.4.19) |
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
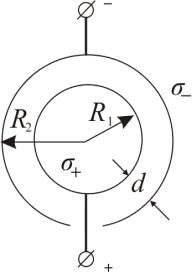
Понятно, что зазор между обкладками мал: d = R2 d << R1, тогда
ln |
R2 |
|
R2 R1 |
|
R |
R |
|||
|
|
|||
|
1 |
1 |
||
C |
цил. |
|
2πε0εlR1 |
ε |
ε |
S |
||
d |
||||||||
|
|
R R |
0 |
|
||||
|
|
|
2 |
1 |
|
|
|
|
3. Емкость шарового конденсатора.
–R1, то есть
(8.4.20)
φ1 φ2 |
q |
|
|
1 |
|
1 |
|
(8.4.21) |
|
|
|
|
|||||
4πε |
|
R |
R |
|||||
ε |
|
|
||||||
|
0 |
|
|
1 |
|
2 |
|
|
Это разность потенциалов между обкладками
шарового конденсатора, где R1 и R2 – радиусы шаров.
|
|
q |
, |
C |
4πε0εR1R2 |
(8.4.22) |
Рис. 8.10 |
C |
R2 R1 |
|
В шаровом конденсаторе R1 ≈ R2; S = 4πR2; R2 – R1 = d – расстояние между обкладками. Тогда
Cшар. |
4πε0εR2 |
ε0 |
ε |
S |
. |
(5.4.23) |
d |
d |
|
||||
|
|
|
|
|
Таким образом, емкость шарового конденсатора,
Сшар. ε0ε dS ,
что совпадает с емкостями плоского и цилиндрического конденсатора.
8.4.4. Энергия заряженного конденсатора
Если замкнуть обкладки конденсатора, то по проволоке потечет ток, который может даже расплавить ее. Значит, конденсатор запасает энергию. Вычислим ее.
Конденсатор разряжается U' – мгновенное значение напряжения на обкладках. Если при этом значении напряжения между обкладками проходит заряд dq, то работа
dA = U'dq. |
(8.4.24) |
Работа равна убыли потенциальной энергии конденсатора:
dA = – dWc. |
(8.4.25) |
Так как q = CU, то dA = CU'dU', а полная работа
A dA.
|
0 |
|
|
|
1 CU 2 |
(8.4.26) |
A W C U dU |
||||||
c |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
U |
|
|
|
||
|
Wc |
|
CU 2 |
|
(8.4.27) |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Энергию конденсатора можно посчитать и по другим формулам:
W |
|
q2 |
|
1 |
qU |
|
|
|
(8.4.28) |
||||
|
|
|||||
c |
|
2C |
|
2 |
|
|
|
|
|
|
|
8.5. Энергия электростатического поля
Где же сосредоточена энергия конденсатора? На обкладках? То есть на зарядах? А может, в пространстве между обкладками? Только опыт может дать ответ на этот вопрос.
В пределах электростатики дать ответ на этот вопрос |
||||||||||
невозможно. Поля и заряды, их образовавшие не могут |
||||||||||
существовать обособленно. Их не разделить. Однако |
||||||||||
переменные поля могут существовать независимо от |
||||||||||
возбуждавших их зарядов (излучение солнца, радиоволны, …) |
||||||||||
и они переносят энергию. Эти факты заставляют признать, что |
||||||||||
носителем энергии является электростатическое поле. |
||||||||||
Носителем энергии в конденсаторе, Wc является |
||||||||||
электростатическое поле. |
|
|
|
Найдем Wc: |
||||||
|
CU 2 |
|
ε0εSU 2 |
d |
|
ε0ε U |
2 |
|||
Wc |
|
|
|
|
|
|
|
|
Sd |
|
2 |
2d |
d |
2 |
|||||||
|
|
|
d |
|
|
|||||
U |
|
|
|
|
Sd = V – объем. Отсюда: |
|
|
|
|
d E; |
|
|
|
|
W |
ε0εE2 |
V |
|
|
2 |
|
|||
(8.5.1) |
c |
|
|
|
|
|
|
|
|
|
|
|
||
Если поле однородно, заключенная в нем энергия |
||||
распределяется в пространстве с постоянной плотностью. Тогда можно посчитать удельную энергию ωуд:
(8.5.2) |
уд W |
; |
ωуд |
ε0εE2 |
|
|
|||||
|
V |
|
2 |
|
|
ED
Или, так как D = ε0εE, то (8.5.3)ωуд 2
Эти формулы справедливы для однородного поля.
Если поле создано двумя точечными зарядами q1 и q2, то для
каждого из них |
|
|
|
|
|||
W |
q φ |
Здесь φ |
– потенциал поля, создаваемого зарядом q |
|
|||
1 |
; |
|
2 |
||||
|
1 12 |
W2 |
12 q2φ21 |
|
|||
в точке, где расположен заряд q1, φ21 |
– потенциал поля от заряда q1 |
||||||
в точке с зарядом q2.