
- •Лекция 6. Расчет потенциалов простейших электростатических полей
- •6.1. Уравнения Лапласа и
- •Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами
- •6.2. Силовые линии и
- •Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется
- •Линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны
- •Формула E grad φ выражает связь потенциала с напряженностью и позволяет по
- ••Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут
- •6.3. Расчет потенциалов простейших электростатических полей
- •Мы показали, что напряженность связана с
- •Чтобы получить выражение для потенциала
- •На рисунке 6.1,б изображена зависимость напряженности E и потенциала φ от расстояния между
- •6. 3.2. Разность потенциалов между точками поля, образованного бесконечно
- •Тогда, т.к.
- •6.3.3. Разность потенциалов между обкладками цилиндрического конденсатора
- •6. 3.4. Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
- ••Из полученных соотношений можно сделать следующие выводы:
- •Сегодня: пятница 5 Июль, 2019
- •До сих пор мы рассматривали электростатические поля и взаимодействие зарядов в вакууме. Как
- •Электрический диполь.
- •Диполь во внешнем поле
- •4.1.Поляризация диэлектриков
- ••В идеальном диэлектрике свободных зарядов, то есть способных перемещаться на значительные расстояния
- ••Смещение электрических зарядов вещества под действием электрического поля называется поляризацией.
- •Поляризуемость диэлектрика включает составляющие – электронную, ионную и ориентационную (дипольную).
- •• Главное в поляризации – смещение зарядов в электростатическом поле. В результате, каждая
- ••Внутри диэлектрика электрические заряды
- ••Обозначим E'– электростатическое поле связанных зарядов. Оно направлено
- •• Поместим диэлектрик в виде параллелепипеда в
- ••Введем новое понятие – вектор
- •• С учетом этого обстоятельства,
- ••Вектор поляризации можно представить так:
- •Следовательно, и у результирующего поля E изменяется, по сравнению с E0 ,только нормальная
- •• Величина ε 1 χ характеризует электрические свойства диэлектрика.
- •• График зависимости напряженности электростатического поля шара от радиуса, с учетом диэлектрической проницаемости
- •4.2.Различные виды диэлектриков
- ••Рассмотрим основные свойства сегнетоэлектриков:
- ••Это свойство называется диэлектрическим гистерезисом
- ••4. Наличие точки Кюри – температуры, при которой (и выше) сегнетоэлектрические свойства пропадают.
- ••Стремление к минимальной потенциальной энергии и наличие
- ••Среди диэлектриков есть
- •Пьезоэлектрики
- ••Сейчас известно более 1800 пьезокристаллов.
- •4.2.3. Пироэлектрики
- •Все пироэлектрики являются пьезоэлектриками, но не наоборот. Некоторые пироэлектрики обладают сегнетоэлектрическими свойствами.
- •В качестве примеров использования
- •4.3. Вектор электрического смещения D
- ••Главная задача электростатики – расчет электрических полей, то есть E
- ••Для упрощения расчетов была введена новая векторная величина – вектор
- •Зная D и ε, легко рассчитывать
- •• Для точечного заряда в вакууме
- •4.4. Поток вектора электрического смещения.
- •В однородном электростатическом поле
- •Теорему Остроградского-Гаусса для вектора D получим из теоремы Остроградского-Гаусса для вектора E :
- •• Теорема Остроградского-Гаусса для D
- •4.5. Изменение E и D на границе
- •• Пусть ε2 ε1.
- ••Образовавшиеся поверхностные заряды изменяют только нормальную составляющую E
- •• То есть направление вектора E
- ••Рассмотрим изменение вектора D и его проекций Dn и Dτ
- ••Объединим рисунки 4.12 и 4.13 и проиллюстрируем закон преломления для
- ••Как видно из рисунка, при переходе из одной диэлектрической среды в другую вектор
- •Сегодня: пятница 5 Июль, 2019
- •Сегодня: пятница 5 Июль, 2019

Лекция 6. Расчет потенциалов простейших электростатических полей
6.1.Уравнения Лапласа и Пуассона
6.2.Силовые линии и эквипотенциальные поверхности
6.3.Расчет потенциалов простейших электростатических полей

6.1. Уравнения Лапласа и
Пуассона
Часто предпочтительным методом нахождения Е является сведение задачи к решению дифференциального уравнения для потенциала.
Теорема Гаусса: E ρ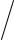 ε0 и E - следовательно
ε0 и E - следовательно
2 - ρ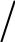 ε0 2 - оператор Лапласа (лапласиан)
ε0 2 - оператор Лапласа (лапласиан)
div grad 2
2x 2y 2z |
2 |
|
2 |
|
2 |
|||
x |
2 |
y |
2 |
z |
2 |
|||
|
|
|
|
|
|
|||
2 ρ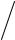 ε0 - уравнение Пуассона
ε0 - уравнение Пуассона
В области пространства, где заряды отсутствуют =02 0 - уравнение Лапласа

Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами

6.2. Силовые линии и
эквипотенциальные поверхности
Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением . E
Отсюда следует, что напряженность равна разности потенциалов U на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить
φ между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки.
В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить E наиболее просто:
U |
(5.6.1) |
E l |
|
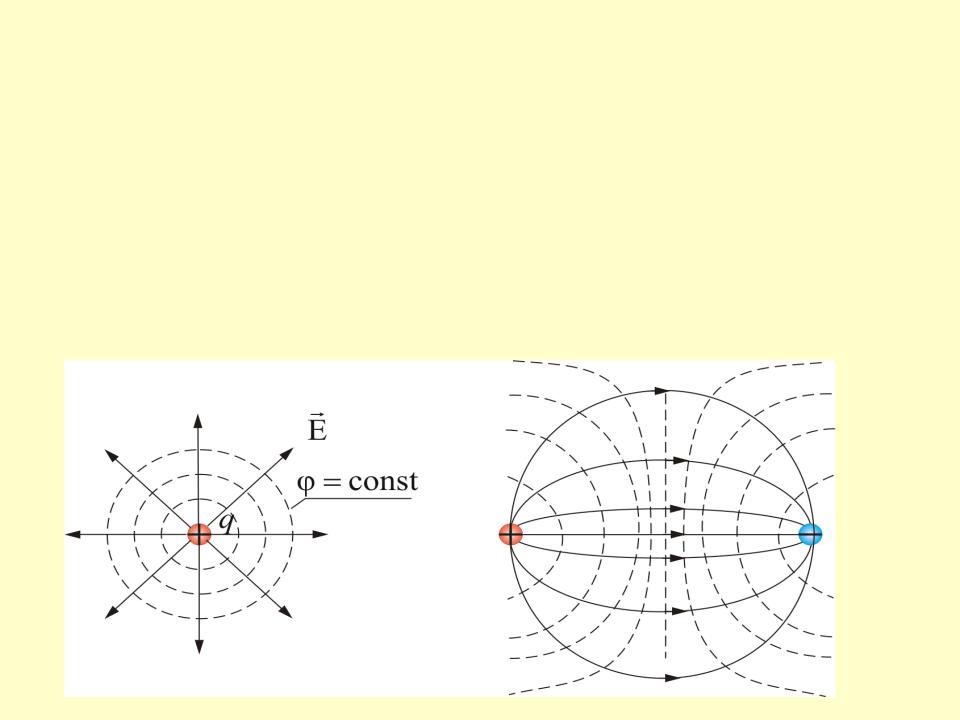
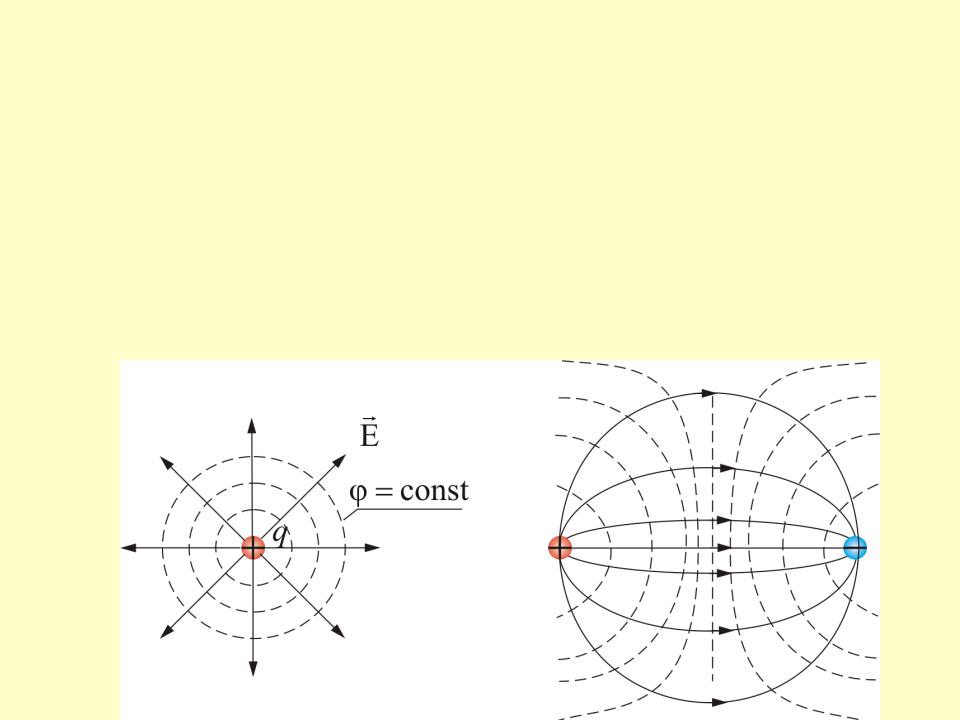
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется
эквипотенциальной поверхностью.
Уравнение этой поверхности
(6.6.2)
φ φ(x, y, z) const.
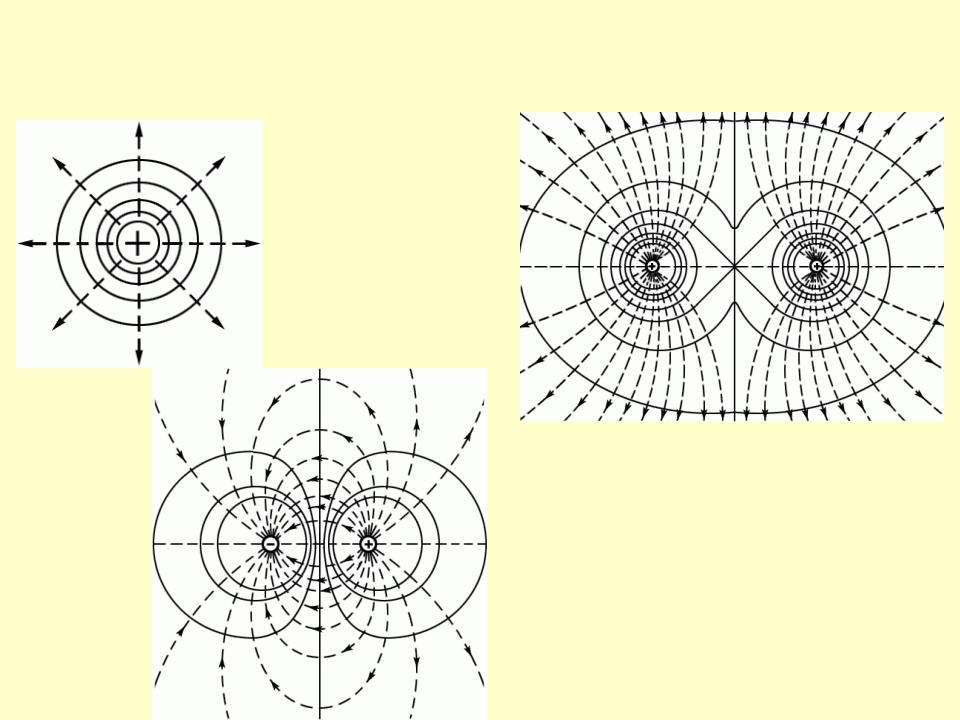
Линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны

Формула E grad φ выражает связь потенциала с напряженностью и позволяет по
известным значениям φ найти напряженность поля в каждой точке.
Можно решить и обратную задачу, т.е. по известным значениям E в каждой точке поля найти разность потенциалов между двумя
произвольными точками поля.
2
φ1 φ2 (E,dl).
1

2
φ1 φ2 (E,dl).
1
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути.
Для обхода по замкнутому контуру φ1 φ2получим:
т.е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля
вдоль любого замкнутого контура равна нулю.
(E,dl) 0,
Поле, обладающее этим свойством, называется потенциальным.
•Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность
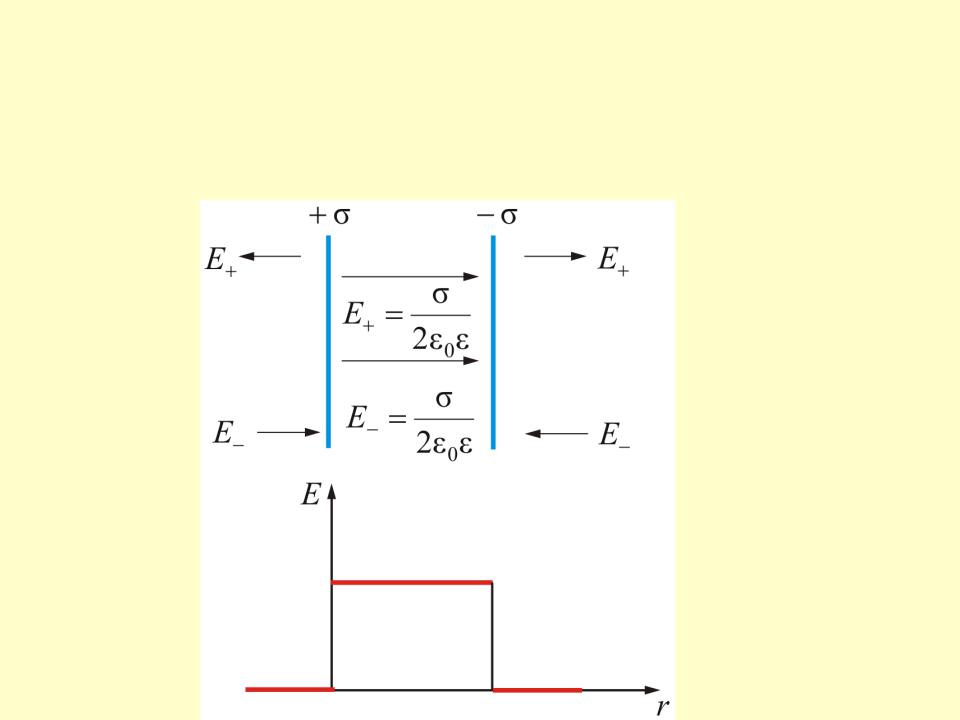
6.3. Расчет потенциалов простейших электростатических полей
6.3.1.Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
Рис. 6.1,а
