Такая форма более удобна, потому что проще измерить f, чем кривизну и показатель преломления линзы. Если нам не нужно самим конструировать линзу или изучать в подробностях весь процесс, а достаточно достать линзу с полки, то нас будет интересовать только величина f, а не n или R!
Пусть s становится меньше f. При s < f обратная величина (1/s) больше (1/f) и поэтому s' отрицательна. Это означает, что исходящие из точки О лучи (рис. 3.2) преломляются на поверхности, но в фокус не собираются, так как точка О расположена слишком близко к поверхности, и лучи становятся расходящимися. Но они начинают расходиться так, как будто бы вышли из точки О' вне линзы. Эта точка есть кажущееся или
Рис. 3.3. Мнимое изображение точки О – точка О'
мнимое изображение (рис.3.3). Изображение О' на рис. 3.2 называется действительным изображением. Действительное изображение возникает, когда свет действительно проходит через точку. Но если кажется, что свет исходит из некоторой фиктивной точки, не совпадающей с действительным источником, то эта точка и есть мнимое изображение. Для отрицательных s' точка О' находится по другую сторону поверхности.
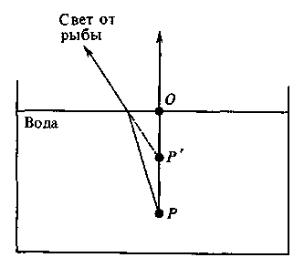
Рассмотрим случай R = ; при этих условиях (1/s) + (n/s') = 0, s = –ns. Это означает, что если из плотной среды смотреть на некую точку в разреженной среде, то она будет казаться дальше в n раз. Можно прочитать уравнение и наоборот: s = –s /n – при взгляде на объект, находящийся в плотной среде за плоской поверхностью раздела, будет казаться, что он расположен к нам ближе (рис. 3.4).
Когда мы смотрим сверху на дно плавательного бассейна, он кажется нам мельче в 3/4 раза, чем он есть на самом деле; эта цифра есть обратная величина показателя преломления воды n = 1,33.
3.2. Сферическое зеркало
Падающий на вогнутое зеркало пучок лучей, параллельных оптической оси зеркала, после отражения собирается в фокусе зеркала F. Фокус находится в середине отрезка, соединяющего центр кривизны сферической поверхности зеркала и вершину зеркала (полюс). Фокусное расстояние f = R/2, где R радиус
кривизны поверхности зеркала. Когда предмет находится на расстояниях от вогнутого зеркала, превышающих фокусное расстояние, изображение предмета действительное, перевернутое (рис. 3.5).
Рис. 3.5. Предмет S находится за фокусом изображение
перевернутое, увеличенное, исключая положение в точке р
Рис. 3.6. Предмет S находится перед фокусом изображение мнимое, прямое,
увеличенное
Изображение предмета, расположенного ближе фокуса, мнимое, прямое, увеличенное (рис. 3.6). Оно находится за зеркалом.
Падающий на выпуклое зеркало параллельный пучок лучей отражается так, будто все лучи выходят из фокуса F, находящегося за зеркалом на расстоянии R/2. Чтобы вывести формулы для сферического зеркала, полезно принять следующие условия:
1)расстояние до объекта s положительно, если точка О расположена перед зеркалом;
2)расстояние до изображения s' положительно, если точка О' расположена за зеркалом;
3)радиус кривизны поверхности положителен, если центр находится за зеркалом.
Например, на рис. 3.5 s, s' положительны, а R отрицательно; на рис. 3.6 s положительна, a s' и R отрицательны.
Рис. 3.7. Изображения в выпуклом зеркале независимо от положения предмета является мнимым, уменьшенным, прямым