начертательная геометрия / Методичка для выполнения задания

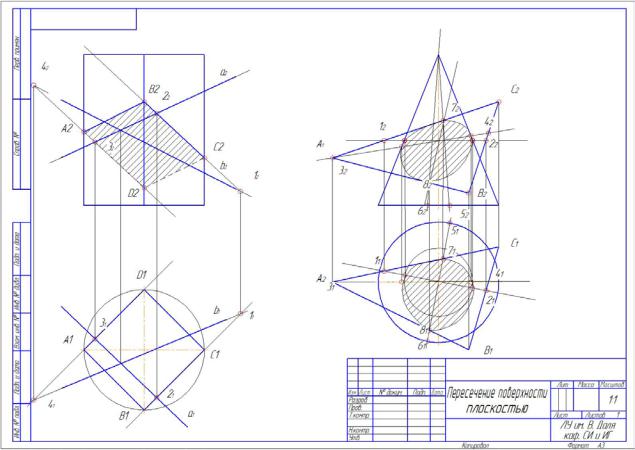
Рисунок 2.8 – Пересечение поверхности плоскостью План построения задачи 1.

1. В 1-й задаче (рис.2.9) дана четырехгранная пирамида SABCD, пересекаемая плоскостью, заданной треугольником MNP. Две проекции пирамиды и плоскости строятся согласно варианту задания, а третья проекция - по 2-м заданным.

Для определения фигуры сечения пирамиды плоскостью MPN применяем вспомогательные плоскости-посредники.

Результатом пересечения четырехгранной пирамиды с плоскостью может быть многоугольник. Определяем точки пересечения пирамиды SABCD плоскостью. Для определения точки на ребре SC заключаем ребро SC в горизонтально-проецирующую плоскость Σ. Она рассекает пирамиду по ∆ASC, а плоскость MNP по прямой 1-2. Пересечение 12-22 с треугольником A2S2C2 дает нам 2 точки - К и L. Точка К принадлежит ребру SA. Для определения точек на ребрах SD и SB проводим в плоскостях ASB и ASD

21

вспомогательные прямые S3 и S37 и находим точки пересечения этих прямых с плоскостью MNP, заключая S3 и S3' во фронтально-проецирующую плоскость ∆2. Получив точки пересечения прямой S3 и S3' с плоскостью мы видим, что ребро SB в пересечении не участвует. Соединив К и Е до пересечения с ребром SD получаем точку F.

Дляопределенияточеквплоскостиоснованиявводимвспомогательную плоскость-посредник T2 через фронтальную проекцию основания пирамиды

ABCD.

Плоскость T2 пересекает пирамиду по четырехугольнику ABCD, а плоскость MNP пo линии 61-71. Пересечение A1В1C1D1 с 61-71 дает нам точки G1 и R1. Точки G2 и R2 находим, проведя линии связи. Соединяя полученные точки получаем многоугольник GКFLR. Видимость его сторон определяем по методу конкурирующих точек.

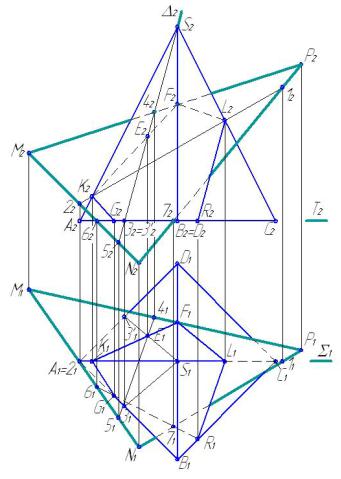
Рисунок2.9 – Сечение, образуемое пересечениемплоскостью пирамиды

22

2. Во второй задаче дан конус. Построение сечения начинаем с опорных точек.

Опорные точки K и L найдем с помощью фронтальной плоскости ∆1, проведенной через ось конуса. Эта плоскость рассечет конус по крайним образующим SA и SB, а плоскость ∑ - по ее фронтали. На пересечении фронтали с крайними образующими находим точки K и L,в которых эллипс сечения прикасается к этим образующим. Далее проводим через ось конуса плоскость θ, перпендикулярную к секущей плоскости (след θ1 h1°). Плоскость θ пересекает поверхность конуса по образующим SC и SД, а плоскость ∑-по прямой 2-3, являющейся линией наибольшего наклона плоскости∑кплоскостиП1. На этой прямой находятся точкиM иN, в которых образующие конуса SC и SД соответственно пересекут плоскость ∑. Причем точка M- высшая, а точка N- низшая из всех точек, принадлежащих сечению конуса плоскостью ∑. Ряд других точек эллипса можно построить или при помощи горизонтально - проецирующих плоскостей, проведенных через вершину S конуса, или при помощи горизонтальных плоскостей. Точки E и F эллипса получены путем проведения вспомогательной горизонтальной плоскости Ω. Плоскость Ω пересекает плоскость ∑ по горизонтали, а конус по окружности, диаметр которой равен отрезку следа Ω2, заключенному между фронтальными проекциями S2A2 и S2B2 крайних образующих конуса. Проводя эту окружность из центра S1, получаем в ее пересечении с горизонтальной проекциейгоризонталиточкиE1 иF1,покоторымнайдетточкиE2 иF2 наследе Ω2 плоскости Ω с помощью линий связи. Соединяя точки K1, M1, F1, L1, N1, E1 и K1 плавной кривой, получаем эллипс, являющийся горизонтальной проекцией сечения конуса плоскостью ∑. Фронтальная проекция сечения – также эллипс, проходящий через точки K2, M2, F2, L2, N2, E2 и K2.

23

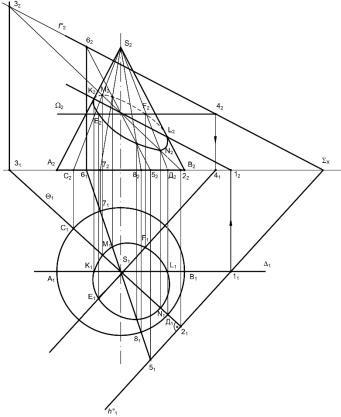
Рисунок 2.10 - Сечение, образуемое пересечением плоскостью конуса Содержание

2.5 Лист 5 Построение и исследование тела вращения

На формате А3 в масштабе 1:1 выполнить построение трёх проекций тела вращения и аксонометрическое изображение данного тела вращения.

Исходные данные для выполнения задания: даны горизонтальная и фронтальная проекции тела вращения (цилиндр или конус). Из тела вращения вырезана призматическая часть объёма, образованная плоскостями частного положения. Необходимо выполнить построение профильной проекции тела вращения и построить указанный вырез на трёх проекциях. При построении невидимые линии указываются штриховой линией.

Размеры для построения: высота тела вращения - 100 мм, диаметр основания 80 мм.

Пример построения листа 5 показан на рис.2.11.

24

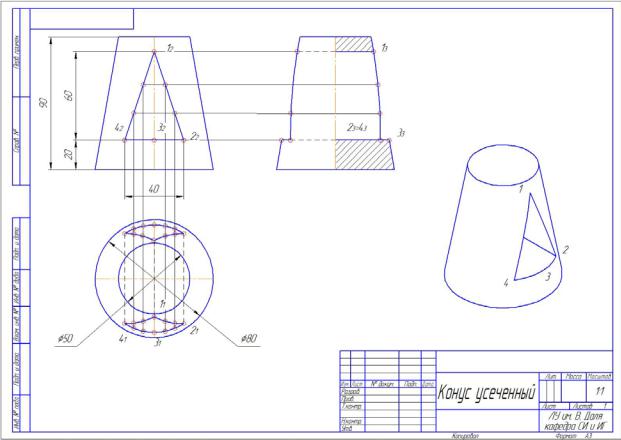
Рисунок 2.11 – Конус усеченный

Проекции отверстия строим следующим образом:

Фронтальная проекция сквозного отверстия совпадает с его следомпроекциейнаплоскостиП2,таккакданноеотверстиезанимаетпроецирующее положение относительно этой плоскости проекций. При этом грани призматического отверстия пересекают конус по кривым 2-го порядка - эллипсам, поэтому для построения горизонтальной проекции используем вспомогательные плоскости Σ, Q, ∆, Θ и Т горизонтального уровня, которые пересекают конус по окружностям, а фронтально - проецирующее отверстие - по прямым линиям. Вспомогательные плоскости целесообразно провести через точки Р, К, D, М призматического отверстия. Необходимо также несколько плоскостей для получения промежуточных точек фигуры сечения.

Например, плоскость горизонтального уровня Q пересекает конус по окружности соответствующего радиуса, а призматическое отверстие - по

прямым 11' и 22'. Проводим на горизонтальной проекции окружность 6 и

25

определяем точки пересечения ее с указанными прямыми (фактически проводим линии связи из точек 12 = 12' и 22 = 22' на плоскость П1) в точках 11, 11', 21', 21, которые являются точками контура отверстия на горизонтальной проекции. После получения достаточного количества точек соединяем их плавными кривыми и получаем горизонтальную проекцию сквозного отверстия конуса.

Профильную проекцию отверстия строим по линиям связи. Содержание

2. 6 Лист 6 Построение и исследование многогранника

На формате А3 в масштабе 1:1 выполнить построение трёх проекций многогранника и аксонометрическое изображение данного многогранника.

Исходные данные для выполнения задания: даны горизонтальная и фронтальная проекции многогранника (призмы или пирамиды). Из тела многогранника вырезана призматическая часть объёма, образованная плоскостями частного положения. Необходимо выполнить построение профильной проекции многогранника и построить указанный вырез на трёх проекциях. При построении невидимые линии указываются штриховой линией.

Размеры для построения: высота многогранника - 100 мм, диаметр описанного основания 80 мм.

Пример построения листа 6 показан на рис. 2.12.

26

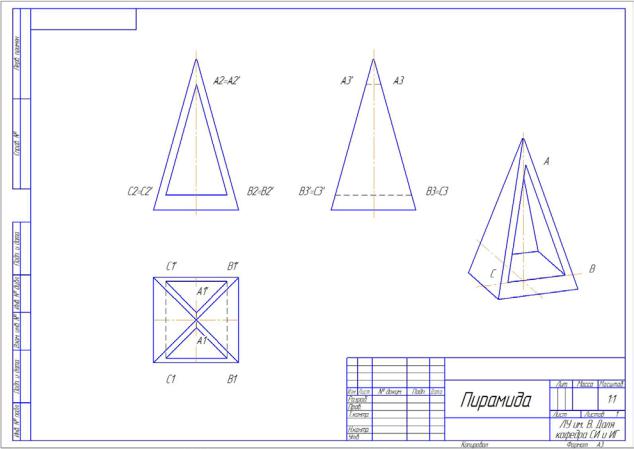
Рисунок 2.12 – Пирамида

Содержание

2.7 Лист 7 Исследование пересечения многогранников

На формате А3 построить линию пересечения двух многогранников. Невидимыелинииуказатьштриховойлинией.Дляпостроениявыбратьвысоту многогранника100 мм, диаметр описанного основания 80 мм.

Пример построения показан на рис. 2.13.

План построения линии пересечения пирамиды с прямой призмой.

-согласно своему варианту взять координаты точек А, В. С и Q вершин пирамиды и координаты точек Е, К, G, U вершин многоугольника нижнего основания призмы, а также высоту h призмы:

-по этим данным построить проекции многогранников (пирамиды

ипризмы);

-призма своим основанием стоит на горизонтальной плоскости проекций, поэтому горизонтальные проекции ее вертикальных ребер

27

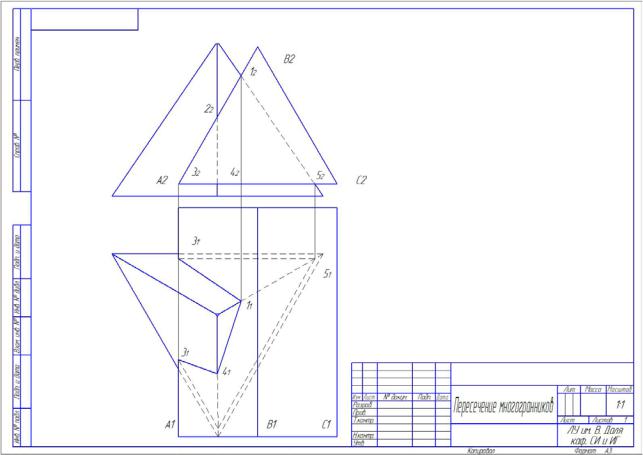
проецируются в точки, грани же боковой поверхности представляют собой горизонтально проецирующие плоскости;

Рисунок 2.13 – Пересечение многогранников

-линии пересечения многогранников определить по точкам пересечения ребер каждого из них с гранями другого многогранника или построением линии пересечения граней многогранников;

-соединив пары точек, принадлежащих одним и тем же граням, отрезками прямых получим линию пересечения многогранников;

-определить видимость граней многогранников и отрезков линии пересечения способом конкурирующих точек или, учитывая, что видимыми являются только те отрезки линии пересечения, которые принадлежат видимым граням многогранников;

-видимые грани и отрезки линии пересечения показать сплошными толстыми (основными) линиями, а невидимые - штриховыми;

28

Список литературы

1.Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии /В.О. Гордон, М.А. Семенцов-Огиевский М., 2006. 272с.

2.Фролов С.А. Начертательная геометрия /С.А. Фролов М.: Высшая школа, 2002. 240 с.

3.Начертательнаягеометрия(ЧетверухинН.Ф.,ЛевицкийВ.С.идр.)М.,

1973 г.

4.Хаскин А.М. Черчение, К.: Вища школа, 1986. – 446 с.

5.Фролов С.А. Сборник задач по начертательной геометрии, М.: Машиностроение, 1980. 142 с.

6.Чекмарев А. А. Справочник по машиностроительному черчению /А. А. Чекмарев, В.К. Осипов. М.: Высшая школа, 2007. 493 с.

7.Локтев О. В. Краткий курс начертательной геометрии /О.В. Локтев. М.: Высшая школа, 2004. 136 с.

8.Чекмарев А. А. Начертательная геометрия. Инженерная и машинная графика /А. А. Чекмарев. М.: Высшая школа, 2006. 155 с.

9.Савельев Ю. Ф. Начертательная геометрия /Ю.Ф. Савельев / Омский гос. ун-т путей сообщения. Омск, 2005. 43 с.

10.Нартова Л. Г. Начертательная геометрия /Л.Г. Нартова, В. И., Якунин. М.: Академия, 2005. 288 с.

Содержание

29

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ИУЧЕБНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ

«НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ, ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА»

(для студентов всех специальностей)

Составители:

Анатолий Григорьевич МАКУХИН, Геннадий Владимирович СЫРОВОЙ

Подписано в печать __ . __ . 10

Формат 60х84 1/16. Бумага офсетная. Гарнитура Times. Печать офсетная. Усл.печ.л.___. Усл. кр.-отт.___. Уч.-изд.л. ___

Тираж 200. Издат. №____ Заказ №______ Цена договорная.

Издательство Луганского государственного университета

Имени Владимира Даля 91034, г. Луганск, кв.Молодежный, 20а

Адрес редакции: 91034, г.Луганск, кв.Молодежный, 20а

Телефон: 8 (0642) 41-34-12. Факс: 8 (0642) 41-31-60 E-mail: kafedraf@i.ua.

http: www. dahluniver.ru/ 30