Индекс Ласпейреса

Формула агрегатного индекса цен Ласпейреса в контрольных по статистикепо индексам цен рассчитывается как отношение:

Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по продукции, которая была реализована в базисном периоде, и экономию (перерасход), который можно было бы получить от изменения цен. Индекс цен Ласпейреса также показывает, во сколько раз товары базисного периода подорожали (подешевели) в результате изменения цен на них в отчетном периоде.

Индекс Фишера

Американский экономист И. Фишер предложил «идеальный» индекс цен, который назвали его именем, представляющий собой среднюю геометрическую произведения двух агрегатных индексов цен Ласпейреса и Пааше.

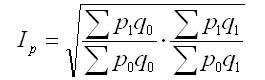
Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т. е. при перестановке базисного и отчетного периодов полученный обратный индекс представляет собой величину, обратную величине первоначального индекса. Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).

Средний гармонический индекс цен

Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.

Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:

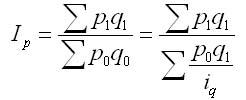
Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.

Средний арифметический индекс цен

Средний арифметический индекс цен получают в том случае, если из индивидуального индекса цен ip = p1/p0 выразить цену отчетного периода p1 = i0p0, а затем подставить ее в числитель агрегатного индекса цен.

Данный индекс аналогичен агрегатному индексу Ласпейреса и имеет формулу:

В этом индексе весами осредненных индивидуальных индексов служит объем товарооборота в базисном периоде.

1. Статистика – отрасль практич. деят-ти по сбору, обработке, анализу и публикации статистич. инф-ции, как в целом по стране, так и по отдел. ее регионам. Она изучает количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной или их содержанием, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени.

2. Этапы статистического исследования: 1) этап сбора первич. статист. материала, проверки его полноты и его достоверности (исп. метод смеш. и несмеш. стат. наблюдения), 2) этап обработки данных, подсчета групповых и общих итогов, просчета некоторых относит. показателей (исп. метод группировок), 3) этап расчета и интерпретации обобщ. стат. показателей, получ. результаты подверг. анализу, 4) этап моделирования взаимосвязей между социал.-экономич. процессами и явлениями (исп. метод построения уравнений регрессии и трендовых моделей).

3. Статистическое наблюдение – это массовое планомерное наблюдение за соц.-экономич. явлениями и прцессами, кот. заключается в регистрации необход. признаков по каждой единице изучаемой совокупности. Стат. наб-ние носит массовый хар-р, т.к. при наб-нии необх-мо получ. данные от максим. числа изуч. единиц совокупности. В наст. время в стат-ке сущ. 3 основ. формы стат. наб-ния: - отчетность, - спец. организов. стат. наб-ние, - регистры.

4. Люб. стат. исследование необх. нач. с точной формулировки его цели, конкрет. задач и сведений, кот. могут быть получены в процессе наблюдения. В программно-методических вопросах стат. наб-ия определ. объект (совокупность соц.-эконом. явлений и процессов, кот. подлежат исследованию, или точные границы, в пределах кот. будут регист-ся стат. сведения) и единица наблюдения (состав. часть объекта наблюдения, кот. служит основой счета и обладает признаками, подлежащ. рег-ции при наблюдении), разрабатыв. программа, выбираются вид и способ наблюдения. Программа наб-ния – это пречень вопросов, по кот. собир. сведения, либо перечень признаков и показателей, подлеж. рег-ции. Программа наб-ния оформляется в виде бланка (анкеты, формуляра), в кот. занос. первич. сведения. К бланку прилог. инструкция, разъясн. смысл вопросов. Состав и содерж. вопросов программы наб-ния зависит от задач исследования и от особенностей изуч. общственного явления.

5. Люб. стат. исследование необх. нач. с точной формулировки его цели, конкрет. задач и сведений, кот. могут быть получены в процессе наблюдения. В организационных вопросах стат. наб-ия определ. субъекта (орган, осуществл. набл-ние), места, времени (период, срок или объективное время набл-ния), формы и способа наблюдения. Момент времени, к кот. приурочены регистр. сведения, назыв. критич. моментом. набл-ния. Устанавл. Крит. момент, можно с фотографич. точностью отразить истинное состояние явления в данный момент.

6. Стат. сводка – это науч. обраб-ка первич. данных с целью получ. обобщ. хар-тик изуч. соц.-эконом. явления по ряду сущ-ных для него признаков. Целью стат. сводки явл. выявление типич. черт и закономерностей присущих изуч. явлению в целом. Стат. сводка быв.: - простой и сложной (по глубине и точности обр-ки), - централизованной и децентрализованной (по форме обр-ки материала). Стат. группировка – это разбиение общей совокуп-ти единиц объекта набл-ния по одному или нескольким существ. признакам на однород. группы. Стат. груп-ки быв.: - типологические, структурные и аналитические (по типу поставленной задачи), - простые и сложные (по способу построения).

7. Абсолютные стат. величины – это стат. показатель, харак-щий абсолют. размеры изуч. стат-кой процессов и явлений, а именно их массу, объем, площадь, протяженность, времен. хар-ки. Виды: -индивид. абсолют. пок-ль (получ. в процессе стат. наб-ния, как результат замера, взвешивания, подсчета, оценки колич. признака), - свобный абсолют. пок-ль (получ. в результате сводке групп-ки индивид. значений). Абсолют. стат. пок-ль всегда явл. наименованным числом. В зависимости от соц.-эконом. сущности исслед-мых физ. свойств абсолют. стат. пок-ль выраж. в: - натур. единицах (кг., кв.м., галлоны, шт. и др.), - стоимостных ед. (денеж. выражение), - трудовых ед. (человекодни, человекочасы и т.п.).

8. Относительные стат. величины – это результат деления одного абсолютного стат. показателя на другой, и выражается соотношением между количеств. харак-ками соц.-экономич. процессов и явлений. При расчете относит. пок-ля абсолют. пок-ль нах. в числителе, а получ. отношение назыв. текущим или сравнительным. Относит. пок-ли выраж. в коэф-тах, процентах или быть наименован. числами. Виды: - относ. пок-ль динамики, - -//- плана, - -//- реализации плана, - -//- структуры, - -//- координации, - -//- интенсивности и уровня экономич. развития, - -//- сравнения.

9. Средние величины – это наиболее распростран. форма стат. показателей, исп. в экономич. исследованиях. Сред. величины представл. собой обобщ. колич. хар-ку признаков в стат. совокуп-ти в конкрет. условиях, месте и времени. От того в каком виде представл. исход. данные для расчета сред. пок-ля зависит каким образом будет реализовано его исход. соотношение. Таким образом различают след. виды средних величин: - сред. арифметическая, - сред. гармоническая, - сред. геометрическая, - сред. квадратическая (кубическая).

10. Все сред. величины в зависимости от хар-ра имеющ. данных могут быть простыми или взвешенными (эта форма исп. в тех случаях, когда расчет ведется по на сгрупиров. данным). Сред. арифметическая простая: где n – число наблюдений, Xi – i-ый вариант осредненного признака, Fi – весь i-ый вариант. Сред. арифметическая взвешанная, сред. гармоническая простая, сред. гармоническая взвешенная: где Wi = Xi*Fi

11. Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет: 1) величина средней ариф. на изменится, если веса всех вариантов умножить или разделить на одно и тоже число (исп. для расчетасред. значений через показатели структуры), 2) если все индивидуальные значения признака (т.е. все варианты) увеличить либо уменьшить в одно и то же число раз (или на одо и то же число), то сред. значения получившегося нового признака будет во столько же раз (или на столько же) отличаться от среднего значения исходного показателя (исп. ускорения расчетов, особенно если первич. данные представлены в сгруппированном виде).

12. Вариация стат. пок-ля признака, изучаемых объектов – это несовпадения уровней одного и того же показателя у разных объектов, она им. объяктив. хар-р и помогает познать сущность изучаемого явления. Расчет пок-ля размаха вариации:

Н=X_max - X_min. Повторяемость промеж. знач. в пок-ле размаха вариации Н не учитываются. Расчет среднего линейного отклонения:

При повторяемости отдел. значений Х используют формулу сред. ариф. взвешанной:

Расчет показателя дисперсии:

Пок-ль, равный, назыв. сред. квадратическим отклонением.

13. Стат. индекс – относит. величина сравнения слож. совокупностей и отдельных их единиц. В экономич. анализе индексы использ. не только для сопоставления уровней изуч. явления, но и для определения экономич. значимости причин, объесн. абсолют. различие сравниваемых уровней. В завис. от сложности сравнив. уровней сущ. 3 вида: - индивидуальные инд-сы, - общие инд-сы, - инд-сы сред. величин. Индивидуальные инд-сы хар-ют изменения отдельных единиц совокупности. Индивид. инд-сы физич. объема реализации товаров определ. по формуле:

где- кол-во продажи отдельной товар. разновидности текущ. и базисном периодах в натур. измерителях.

Индивид. инд-сы цен:

где- цены за единицу товара в текущ. и базисном периодах

Индивид. инд-сы прироста товараоборота:

14. Общие стат. индексы могут исчисляться как по агрегатной,так и по средней форме (сред. арифметич. или сред. гармонического индекса) Выбор формы общих инд-совзавис. от хар-ра исход. данных. Основ. формой общих инд-сов явл. агрегатные индексы. Расчет агрегат. инд-са цен (Индекс Пааше) вед. по формуле:

где- кол-во продажи отдельной товар. разновидности текущ. и базисном периодах в натур. измерителях,- цены за единицу товара в текущ. и базисном периодах

Общий индекс физического объема товарооборота определ. по формуле:

Индексы связаны между собой и представляют индексную факторную модель, кот. позволяет разложить индекс товарооборота по факторам:

Общий абсолют. прирост товарооборота, перставл. аддитивной моделью(аддитивный - суммарный уровень):

∆∑pq = ∆∑pq (p) + ∆∑pq (q)

15. Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.

сред. арифметическая физ. объема:

Сред. гармоническая физ. объема:

16. Выборочный метод наблюдения применяется в тех случаях, когда проведение сплошного набл-ния невозможно или экономич. нецелесообразно. Оно исп. также для проверки результатов сплошного наблюдения. Часть единиц, отбранных для набл-ния назыв. выборочной совокупностью, а всю совокупность единиц, из кот. производится отбор – генеральной. Сущ. след. способы формирования выборочной совокупности: индивидуальны, случайный, механический, стратифицированный, серийный отбор. Особенности обследуемых объектов определ. 2 метода отбора единиц в выбороч. совокупность: повторный (отбор по схеме возвра- щенного шара), бесповторный (отбор по схеме невозвращенного шара). Бесповторный отбор дает более точные результаты по сравнению и повторным, так как при одном и том же объеме выборки наблюдение охват. больше единиц генеральной совокупности.

17. Разность между показателями выборочной и генеральной совокупности назыв. ошибкой выборки. Сущ. средняя и предельная ошибка выборки, кот. исчесл. для количественных и качественных признаков. Наиболее частой ошибкой явл. отождествление 1) средней ошибки выбороч. средней (количеств. признак) и 2) средней ошибки выбороч. доли (качеств. признак).

1) для повторного отбора:

для бесповторного отбора:

где - дисперсия признака,

- числ. выбороч. совокупности

- числ. генеральной совокупности.

2) для повторного отбора:

для бесповторного отбора:

где w = m / n

18. Формулы для определения численности выборки зависят от метода отбора. Они различны для расчета средней и доли.

Повторный метод отбора:

для средней

для доли

Бесповторный метод отбора:

для средней

для доли

При отборе с учетом вариации признака расчет числ. выборки произв. по формулам:

для средней

для доли

19. Ряд динамики – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включ.: время и конкретное значение показателя, или уровень ряда. Ряды динамики по времени различают: - моментные (ряды динамики отображают сост. изуч. явлений на определ. даты (моменты) времени), - интервальные (ряды динамики отображ. итоги развития 9функционирования) изуч. явлений за отдел. периоды (интервалы) времени). При изучении явления во времени необходимо описать интенсивность изменения и рассчитать сред. показатели динамики. Для этого сущ.след. показатели: абсолютный прирост, темпы роста, темпы прироста, абсолют значение одного процента прироста.

20. Система средних показателей динамики вкл.: - средний уровень ряда

(для равного периода времени)

где n или (n +1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi (1 = 1, 2, ..., n или 1 = 0, 1, 2, ..., n).

- средний абсолют. прирост рассчитывается по формулам в зависимости от способа нумерации интервалов (моментов). .

- средний темп роста

где – средний коэффициент роста, рассчитанный как. Здесь Кцеп – цепные коэффициенты роста;

- средний темп прироста (%) определяется по единственной методологии:

21. При анализе рядов динамики наиболее важной и сущ-ной задачей является определение основной тенденции развития, присущей тому или иному ряду динамики. Существует две основ. группы стат. методов анализа основной тенденции в рядах динамики: - сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактич. значений сосед. уровней, - выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду и одновременно освободила его от незначит. колебаний. К этим группам относятся методы: - метод укрупнения интервалов, - метод простой скользящей средней, - центрирование.

22. Под взаимосвязанными понимаются такие ряды динамики, в кот. уровни одного ряда в какой-то степени определ. уровни другого. В простейших случаях для хар-ки взаимосвязей двух и более рядов их приводят к общему основанию, для чего берут в качестве базисных уровни за один и тот же период и делают расчеты. Формы проявления взаимосвязей разнообразны. В кач-ве двух общих их видов выдел.: - функциональную (полную) связь, в кот. величина факторного признака строго соответствует одно или несколько значений функции, - корреляционную (неполную или статистическую) связь, кот. проявляется для массовых наблюдений, когда заданным значениям зависимой переменной соотв. некоторый ряд вероятных значений независимой переменной. Классифицир. они след. образом: - по направлению связи (прямые и обратные), - по кол-ву признаков в связи ( парная и множественная), - по силе (слабые и сильные), - а так же косвенные, непосредственные и ложные связи.

23. Тренд – основная тенденция развития динамич. ряда (к увеличению или снижению его уровней). Расчете тренда включ. два основ. этапа: - на первом ряд динамики проверяется на наличие тренда, - на втором – производится выравнивание временного ряда и непосредственное выделение тренда с анализом полученный результатов. При проверке на наличие тренда в ряду динамики исп.: - метод средних, - фазочастотный критерий знаков первой разности (Валлиса и Мура), - критерий Кокса и Стюарта, - метод серий.

24. На практике для количественной оценки тесноты связи широко используется линейный коэффициент корреляции. Если заданы значения переменных X и Y, то он вычисл. по формуле:

Коэф-нт корреляции принимает значения в интервале от -1 до +1. Принято счетать, что если /r/< 0,30, то связь слабая; при /r/=(0,3÷0,7) – средняя; при /r/>0,70 – сильная или тесная; когда /r/=1 – связь функциональная; если же r≈0, то это дает основание судить об отсутствии линейной связи между X и Y.

25. Для хар-ки влияния изменений одной вариации на другую вариацию служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель:

Yi = a₀ + a₁ * Xi + ε_i

i = 1, …, n,

где n – число наблюдений, a₀ и a₁ – неизвестные парметры уравнения, ε_i - ошибка случайной переменной Y.

26. Система национальных счетов - система национального учета, основанная на обобщении и систематизации данных сплошных и выборочных обследований, а также статистической отчетности. Результатом обработки первичной информации является комплекс балансовых таблиц, показатели которых позволяют определить обобщающие макроэкономические показатели, характеризующие состояние экономики и динамику экономического роста. Основными экономич. хар-ками в СНС выступают валовой внутр. продукт и валовой национальный продукт. В СНС используется система двойной записи по методу бухгалтерского учета. В практике российской статистики показатели СНС впервые были рассчитаны в 1988 г.

27. Оснв. структурными элементами системы национальных счетов явл: 1) экономические функции - производство, потребление, накопление, посредничество в перераспределении доходов; 2) экономические операции - операции с материальными благами и услугами, операции по распределению, финансовые операции и пр.; 3) экономические агенты - субъекты экономических операций, принимающие хозяйственные решения (чистые отрасли, институциональные секторы); 4) объекты экономических операций - товары, услуги, деньги, финансовые документы. Метод построения системы национальных счетов заключается в отражении всех экономич. процессов как совокупности двусторонних операций, совершаемых контрагентами. Национальное хоз-во представляется в виде замкнутой модели; экономическая деят-ть субъектов расписывается по счетам как потоки доходов и расходов.

28. Система национальных счетов представляет собой совокупность стат-ких макроэкономических показателей, харак-ющих величину совокупного продукта (выпуска) и совокупного дохода, позволяющих оценить состояние национальной экономики. СНС содержит три основных показателя совокупного выпуска (объема производства): валовой национальный продукт (ВНП), валовой внутренний продукт (ВВП); чистый национальный продукт (ЧНП), и три показателя совокупного дохода: национальный доход (НД); личный доход (ЛД); располагаемый личный доход (РЛД). Стандартная система национальных счетов разработана статистической комиссией ООН в 1953 г

29. Валовой внутренний продукт - совокупная стоимость всех товаров и услуг, произведенных в течение года на территории страны без разделения ресурсов, использованных на их производство, на импортные и внутренние. Для большинства стран мира показатели ВВП и ВНП различаются незначительно и зачастую счит. взаимозаменяемыми. Чаще всего используют два метода расчета ВВП: -1- путем суммирования всех доходов в экономике: заработной платы, процентов на капитал, прибыли и ренты; -2- путем суммирования всех произведенных расходов: потребления, инвестиций, госуд-ных закупок товаров и услуг, а также чистого экспорта. Теоретически результаты вычислений в обоих случаях должны совпадать, поскольку расходы одного участника экономических отношений всегда являются доходами для другого.