9. Графическое изображение вариационных рядов. Полигон и гистограмма.
Одним из этапов изучения вариационного ряда является его графическое изображение. Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигон распределения частот и гистограмма частот.
Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаково масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот.
Для построения гистограммы по оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат.
10. Основные характеристики вариационных рядов. Показатели центра распределения.
Исчисление основных характеристик распределения происходит по 3 группам показателей: 1. центра распределения; 2. степени вариации; 3. формы распределения.
Для характеристики центра распределения в вариационном ряду применяются: средняя арифметическая, медиана, мода.
Средняя арифметическая для дискретного ряда распределения исчисляется по формуле:
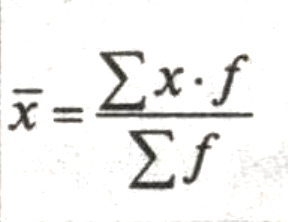
где x - варианты значений признака; f- частота повторения данного варианта.
Средняя арифметическая для интервального ряда распределения:
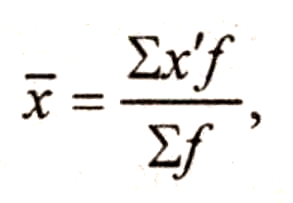
где х' — середина соответствующего интервала значения признака; вычисляется как средняя из значений границ интервала.
Структурные средние – мода и медиана – в отличие от степенных выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решения ряда практических задач.
Модой (Мо) называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Медианой (Ме) называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
11. Показатели вариации ряда распределения. Дисперсия; коэффициент вариации.
Показателями степени вариации бывают абсолютные: размах колебаний, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия; и относительными: коэффициент вариации.
Дисперсия исчисляет так:
Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному)
