Экзамен Физика 2 семетр / Lekcii_po_fizike_(Bogdanov)

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 16.7

 Поле равномерно заряженной плоскости.

Пусть поверхностная плотность заряда равна σ. Из симметрии задачи, очевидно, что вектор Е может быть только перпендикулярным заряженной плоскости. Кроме того, ясно, что в симметричных относительно этой плоскости точках вектор Е одинаков по модулю и противоположен по направлению. Такая конфигурация поля подсказывает, что в качестве замкнутой поверхности следует выбрать прямой цилиндр с основаниями параллельными плоскости.

Поток сквозь боковую поверхность этого цилиндра равен нулю, и поэтому полный поток через всю поверхность цилиндра будет 2EΔS, где ΔS – площадь каждого торца цилиндра. Внутри цилиндра заключен заряд σΔS. Согласно теореме Гаусса 2EΔS= σΔS откуда

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 16.8

 Поле бесконечного круглого цилиндра Поле бесконечного круглого цилиндра,

заряженного равномерно по поверхности так, что на единицу его длины приходится заряд λ. Из соображений симметрии следует, что вектор Е в каждой точке перпендикулярен оси цилиндра, а модуль вектора Е зависит только от расстояния r до оси цилиндра. Это подсказывает, что замкнутую поверхность надо взять в форме коаксиального прямого цилиндра.

Тогда поток вектора Е сквозь торцы этого цилиндра равен нулю, а через боковую поверхность ЕΔS, где ΔS – площадь боковой поверхности цилиндра ΔS=2πrh. r – радиус боковой поверхности цилиндра, h – его высота. По теореме Гаусса для случая r>R (R – радиус бесконечного круглого цилиндра) имеем Е2πrh= λh/ε0, откуда:

E

2 0r

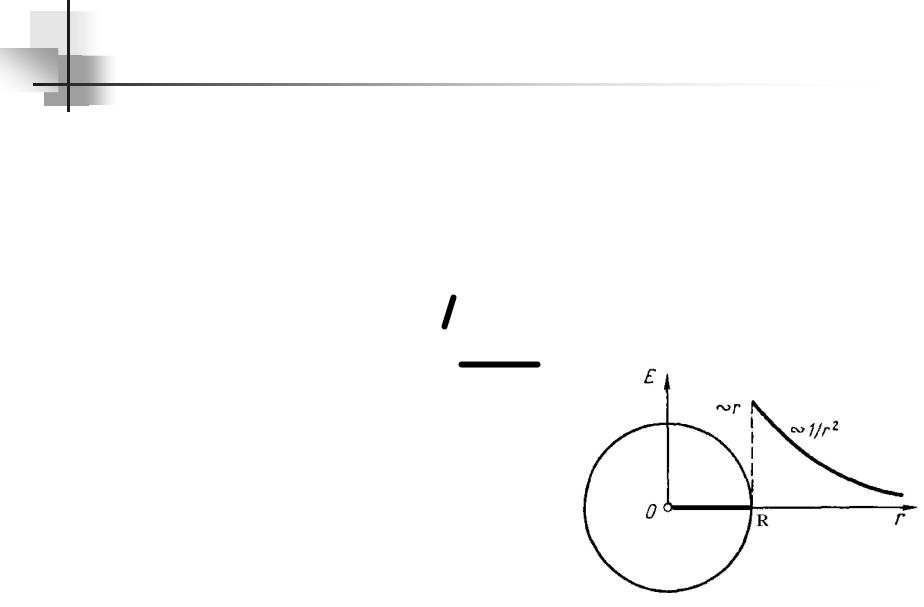
Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 16.9

 Поле сферической поверхности, заряженной равномерно зарядом q.

Это поле центрально-симметрично – направление вектора Е в любой точке проходит через центр сферы, а модуль зависит только от расстояния до центра сферы. При такой конфигурации поля в качестве замкнутой поверхности надо взять концентрическую сферу. Пусть ее радиус r>R,

тогда по теореме Гаусса E 4 r2 q откуда

0

E

q

4 0r2

Если r<R, то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду Е=0, т.е. внутри равномерно заряженной сферической поверхности электрическое поле отсутствует. Вне этой поверхности поле убывает с расстоянием по такому же закону, как у точечного заряда.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 16.10

 Поле сферы заряженной объемной плотностью заряда ρ

Поле такой сферы тоже обладает центральной симметрией. Для поля вне сферы получается тот же результат, что и в случае поверхностно заряженной сферы. Однако для точек внутри результат будет другой. Сферическая поверхность радиуса r (r<R) заключает в себя заряд равный 4 r3

3

Следовательно, теорема Гаусса для такой поверхности запишется в виде:

E 4 r2 1 4 r3

Внутри сферы напряженность поля растет линейно с расстоянием r от центра сферы. Вне сферы напряженность убывает по такому же закону, как и у точечного заряда.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 17.2

Интеграл данного вида, взятый по замкнутому пути, называется циркуляцией вектора Е и обозначается С

Теорема о циркуляции вектора Е гласит:

циркуляция вектора Е в любом электростатическом поле равна нулю т.е.

2

Edl 0

1

Поле, обладающее таким свойством, называется потенциальным. Теорема о циркуляции вектора Е позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Например, линии электростатического поля не могут быть замкнутыми.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 17.3

Тело находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа сил электростатического поля может быть представлена как разность значений потенциальной энергии, которыми обладал заряд в точках 1 и 2 поля Е. Можно утверждать, что в электростатическом поле существует некоторая скалярная функция координат φ(r), убыль которой

2

1 2 Edl

1

Так определенная величина φ(r) называется потенциалом поля.

Из сопоставления данного выражения с выражением для работы сил потенциального поля ( которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 17.4

Потенциал какой-либо произвольной точки поля определяется с точностью до произвольной аддитивной константы.

Элементарная убыль потенциала на dl есть

d Edl

Другими словами, если известно поле E(r), то для нахождения φ надо представить как убыль некоторой функции.

Потенциал поля неподвижного точечного заряда:

Таким образом, потенциал поля точечного заряда

1 q 4 0 r

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 17.5

Если имеется система из N неподвижных точечных зарядов q1, q2, …. Согласно принципу суперпозиции в любой точке поля напряженность Е=Е1+Е2+…, где Еi – напряженность поля создаваемого отдельно зарядом q1 и т.д. Тогда можно записать

Edl (E1 E 2 ....)dl E1dl E2dl .... d 1 d 1 ... d

Таким образом, потенциал системы неподвижных точечных зарядов

Если заряды, образующие системы, распределены непрерывно, то, каждый элементарный объем dV содержит точечный заряд ρdV, где ρ – объемная плотность заряда в месте нахождения объема dV. Тогда при вычислении потенциала можно перейти от суммирования дискретно распределенных в пространстве зарядов к интегрированию по

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Электростатика. 17.6

Если заряды расположены только по поверхности S то получаем

Получили, что электрическое поле можно описывать как с помощью напряженности, так и с помощью потенциала. Следовательно, раз эти две величины описывают одно и то же физическое явление, то между ними должна существовать однозначная связь.

Связь между φ и Е можно установить с помощью соотношения d Edl

Пусть перемещение dl параллельно оси Х, тогда dl=exdx, где ex – орт оси Х; dx – приращение координаты х. В этом случае

Edl Eexdx Ex dx