Soprotivlenie_materialov / 270800_62 (ПГС)-10-1234-2428 / 04. Конспект лекций

73

Вопросы для самопроверки

1.Какой изгиб называется косым?

2.Сочетанием каких видов изгиба является косой изгиб?

3.По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

4.Как находится положение нейтральной оси при косом изгибе?

5.Как определяются опасные точки в сечении при косом изгибе?

6.Как определяются перемещения точек оси балки при косом изгибе?

7.Какой вид сложного сопротивления называется внецентренным растяжением (или сжатием)?

8.По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений?

9.Как определяется положение нейтральной оси при внецентренном растяжении и сжатии? Запишите соответствующие формулы.

10.Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

11.Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

12.Какие точки круглого поперечного сечения являются опасными при изгибе с кручением?

13.Какое напряженное состояние возникает в этих точках?

74

ТЕМА 9. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ Вопросы :

1.Понятие об устойчивости. Задача Эйлера.

2.Влияние способов закрепления концов стержня на критическую силу.

3.Пределы применимости формулы Эйлера.

4.Расчет стержней на устойчивость по коэффициенту продольного изгиба.

9.1 Понятие об устойчивости. Задача Эйлера

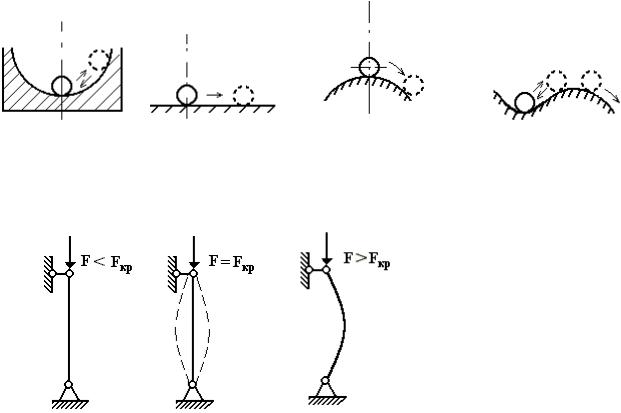
Из теоретической механики известно, что равновесие абсолютно твердого тела может быть устойчивым (рис. 9.1,а) безразличным (рис. 9.1,б) и неустойчивым (рис 9.1,в и г).

Рис. 9.1

Равновесное состояние деформируемой системы, например, стержня также может быть устойчивым (рис. 9.2,а), безразличным (критическим) (рис. 9.2,б) и неустойчивым (рис. 9.2,в).

Строгое определение устойчивости по теореме Пуанкаре звучит так.

Пусть идеально прямой стержень нагружен строго центральной продольной силой F Fкр (рис. 9.3). При таких предположениях прямолинейная форма

стержня всегда будет являться возможной формой равновесия. Об устойчивости этой формы равновесия стержня можно судить по реакции ее на поперечную нагрузку F1. При отсутствии силы F малая сила F1 вызывает малый прогиб стержня. При небольшой силе F положение стержня не изменится, а равновесие его сохранится устойчивым.

Равновесие стержня устойчиво, если задавшись любой величиной прогиба f 0, всегда можно указать такую конечную

75

величину возмущения 0 , что при F1 величина проги-

ба

ни в одной точке системы не достигнет величины f, тоесть будет f.

Нагрузка, при которой начальная (исходная) форма равновесия стержня перестает быть устойчивой, называется критической и обозначается Fкр. Приложение к стержню силы

F Fкр или F Fкр вызывает его продольный изгиб.

ре й у с т о й ч и в о с т и с и с т е м ы .

Внекоторых случаях при потере устойчивости, система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев, потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов.

Но потеря устойчивости упругого равновесия возможна и при других видах деформаций. Так при прямом изгибе балок направление прогиба балки может существенно отклониться от линии действия нагрузки (рис. 9.4, б), и, наконец, при действии внутреннего давления на цилиндрическую оболочку ее деформации в некоторый момент перестают быть осесимметричными, оболочка искривляется и принимает некоторую новую форму (рис. 9.4, в).

F

F

p

Рис. 9.4

Разрушение от сжимающих критических нагрузок наступает внезапно при отсутствии внешних признаков приближающей потери устойчивости. Практически мгновенно происходит изменение характера нагружения, приводящего к

77

Это и есть формула Эйлера для критической силы.

Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной

z D sin l x

9.2 Влияние способов закрепления концов стержня на критическую силу

Fкр Вывод формулы Эйлера осуществлен для бруса с шарнирно закрепленными концами. Тем не менее эта формула имеет универсальный характер, не зависит от способа закрепления бруса и через коэффициент п учитывает число полуволн синусоиды, которые укладываются на его длине. Применим, например, эту формулу для определения критической силы бруса с заделанными концами (рис. 9.6). Как видим, число полуволн изогнутой оси в этом случае п = 2 и, следовательно, критическая сила при данных опорных устройствах равна

брус изгибается не по целому числу полуволн синусоиды (рис. 9.7) - брус, защемленный одним концом и шарнирно опертый другим.

78

Из этого условия получаем

и уравнение изогнутой оси приобретает следующий вид:

Отсюда получаем следующее трансцендентное разрешающее уравнение для определения величины :

tg l l .

Наименьший корень этого уравнения определяет первую критическую силу. Это уравнение решается методом подбора или графически. Наименьший, отличный от нуля, корень этого уравнения l = 4,493 = 1,43 .

Принимая l = 1,43 , получаем следующее выражение для критической силы

Проведя подобный вывод формулы для критической силы применительно к брусу, защемленному с одной стороны (рис. 9.8), получаем следующее выражение:

Сопоставляя формулы критической силы для бруса, закрепленного различным образом, легко видеть, что все они z(x) имеют одинаковое строение. Обобщая их, запишем форму-

лу Эйлера в виде:

эффициентом приведения длины, а произведение l - приведенной длиной бруса. Случай шарнирного закрепления концов бруса называется основным. Основные случаи закрепления концов стержня и значений коэффициента приведения длины для них показаны на рис. 9.9.

Таким образом, критическая сила для любого случая закрепления бруса может быть вычислена по формуле для основного случая с заменой действительной длины бруса его приведенной длиной.

82

кр 2 E .2

Стержни одинаковых длин и с одинаковыми способами закрепления могут иметь разные гибкости в зависимости от их форм поперечного сечения. Вычис-

можно провести сравнительную оценку форм поперечных сечений стержней на способность сопротивляться потери устойчивости, так как чем больше min ,тем больше величина критической силы тем устойчивее стержень.

Таблица 9.3 Относительный радиус инерции

Из таблицы 9.3 видно, что наиболее устойчивыми являются стержни с кольцевой или коробчатой формами поперечных сечений.

Вопросы для самопроверки

1.Что означает выражение «сжатый стержень потерял устойчивость»?

2.Какая сила называется критической?

3.Почему в реальных конструкциях сжимающие стержень силы должны быть меньше критических?

4.Почему нельзя допускать потерю устойчивости элементов конструкций?

5.Запишите формулу Эйлера.

6.Как влияют условия закрепления стержня на величину критической силы?

7.Запишите формулу Эйлера с учетом условий закрепления стержня.

8.Сформулируйте условие применимости формулы Эйлера.

9.Запишите формулу Ясинского.

10.Могут ли быть такие случаи, когда сжатый стержень не будет терять устойчивость?

11.Нарисуйте график зависимости кр f ( ) .

12.Опишите в общем виде схему расчета сжатых стержней с помощью коэффициента уменьшения допускаемого напряжения.