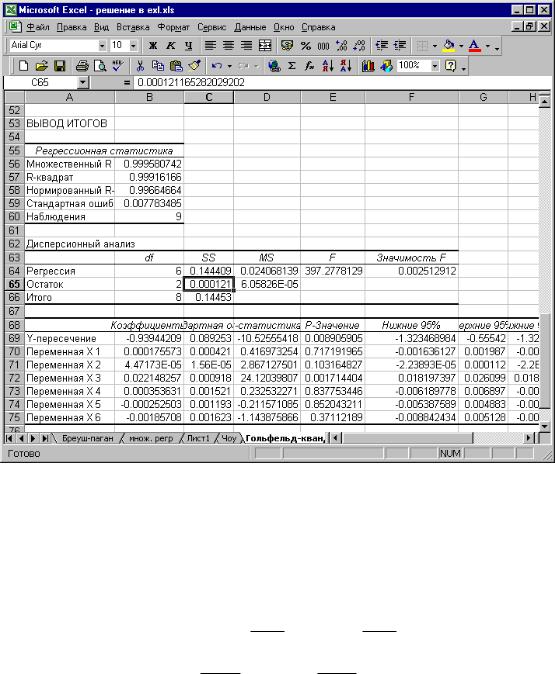
Рис. 3.16. Регрессия по последним 9 наблюдениям

Найдем статистику (3.5):

Так как

Fнабл = 0,3 < Fкрит (α;ν1 = n −2 d −k −1;ν2 = n −2 d −k −1) =

= Fкрит (0.05;ν1 = 252−7 −6 −1;ν2 = 252−7 −6 −1) =19,

то гипотеза о гомоскедастичности не отвергается.

Следует заметить, что переменная Х1 гомоскедастична, но это не значит, что по всем остальным переменным модель может быть гетероскедастичной. Поэтому необходима дальнейшая проверка по остальным переменным.

Тест Бреуша-Пагана (Breus-Pagan)

Предполагается, что дисперсия случайной ошибки зависит от

нескольких независимых переменных.

si2=γ0+γ1zi1+γ2zi2+…+γmzim.

Этапы тестирования:

1.Рассчитывают МНК-оценки коэффициентов регрессии.

2.Находят остатки ei.

3.Находят квадраты остатков ei2.

4.Рассчитывают коэффициент детерминации R2 для регрессии

6.Если X2набл превосходит критическое значение статистики Хи-квадрат для m степеней свободы, гетероскедастичность присутствует.

Задача 7

По данным таблицы 3.2 проверить гипотезу о гетероскедастичности, используя тест Бреуша-Пагана.

Решение

Рассчитаем регрессию по всем шести переменным, в результате получим регрессию (рис. 3.10). При построении регрессии необходимо вывести остатки ei, для этого следует поставить флажок «Остатки» в параметрах Регрессии (рис. 2.15).

В результате получим таблицу остатков. Найдем квадраты остатков

(рис. 3.17).

Рис. 3.17. Вывод остатка регрессии

Затем строим регрессию, в которой за зависимую переменную берется столбец квадратов остатков еi2, а за зависимые переменные –переменные Х1,

Х2, Х3, Х4, Х5, Х6.

Результат представлен на рис. 3.18.

Рис. 3.18. Вывод остатка регрессии

Найдена статистика (3.6): Χ2набл = nR2 = 25 0,68 =17,15 .

Так как Х2набл=17,15> Х2крит =12,59, то гипотеза о гомоскедастичности отвергается и модель считается гетероскедастичной.

Критическое значение распределения Хи-квадрат найдено с помощью действий: fx→Статистические→ХИ2ОБР(m), где m – число переменных, входящих в уравнение регрессии (в данном случае 6).

Тест Вайта (White)

Этот тест аналогичен тесту Бреуша-Пагана. В качестве независимых переменных используются все регрессоры, их квадраты и попарные

произведения.

si2=γ0+γ1xi1+γ2xi2+…+γkxik+ γk+1xi1 xi2+ γk+2xi1 xi3 +…+ γmxik2.

Этапы тестирования:

1.Рассчитывают МНК-оценки коэффициентов регрессии.

2.Находят остатки ei.

3.Находят квадраты остатков ei2.

4.Находят оценку остаточной дисперсии Sˆ 2 .

5.Рассчитывают R2 для регрессии

7.Если X2набл превосходит критическое значение статистики Хи-квадрат для m степеней свободы, то гетероскедастичность присутствует.

Задача 8

По данным таблицы 3.2 проверить гипотезу о гетероскедастичности, используя тест Вайта.

Решение

Так как число переменных, входящих в уравнение не может быть больше 16, оставим только первые четыре переменных. В таблице построим данные, соответствующие квадратам переменных и их перекрестным произведениям (рис. 3.19).

Рис. 3.19. Данные для построения регрессии

Построим уравнение регрессии для этих переменных. Получим коэффициент детерминации, равный 0,98 (рис. 3.20).

Рис. 3.20. Расчет теста Вайта

Рассчитаем статистику по формуле (3.7).

Так как X2набл = nR2=24,64 > Х2крит =22,36 для числа степеней свободы, равного 13, то гипотеза о гомоскедастичности отвергается и модель можно считать гетероскедастичной.

3.5.2. Коррекция на гетероскедастичность

Рассмотрим модель:

yi = β0 + β1 xi +ui .

Пусть ошибки ui не коррелированны, но характеризуются разной дисперсией:

Формула обобщенного метода наименьших квадратов

b = (X T Ω−1 X )−1 X T Ω−1Y

сводится к взвешенному методу наименьших квадратов, так как матрица

Если s2i – известны, то получить модель с гомоскедастичными остатками можно, использовав в качестве весов наблюдений величины 1/σi .

Разделим каждую строку матрицы данных на σi:

В результате получим преобразованную модель:

Заметим, что модель (3.10) не включает свободный член, bi –

коэффициент регрессии при новой переменной h.

На практике дисперсии ошибок почти никогда не известны.

Однако, иногда можно предположить, что σ2i пропорциональны некоторой переменной Zi.

yi = β0 + β1 xi +ui

D ui = σi2

σi = λZi .

Тогда в качестве весов наблюдений следует использовать величину 1/zi:

преобразование для того, чтобы добиться гомоскедастичности удается не всегда.Часто гетероскедастичность является сигналом о неправильной функциональной форме модели.

В общем случае для коррекции гетероскедастичности используют следующую процедуру:

9.Полученные веса wi используют во взвешенном методе наименьших квадратов.

Задача 9

Для регрессии, рассчитанной по таблице 3.2 сделать коррекцию на гетероскедастичность.

Решение

Регрессия, рассчитанная в задаче 5 имеет вид:

уˆ = −0,6423−0,0005x1 +0,000043x2 +0,01858х3 + +0,00133х4 −0,0014х5 +0,00022х6.

Модель гетероскедастична согласно тесту Бреуша-Пагана (задача 7). Возможно, что модель имеет неправильную форму.

Построим модель

logY = β0 +log β1 X1 + β2 log X 2 +... + βk log X k +ε

и модель

logY = β0 + β1 X1 + β2 X 2 +... + βk X k +ε .

Проверим для каждой гипотезу о гетероскедастичности тестом БреушаПагана. Проделайте это самостоятельно, для нахождения логарифмов воспользуйтесь функцией: fx→Математические→LOG.

Сделаем коррекцию на гетероскедастичность, используя взвешенный метод наименьших квадратов.

Рассчитываем МНК-оценки коэффициентов регрессии, найдем остатки ei (не забудьте при нахождении регрессии поставить флажок «Остатки» в параметрах Регрессии).

Найдем квадраты остатков ei2, логарифмы квадратов остатков ln(ei2)

(рис.3.21).

Рис. 3.21. Нахождение логарифмов квадратов остатков

Построим регрессию от логарифмов остатков, независимые

переменные – значения Х1, Х2, Х3, Х4, Х5, Х6.

ln(ei2) = γ0+γ0zi1+γ0zi2+…+γ0zik+ui.

Найдем прогноз ln(ei2)пр и веса наблюдений wi = exp(ln(ei2 прогноз )) (рис.

3.22).

Рис. 3.22. Нахождение весов wi

Рассчитанные веса wi используют во взвешенном методе наименьших квадратов.

Преобразуем имеющиеся по условию данные. Поделим каждое значение таблицы на соответствующие веса, при этом по строке деление на вес не меняется, а по столбцу – меняется. Не забудьте клавишу F4 - при необходимости нажмите на нее два или три раза.

Получим преобразованные данные рис. 3.23 (обратите внимание на строку формул). Дополнительно необходимо построить столбец 1/Вес.

Рис. 3.23. Преобразование данных

Построим регрессию без свободного члена. Для этого в окне «Константа-ноль» поставьте флажок.

Получим результаты регрессии (рис. 3.24). Это модель гомоскедастична, ее коэффициенты имеют ту же самую интерпретацию, а стандартные ошибки более точные:

уˆ′= −0,618 1 −0,00036x1′ +0,0x2′ +0,018х3′ + wi

+0,0014х4′ −0,0014х5′ −0,00026х6′.

Как видно из модели значения коэффициентов поменялось незначительно, однако переменная х5 стала значимой, а х6 – поменяла знак.

Рис. 3.24. Регрессия, построенная взвешенным МНК

На значение коэффициента детерминации при взвешенном МНК обращать внимание не следует.