
тесты для стомата за год
.doc
|
Биомеханика |
|
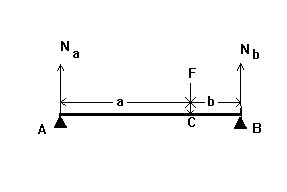
1 a = 4 см, а b = 2 см .Cила реакции опорного зуба А равна
1) 100 Н 2) 200 Н 3) 300 Н 4) 400 Н 5) 500 Н
|
|
2. На рисунке схематично представлен мостовидный протез с двумя двусторонними опорами на естественные зубы A и B. Сосредоточенная сила F равная 720 Н приложена в точке C. a = 4 см, а b = 2 см .Cила реакции опорного зуба В равна
1) 100 Н 2) 250 Н 3) 300 Н 4) 480 Н 5) 580 Н
|
|
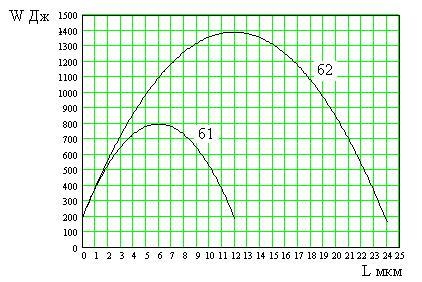
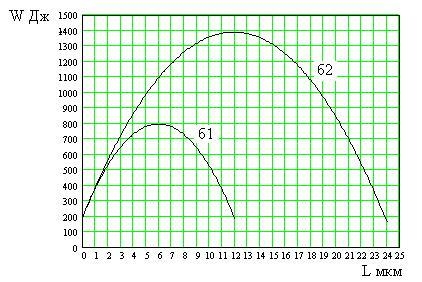
3. На рисунке представлены графики зависимости потенциальной энергии W [Дж]
от длины трещины при двух напряжениях: 0,2 МПа и 0,6 МПа. Образец находится под действием напряжения 0,6 МПа. Минимальная длина трещины, начиная с которой она будет расти равна
1) 8 мкм 2) 15 мкм 3) 16 мкм 4) 20 мкм 5) 40 мкм
|
|
4. На рисунке представлены графики зависимости потенциальной энергии W [Дж] образца от длины трещины при двух напряжениях: 0,2 МПа и 0,6 МПа.
Образец находится под действием напряжения 0,2 Мпа. Максимальная длина трещины, начиная с которой она не будет расти равна 1) 8 мкм 2) 15 мкм 3) 16 мкм 4) 20 мкм 5) 40 мкм
|
|
5. На рисунке представлены графики зависимости потенциальной энергии W [Дж] образца от длины трещины при двух напряжениях: 0,2 МПа и 0,6 МПа.
Образец находится под действием напряжения 0,2 Мпа. Минимальная длина трещины, начиная с которой она будет расти равна 1) 8 мкм 2) 15 мкм 3) 16 мкм 4) 20 мкм 5) 40 мкм
|
|
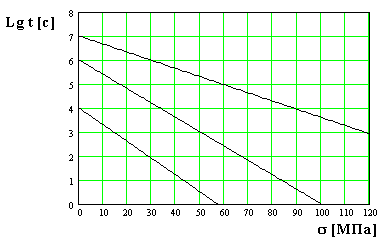
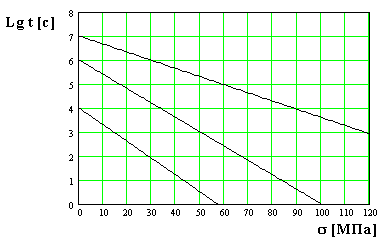
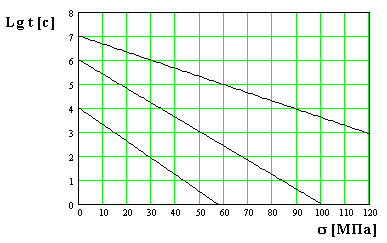
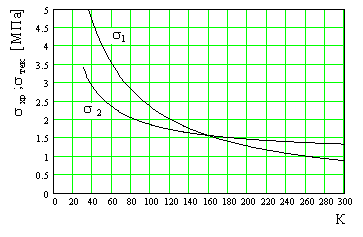
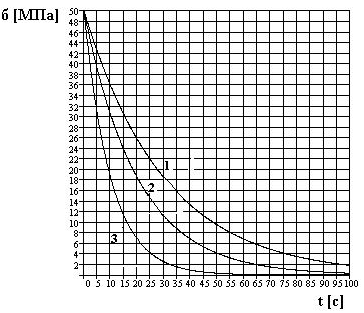
6. На рисунке представлена зависимость логарифма долговечности материала от напряжения
при различных температурах: 350 К, 300 К, 250 К . Долговечность материала при температуре 250 К и механическом напряжении 90 МПа равна (с) 1) 10 2 2) 10 3 3) 10 4 4) 10 5 5) 10 6
|
|
7. На рисунке представлена зависимость логарифма долговечности материала от напряжения при различных температурах: 350 К, 300 К, 250 К
Долговечность материала при температуре 250 К и механическом напряжении 30 МПа равна (с) 1) 10 2 2) 10 3 3) 10 4 4) 10 5 5) 10 6
|
|
8. На рисунке представлена зависимость логарифма долговечности материала от напряжения при различных температурах: 350 К, 300 К, 250 К
Долговечность материала при температуре 300 К и механическом напряжении 50 МПа равна (с) 1) 10 2 2) 10 3 3) 10 4 4) 10 5 5) 10 6
|
|
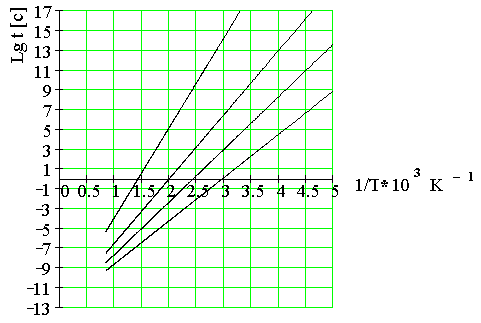
9. На рис. представлены температурные зависимости логарифма долговечности образцов материала для базисов протезов при различных напряжениях: 1 МПа, 2 МПа, 3 МПа, 5 МПа
Долговечность образца, находящегося под напряжением 3 МПа при температуре 60 0 С равна 1) 1 с 2) 10 с 3) 10 3 с 4) 10 5 с 5) 10 7 с
|
|
10. На рис. представлены температурные зависимости логарифма долговечности образцов при различных напряжениях: 1 МПа, 2 МПа, 3 МПа, 5 МПа
Долговечность образца, находящегося под напряжением 1 МПа при температуре 227 0 С. 1) 1 с 2) 10 с 3) 10 3 с 4) 10 5 с 5) 10 7 с
|
|
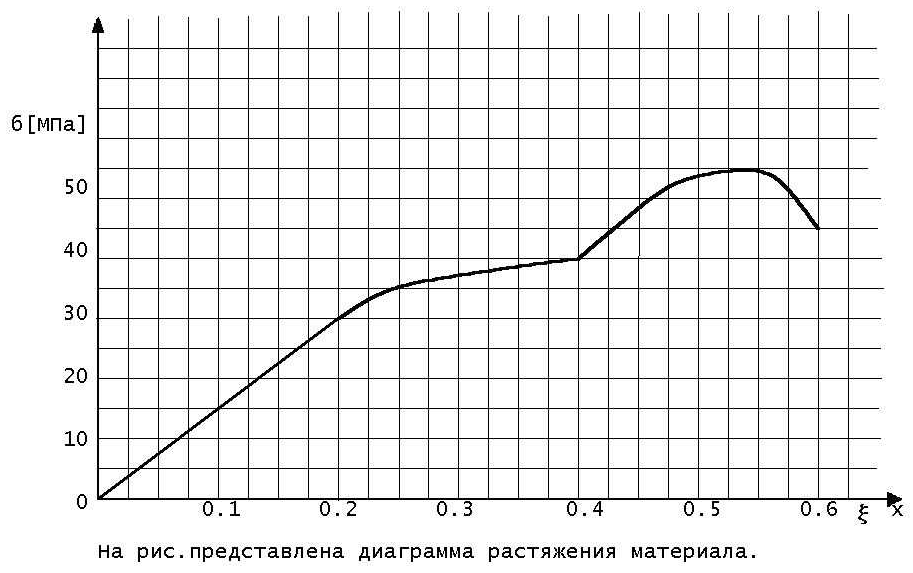
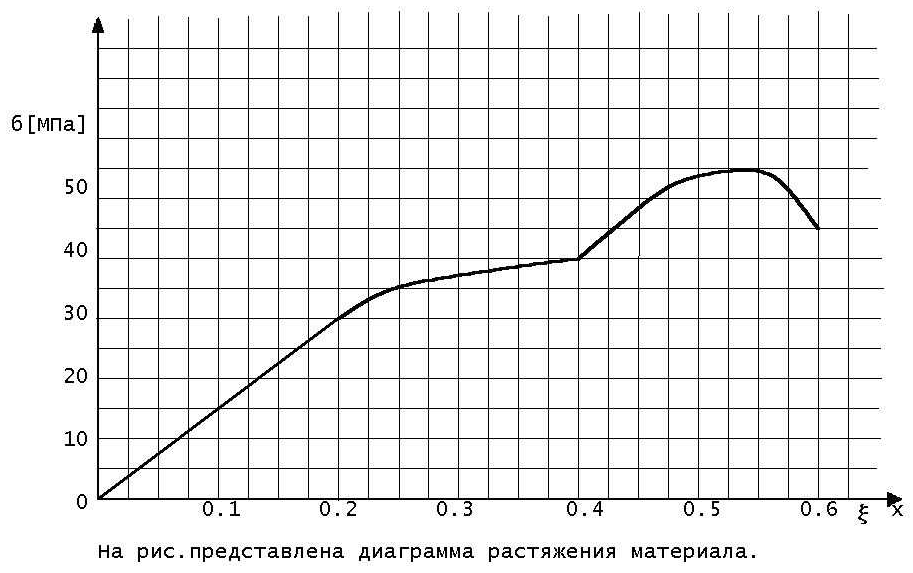
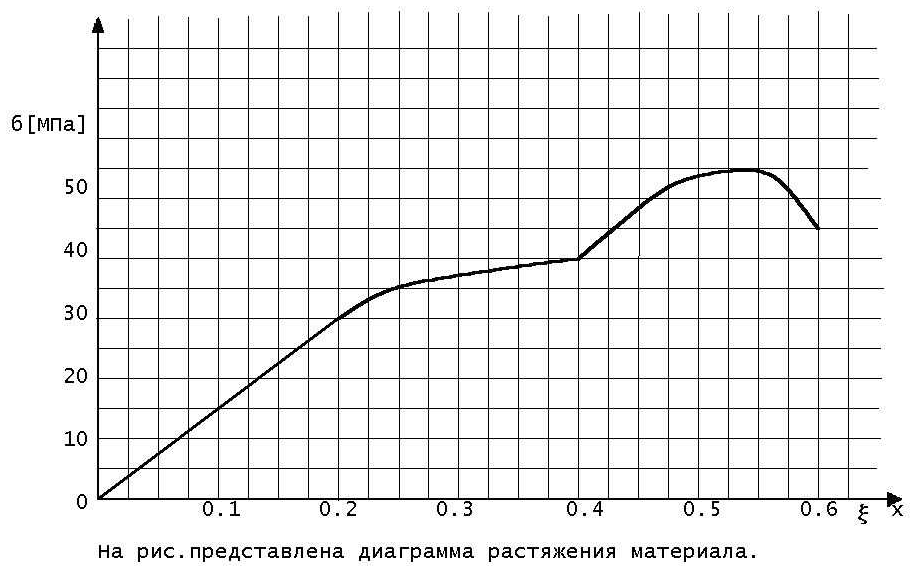
11.
При этом модуль упругости материала больше предела прочности. 1) в 1,5 раза 2) в 2 раза 3) в 2,5 раза 4) в 2,7 раза 5) в 3 раза
|
|
12.
Образец при разрыве растянулся 1) в 1,2 раза 2) в 1,4 раза 3) в 1,6 раза 4) в 1,8 раза 5) в 2 раза
|
|
13.
Модуль упругости материала равен 1) 30 МПа 2) 60 МПа 3) 90 МПа 4) 120 МПа 5) 150 МПа
|
|
14.
Конечная длина образца при разрыве 32 см. Его начальная длина равна. 1) 10 см 2) 15 см 3) 20 см 4) 25 см 5) 30 см
|
|
15.
Начальная длина образца 10 см. Он разорвался при конечной длине равной 1) 0,6 см 2) 5 см 3) 10 см 4) 15 см 5) 16 см |
|
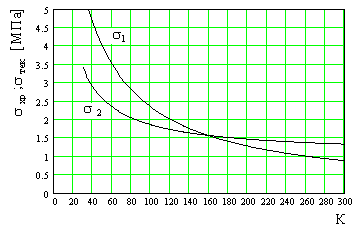
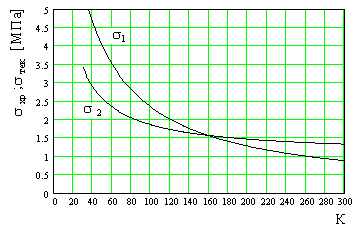
16. На рисунке даны зависимости пределов хрупкой прочности и текучести от температуры.
Предел текучести при температуре 60 К равен 1) 1 МПа 2) 2 МПа 3) 3 МПа 4) 3,5 МПа 5) 4,5 МПа
|
|
17. На рисунке даны зависимости пределов хрупкой прочности и текучести от температуры
Разрушение у образца при температуре 200 K будет 1) хрупкое 2) пластическое
|
|
18. На рисунке даны зависимости пределов хрупкой прочности и текучести от температуры
Разрушение у образца при температуре 100 K будет 1) хрупкое 2) пластическое
|
|
19. На рисунке даны зависимости пределов хрупкой прочности и текучести от температуры
Предел хрупкой прочности при температуре 80 К равен 1) 1 МПа 2) 2 МПа 3) 3 МПа 4) 3,5 МПа 5) 4,5 МПа
|
|
20. На рисунке даны зависимости пределов хрупкой прочности и текучести от температуры
Максимальная температура, при которой образец хрупко разрушается равна 1) 40 К 2) 60 К 3) 120 К 4) 160 К 5) 300 К
|
Гемодинамика и биореология
|
21. Объемная скорость кровотока при переходе от участка сосудистого русла с общей площадью поперечного сечения S(1) = 150 мм 2 к участку сосудистого русла с общей площадью поперечного сечения S(2) = 900 мм 2 изменяется 1) в 6 раз 2) в 4 раза 3) в 3 раза 4) в 2 раза 5) в 1 раз
|
|
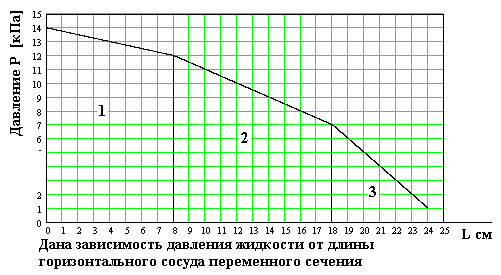
22.
Отношение гидравлических сопротивлений на участках 2 и 1 равно 1) 1 2) 2 3) 2,5 4) 3 5) 3,5
|
|
23.
Отношение гидравлических сопротивлений на участках 2 и 3 равно
1) 1 2) 5/6 3) 5/3 4) 5/2 5) 3
|
|
24.
Отношение гидравлических сопротивлений на участках 3 и 1 равно 1) 1 2) 2 3) 2,5 4) 3 5) 3,5
|
|
25. При увеличении скорости кровотока в 2 раза, увеличении радиуса сосуда в 2 раза и уменьшении вязкости крови в 10 раз число Рейнольдса. 1) Увеличится в 40 раз 2) Увеличится в 0,4 раза 3) Не изменится 4) Уменьшится в 0,4 раза 5) Уменьшится в 10 раз.
|
|
26. Напряжение в упругом элементе модели упруговязкого тела составляет 19 Па. Модуль упругости упругого элемента равен 1 Па, коэффициент динамической вязкости ньютоновского элемента равен 0,13 Пас , Напряжение в вязком элементе равно 1) 9 Па; 2) 13 Па; 3) 19 Па; 4) 29 Па; 5) 32 Па
|
|
27. При уменьшении радиуса просвета кровеносного сосуда в 2 раза и увеличении вязкости крови в 1,5 раза гидравлическое сопротивление. 1) Уменьшилось в 24 раза 2) Уменьшилось в 16 раз 3) Уменьшилось в 9 раз 4) Увеличилось в 9 раз 5) Увеличилось в 24 раза
|
|
28. Общее гидравлическое сопротивление 3 одинаковых параллельных кровеносных сосудов с гидравлическим сопротивлением одного из них равным – Х будет равно 1) 9 Х 2) 3 Х 3) Х/2 4) Х/3 5) Х/9
|
|
29. При использовании кессоновской модели реологического поведения крови асимптотическая вязкость равна 1) кессоновской вязкости; 2) половине значения кессоновской вязкости 3) квадрату значения кессоновской вязкости; 4) корню квадратному из значения кессоновской вязкости; 5) пределу текучести крови.
|
|
30. Относительная деформация упругого элемента вязкоупругой системы равна 0,9. Модуль упругости упругого элемента равен 2 Па, а коэффициент вязкости вязкого элемента равен 2 мпас, относительная деформация вязкого элемента при этом равна 1) 0,2 2) 1 3) 0,9 4) 2,9 5) 4
|
|
31. Для ньютоновской жидкости, при касательном напряжении 5 Па и скорости сдвига 20 с – 1, коэффициент динамической вязкости равен 1) 0,60 Пас 2) 0,30 Пас 3) 0,25 Пас 4) 0,10 Пас 5) 0,05 Пас
|
|
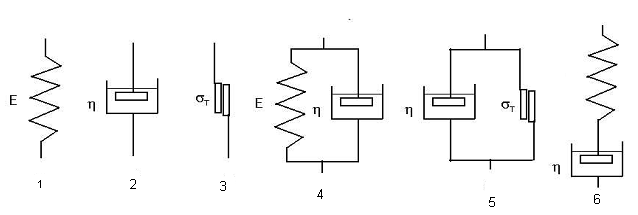
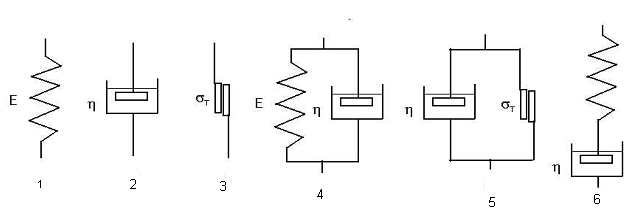
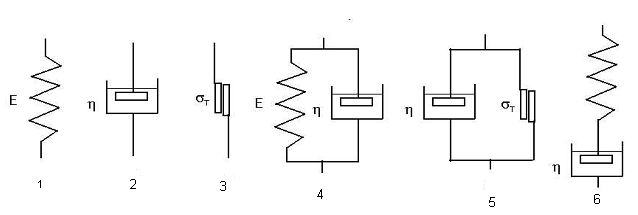
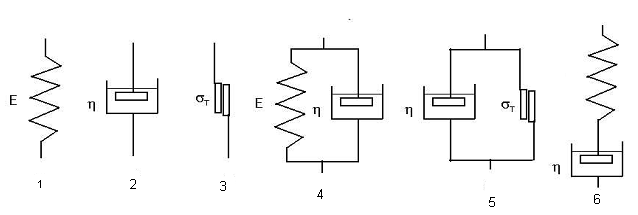
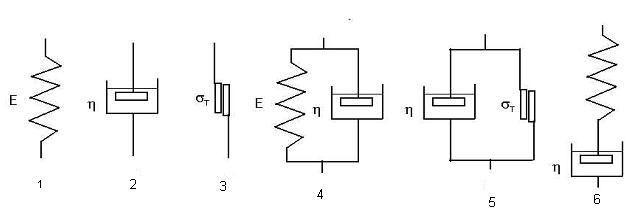
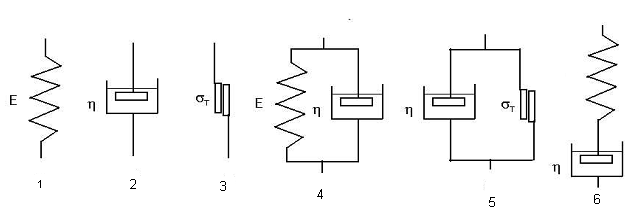
32. Укажите номер модели, описывающей вязкоупругие свойства материалов.
|
|
33. Укажите номер модели, описывающей идеально-упругие свойства материалов.
|
|
34. Укажите номер модели, описывающей идеально-вязкие свойства материалов.
|
|
35. Укажите номер модели, описывающей упруго-вязкие свойства материалов.
|
|
36. Укажите номер модели, описывающей идеально-пластичные свойства материалов.
|
|
37. Укажите номер модели, описывающей вязко-пластичные свойства материалов.
|
|
38.
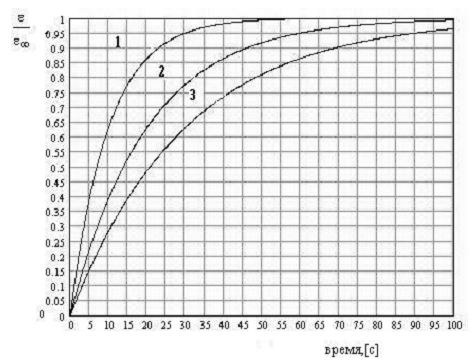
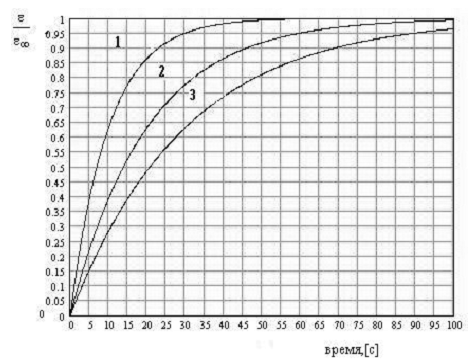
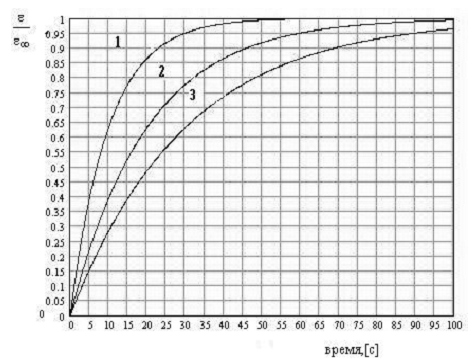
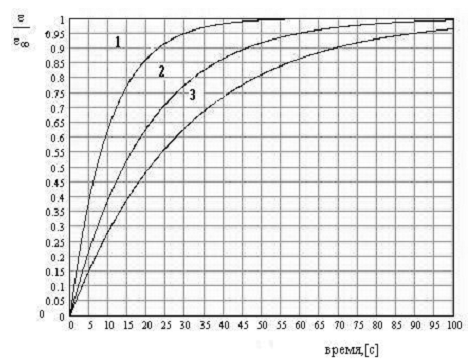
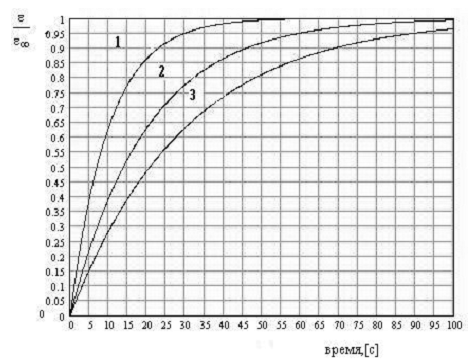
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для первого материала, модуль упругости которого равен Е = 10 Па, коэффициент вязкости равен 1) 100 Па*с 2) 200 Па*с 3) 300 Па*с 4) 400 Па*с 5) 600 Па*с
|
|
39.
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для второго материала, модуль упругости которого равен Е = 20 Па, коэффициент вязкости равен 1) 100 Па*с 2) 200 Па*с 3) 300 Па*с 4) 400 Па*с 5) 600 Па*с
|
|
40. На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Время релаксации для второго материала равно
1) 5 с 2) 10 с 3) 15 с 4) 20 с 5) 30 с
|
|
41.
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для третьего материала, модуль упругости которого равен Е = 20 Па, коэффициент вязкости равен 1) 100 Па*с 2) 200 Па*с 3) 300 Па*с 4) 400 Па*с 5) 600 Па*с
|
|
42.
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для первого материала, коэффициент вязкости которого равен η = 40 Па*с , модуль упругости равен 1) 1 Па 2) 2 Па 3) 3 Па 4) 4 Па 5) 6 Па
|
|
43.
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для второго материала, коэффициент вязкости которого равен η = 100 Па*с , модуль упругости равен 1) 1 Па 2) 2 Па 3) 3 Па 4) 5 Па 5) 6 Па
|
|
44. .
На рис. даны кривые ползучести различных материалов, отличающихся временами релаксации. Для третьего материала, коэффициент вязкости которого равен η = 90 Па*с , модуль упругости равен 1) 1 Па 2) 2 Па 3) 3 Па 4) 4 Па 5) 6 Па
|
|
45.
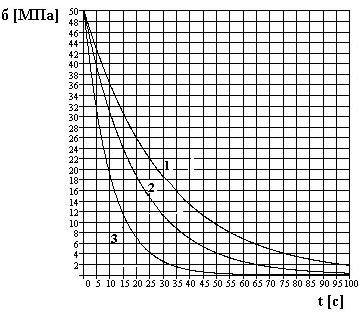
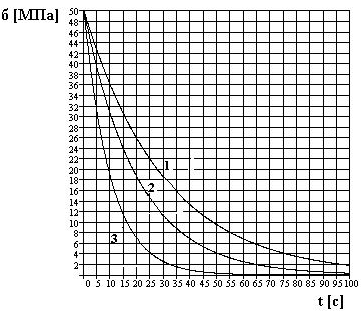
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Время релаксации для второго материала равно 1) 10 с 2) 20 с 3) 30 с 4) 40 с 5) 50 с
|
|
46.
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Время релаксации для первого материала равно 1) 10 с 2) 20 с 3) 30 с 4) 40 с 5) 50 с
|
|
47.
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Для первого материала, модуль упругости которого равен E = 10 Па, коэффициент вязкости равен 1) 100 Па*с 2) 200 Па*с 3) 300 Па*с 4) 400 Па*с 5) 600 Па*с
|
|
48.
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Для второго материала, модуль упругости которого равен E = 20 Па, коэффициент вязкости равен 1) 100 Па*с 2) 200 Па*с 3) 300 Па*с 4) 400 Па*с 5) 600 Па*с
|
|
49.
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Для первого материала, коэффициент вязкости которого η = 120 Па*с, модуль упругости Е равен 1) 1 Па 2) 2 Па 3) 3 Па 4) 4 Па 5) 5 Па
|
|
50.
На рис. Представлены кривые релаксации напряжения для трех различных материалов. Для третьего материала, коэффициент вязкости которого η = 50 Па*с, модуль упругости Е равен 1) 1 Па 2) 2 Па 3) 3 Па 4) 4 Па 5) 5 Па
|
|
Биоакустика |
|
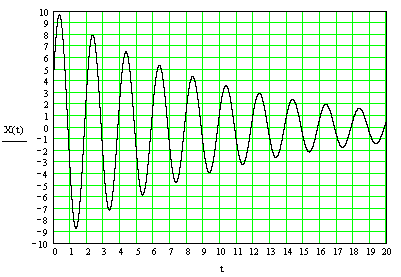
51. На рис представлен график затухающих колебаний. Х = А * exp (- * t) cos( * t + 0)
1) π 2) π/2 3) π/3 4) - π/3 5) – π
|
|
52. На рис представлен график затухающих колебаний
Период колебаний равен 1) 1 с 2) 2 с 3) 3 с 4)5 с 5) 10 с
|
|
53. На рис представлен график затухающих колебаний
Частота колебаний равна 1) 0,1 Гц 2) 0,5 Гц 3) 1 Гц 4) 2 Гц 5) 4 Гц
|
|
54. На рис представлен график затухающих колебаний.
Круговая частота колебаний равна 1) 2,72 1/с 2) 3,14 1/с 3) 4,12 1/с 4) 6,28 1/с 5) 12,56 1/с
|
|
55. Период колебаний определяется как 1) Число колебаний в единицу времени 2) Время наблюдения процесса колебаний. 3) Время одного полного колебания. 4) Число колебаний за время течения данного процесса
|
|
56. Уравнение колебаний имеет вид: Х + 8 Х + 16 Х = 10 cos ( 8 t ) . Коэффициент затухания равен 1) 4 с - 1 2) 8 с - 1 3) 16 с -1 4) 8 с 5) 4 с
|
|
57. Маятник совершает гармонические колебания по закону косинуса, начало отсчета времени совпало с моментом прохождения маятником положения максимального отклонения от положения равновесия, начальная фаза колебаний при этом равна 1) 6,28 2) 3,14 3) 1,56 4) 0,5 5) 0
|
|
58. Гармонические колебания материальной точки массой 7 г происходят по закону: x = 5 COS( 27 t +12) t - в секундах; x - в миллиметрах. Круговая частота изменения потенциальной энергии при этом равна 1) 27 1/с 2) 35 1/с 3) 54 1/с 4) 135 1/с 5) 314 1/с
|
|
59. Гармонические колебания материальной точки массой 7 г происходят по закону: x = 8 COS( 20 t +12) t - в секундах; x - в миллиметрах. Круговая частота изменения кинетической энергии при этом равна 1) 20 1/с 2) 40 1/с 3) 54 1/с 4) 135 1/с 5) 314 1/с
|
|
60 . Гармонические колебания материальной точки массой 7 г происходят по закону: x = 10 COS( 20 t +12) t - в секундах; x - в миллиметрах. Круговая частота изменения полной энергии при этом равна 1) 0 1/с 2) 20 1/с 3) 70 1/с 4) 135 1/с 5) 314 1/с
|
|
61.При неизменной частоте энергия гармонических колебаний возросла в 4 раз. Амплитуда колебаний при этом изменилась 1) в 4 раза 2) в 3,14 раза 3) в 2 раза 4) в 1,56 раза 5) в 0 раз
|
|
62. Правильно укажите типы колебаний. 1) Звуковые. 2) Свободные. 3) Электромагнитные. 4) Вынужденные. 5) Механические. 6) Автоколебания 7) Параметрические
|
|
63. При постоянной интенсивности звука частота увеличилась в два раза. Амплитуда колебаний при этом 1) уменьшилась в 4 раза 2) уменьшилась в 2 раза 3) не изменилась 4) возросла в 2 раза 5) возросла в 4 раза
|
|
64. Продольными волнами называются те, в которых 1) колебания происходят перпендикулярно скорости распространения волны. 2) колебания происходят вдоль выбранного в пространстве направления. 3) смещения подчиняются закону косинуса или синуса. 4) колебания происходят параллельно скорости распространения волны.
|
|
65. Если частота и скорость распространения волны увеличились в 3 раза, то величина модуля вектора Умова 1) Увеличилась в 27 раз 2) Увеличилась в 9 раз. 3) Увеличилась в 3 раза. 4) Не изменилась. 5) Уменьшилась в 9 раз.
|
|
66. Частота гармоник равна 1) Произвольному значению, превышающему основную частоту. 2) Произвольному значению меньшему, чем основная частота. 3) Она кратна значению основной частоты. 4) Любому значению.
|
|
67. Неподвижный приемник регистрирует звук от приближающегося к нему источнику. При этом, если регистрируемая частота равна половине частоты источнику, то скорость источника при этом 1) 0 м/с 2) 10 м/с 3) З40 м/c 4) Такого быть не может.
|
|
68. При различии в уровнях интенсивностей звука равном 30 дБ, отношение интенсивности равно 1) 10 . 2) 30 3) 100 4) 1000 5) 10000
|
|
69. Какие Из перечисленных методов диагностики к звуковой не относятся 1) Шумометрия. 2) Фонокардиография. 3) Перкуссия. 4) Аускультация. 5) Аудиометрия. 6) Кардиография. 7) УЗИ.
|
|
70. Сила звука это 1) Энергия продольной звуковой волны. 2) Энергия волны, проходящая в единицу времени через единицу площади. 3) Давление звука на единицу площади. 4) Это громкость звука. 5) Сила давления на барабанную перепонку
|
|
71. Громкость звука это 1) Его интенсивность. 2) Сила давления на барабанную перепонку. 3) Энергия звука. 4) Степень слухового ощущения данного звука. 5) Давление звука на единицу площади.
|
|
72. Укажите величину отношения болевого порога к порогу слышимости. 1) 10 5 2) 10 7 3) 10 9 4) 10 13 5) 10 15
|
|
73. Если интенсивность звука частотой 100Гц возросла с 10 - 8 Вт/ м2 до 10 - 2 Вт/ м2 , то уровень громкости звука в фонах изменился на 1) 20 2) 30 3) 40 4) 50 5) 60
|
|
74.
Н
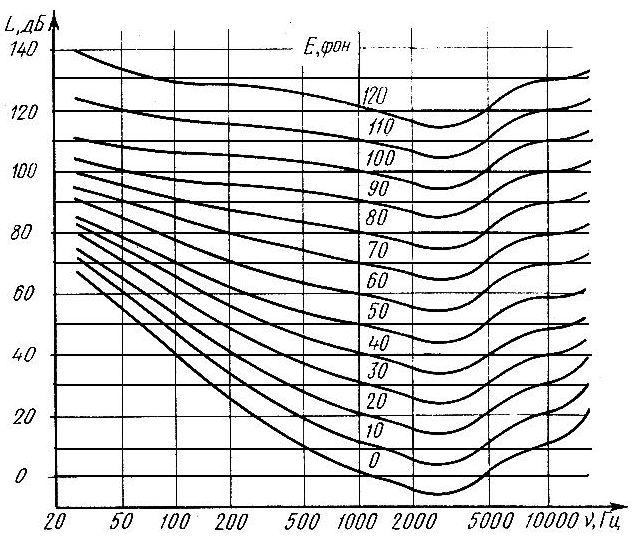
Определить уровень громкости на частоте 500 Гц при его уровне интенсивности 20 дБ. 1) 10 фон 2) 20 фон 3) 30 фон 4) 40 фон 5) 50 фон
|
|
75.
Н
Определить уровень громкости на частоте 50 Гц при его уровне интенсивности 70 дБ. 1) 10 фон 2) 20 фон 3) 30 фон 4) 40 фон 5) 50 фон
|
|
76. .
Н
Определить уровень громкости на частоте 200 Гц при его уровне интенсивности 40 дБ. 1) 10 фон 2) 20 фон 3) 30 фон 4) 40 фон 5) 50 фон
|
|
77. .
Н
Определить уровень громкости на частоте 100 Гц при его уровне интенсивности 60 дБ. 1) 10 фон 2) 20 фон 3) 30 фон 4) 40 фон 5) 50 фон
|
|
78.
Н
Определить уровень интенсивности на частоте 200 Гц при его уровне громкости 20 фон 1) 10 дБ 2) 20 дБ 3) 30 дБ 4) 40 дБ 5) 50 дБ
|
|
79.
Н
Определить уровень интенсивности на частоте 200 Гц при его уровне громкости 70 фон 1) 10 дБ 2) 20 дБ 3) 30 дБ 4) 50 дБ 5) 80 дБ
|
|
80. Н
Определить уровень интенсивности на частоте 500 Гц при его уровне громкости 10 фон 1) 10 дБ 2) 20 дБ 3) 30 дБ 4) 40 дБ 5) 50 дБ
|

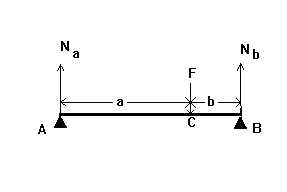 На рисунке схематично представлен
мостовидный протез с двумя двусторонними
опорами на естественные зубы A и B.
Сосредоточенная сила F равная 900 Н
приложена в точке C.
На рисунке схематично представлен
мостовидный протез с двумя двусторонними
опорами на естественные зубы A и B.
Сосредоточенная сила F равная 900 Н
приложена в точке C.













 Начальная фаза колебаний, при этом
равна
Начальная фаза колебаний, при этом
равна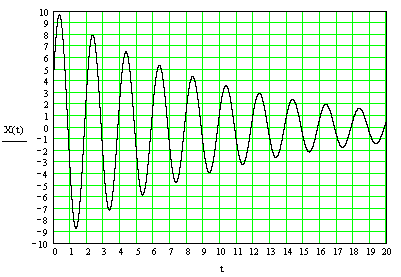

 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.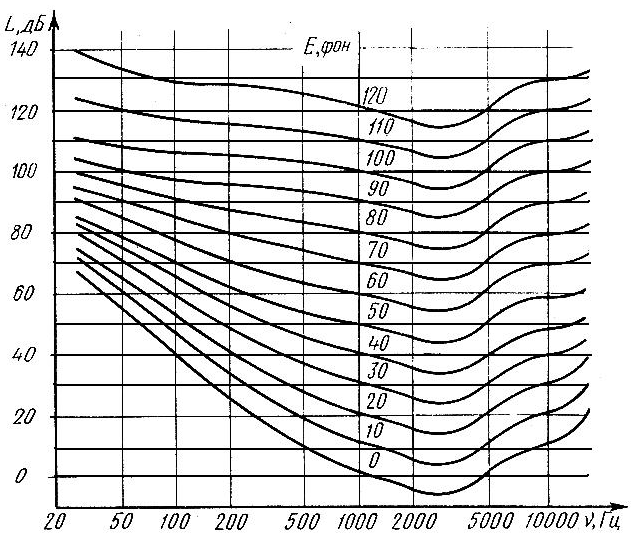 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.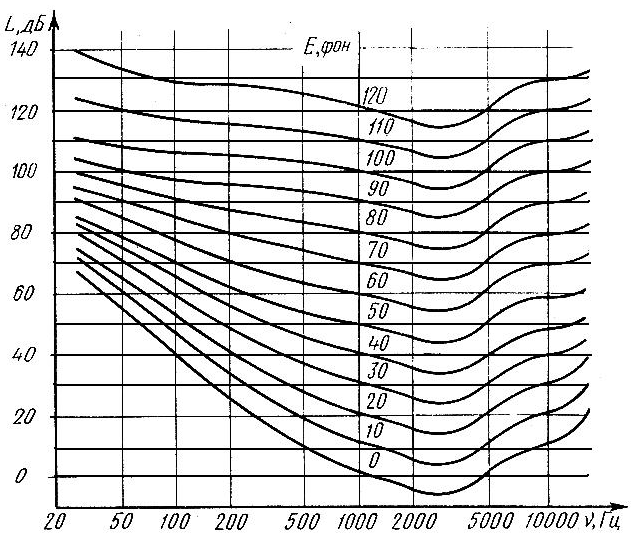 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.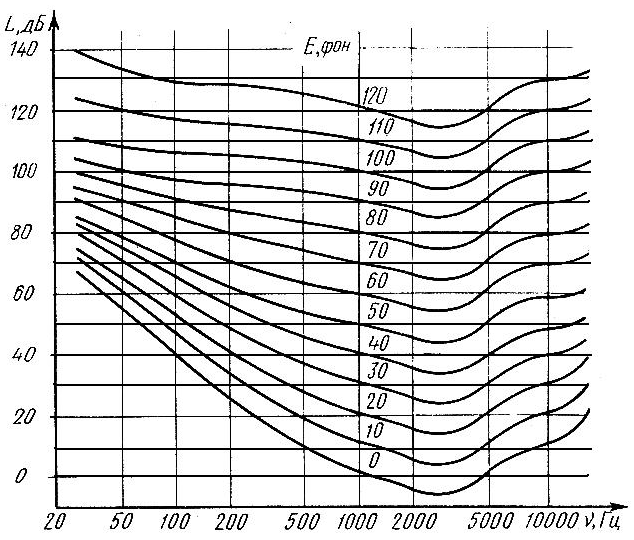 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.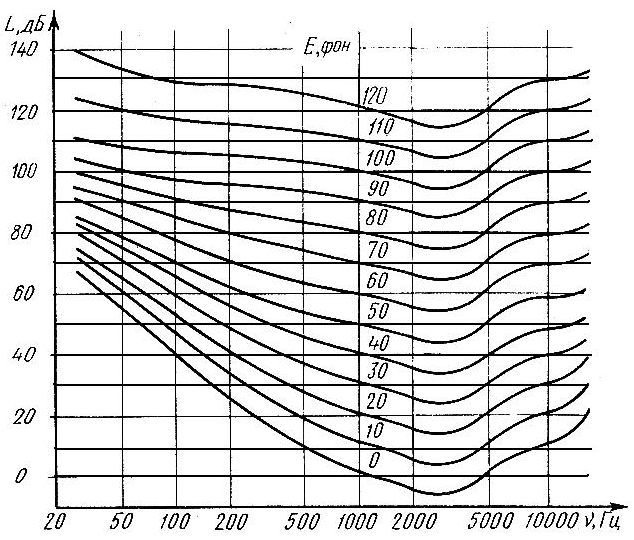 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.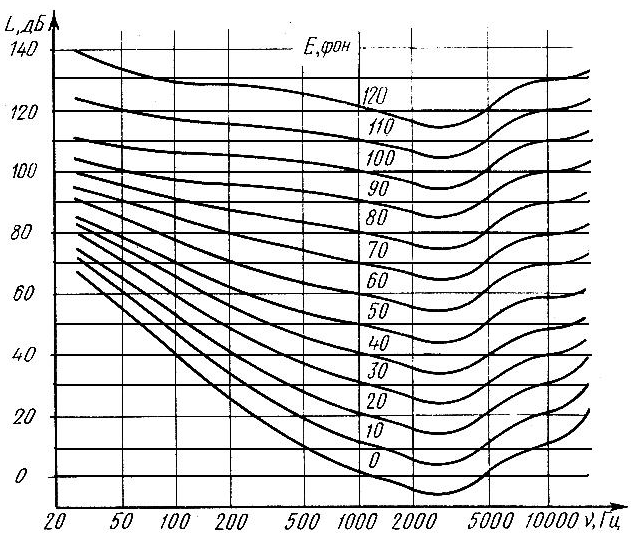 а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости. а
рис. Представлены кривые равной
громкости.
а
рис. Представлены кривые равной
громкости.